物元法分类动态综合评价方法及速度特征分析
2015-06-01廖志高徐玖平
廖志高,詹 敏,徐玖平
(1.广西科技大学管理学院,广西 柳州 545006;2.四川大学商学院,四川 成都 610064)
物元法分类动态综合评价方法及速度特征分析
廖志高1,詹 敏1,徐玖平2
(1.广西科技大学管理学院,广西 柳州 545006;2.四川大学商学院,四川 成都 610064)
针对动态多指标决策问题,提出一种物元法分类动态综合评价方法,并对数据进行速度特征分析提出改进措施。在该方法中,首先将定性和定量因素联系起来进行研究,通过关联度分析,使评价中的问题定量化;然后将数据进行”奖优罚劣”规范化后,从均值和理想点两个角度作为参考,并采用”先进平均数”和”落后平均数”进行分类和动态综合评价;并在此基础上,利用速度特征分析原因并提出改进措施。最后,通过一个算例说明了该方法的有效性和可行性。
物元法;分类;动态综合评价;速度特征分析
1 引言
动态多指标决策是指在决策空间和目标空间的基础上,又增加了时间空间,是包含有时间、指标和方案的三维决策问题,其决策过程与结果具有动态的特点。现有的动态综合评价方法从函数的角度看有如下三种基本评价方式:第一,先将每个时间维度上的数据按指标权重静态综合然后再进行时间维综合。第二,先对各指标数据按时序权重进行集结,然后拟静态综合。第三,构造映射将三维空间的样本直接映射到一维直线上,其映射函数就是总的动态评价函数。常见的动态综合评价方法一般利用动态综合评价原理将好坏矩阵和增减矩阵组合而成,以及其他方法如灰色矩阵法、投影寻踪模型、小波神经网络、构造目标函数、引入速度特征等[1-16]。
其研究思路一般为:(1)确定评价指标,建立指标体系,样本的选取及数据的收集;(2)指标量化,数据的无量纲化和规范化;(3)时间权重和指标权重的取得;(4)综合评价函数的运用等[4-6]。
从国内外已有的文献来看目前关于综合评价方法研究仍存在三个突出的问题[17-18]。第一,多方法评价的非一致性。目前综合评价方法众多,但对于一个复杂对象的评价,不仅受所遴选的专家群及描述被评价对象特征的指标体系的影响,还受所选评价方法的影响,对同一组对象使用不同的评价方法其结论可能存在较大差异。
第二,缺乏分类评价。现有的动态综合评价方法只有对目标方案计算综合评价值和排序而没有进行分类,这将使评价结果不完善甚至使决策者做出错误的决定。比如各个方案虽然均为非劣解且能计算出其综合评价值和对方案进行排名,但所评价的方案可能均不是很理想,即便是第一名或者前几名仍与正理想方案有差距,可能导致决策者做出错误的决策。
第三,现有的评价方法只做评价而没有指出各方案的优势和不足并提供改进点。
物元模型是由我国著名学者蔡文教授首先提出的,该模型能够将定性和定量因素联系起来进行研究,通过关联度分析,使评价中的问题定量化。与其他评价方法不同,物元分析的关联度函数概念将评价取值由传统方法的[0,1]区间延展至(-∞,+∞)区间,由于引入了负数概念的关联度,使评价可以在整个实数范围内进行,不会出现信息丢失,因此保证了各影响因素信息的完整性。
目前基于物元法的评价方法已有很多相关论文,但还没有采用该方法进行动态综合评价的相关文章[19-22]。同时本文借助“奖优罚劣”的优势进行数据规范化,从均值和理想点两个角度分别考虑,并利用“先进平均数”和“落后平均数”进行动态综合评价和分类。由于利用“双标准”其评价分类结果详尽克服了上文中提到的综合评价问题的不足,说服力强;同时利用速度特征对相关数据进行分析和改进,效果显著,适用范围广,实用性强,值得推广。
2 动态综合评价物元法知识简介
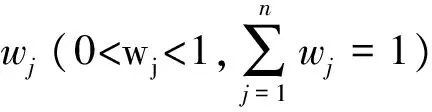
2.1 物元基础知识
在物元分析中,所描述的事物N及其特征C和量值X共同组成物元R = (N,C,X)或R =〔N,C,C(N)〕,以便对事物作定性分析和定量计算。
(1)全征物元。如果一个事物为N,其有n个特征,第j个特征表示为Cj(j=1,2,…,n),其Cj所对应的量值为Xj,则全征物元可表示为:
事物关于某特征的量值,随着时间t(t=1,2,…,l)的变化往往也产生变化,本文以tXj表示物元N其第j个特征在t时刻所对应的特征值,表示为tR=(tN,C,tX),时间t(t=1,2,…,l)。


2.2 特征值的计算或获取
特征值tXij的计算或获取取决于特征值的属性。在解决实际问题时,问题的矛盾程度是由事物关于某个量值符合要求的程度表述的,事物的量值可分为数量值和非数量值,非数量值必须通过数量化变成数量值。关联函数是用来刻画可拓集合的,其取值范围为整个实数轴,所以物元法中的量值便可从此实数轴上取值,这个值为根据关联函数所确定的某一特定值。两事物间的关联性可用关联函数来表示,称其为关联函数,表示为K(x)。在实数域起作用的点和区间,而点与点的距离在经典数学中已有定义,即ρ(x,y)=|x-y|。为了建立关联函数,我们还要定义点与区间的距离,即“距”的概念:设x为实域(-∞,+∞)上的任一点,X0=〈a,b〉为实域上任一区间,称

为x和区间X0之距。
物元矩阵按照各特征值的一般量值范围和最高允许量值范围,一般的设X0=
关联函数可以表示为:
由于关联函数K(x)和隶属函数u(x)中所含的元素为x,均属于中介元,两者的区别仅仅是关联函数较隶属函数多一段有条件可以转化的量值范围。
诚然,将定性指标定量化,t时刻第i(i=1,2,…,m)个事物的第j(j=1,2,…n)个特征对应的特征值可以是精确数和模糊数等,最终需要将数值无量纲化和规范化为tξij。
3 物元法综合评价步骤
3.1 物元特征值规范化处理
针对问题1、2,文章将严格按照动态综合评价的原理,先将原始数据进行关联度分析,接着将关联度数据进行规范化处理再进行静态综合评价和分类,然后对静态综合评价值利用好坏矩阵和增长矩阵进行修正,最后利用多目标函数和理想点法对各物元进行时序综合评价和分类。
由于本文把经典域与节域相互重合,故关联系数可由隶属数值加以确定,于是有Kij=u(Xij)。各单项指标相应的量值从属于最优方案量值的程度,称为从优隶属度。由于各指标的量纲不同,分为效益型、成本型、和区间型指标(固定型可视为区间型的特例)。本文采用“奖优罚劣”的[-1,1]的线性变换进行数据的规范化处理,弥补了[0,1]区间变换只奖不罚的不足,评价结果更易识别,并能体现出均值和理想值,具体做法不再赘述[13]。
3.2 物元静态综合评价

(1.1)
(2)特征指标权重。以Rw表示物元各项特征指标所对应的特征指标权重,其特征指标权重复合物元表示为:
采用层次分析法、熵值法、组合权重法等方法加以确定。
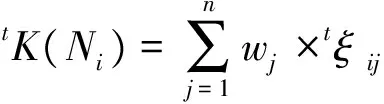
其中tK(Ni)表示t时刻第i个物元的静态综合评价值。计算每一时期的静态综合评价值即可得:
(1.2)
(4)分类评价。在实际操作中一般选取近期较多的样本量作为物元,计算出各指标值的平均值即平均定额标准,再以平均值为参照标准,将大于平均值的物元特征值提出计算“先进平均数”,作为“先进定额标准”,将小于平均值的物元特征值提出,计算“落后平均数”,作为“落后定额标准”,并找出正理想物元和负理想物元以此将样本分为四大类,相关表述如下:
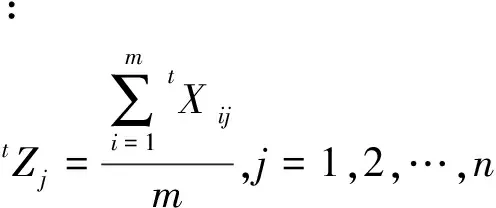
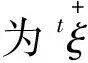
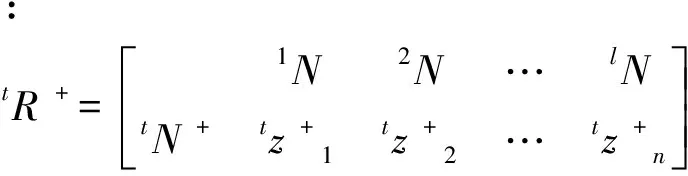
tz+j,tz-j(j=1,2,…,n)分别为第j个特征指标中的正理想值和负理想值。
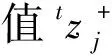

表1 物元t时刻的“五线谱”静态分类标准图
3.3 修正的物元静态综合评价值的计算
为了综合考虑评价特征指标的好坏程度和增长程度,先将静态综合评价值视为好坏矩阵并对其进行时序相减计算好坏矩阵各个时刻的变化值作为增长矩阵,接着对好坏矩阵乘以其权重和增长矩阵乘以其相应的权重进行加和,作为修正的物元各时序的静态综合评价值。
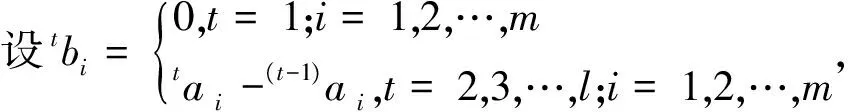
其中tai为静态综合值,tbi为tai的时序相减变化值,tci为修正的物元静态综合评价值。α,β表示好坏矩阵与增长矩阵的相对重要程度,0<α<1,0<β<1,α+β=1。tbi的意义是,若tbi>0表示对指标好坏程度的一种奖励,若tbi<0表示对指标好坏的惩罚。以下用cij组成的矩阵利用理想点法构造正理想时序数和负理想时序数C+=(1C+,2C+,…,lC+),C-=(1C-,2C-,…,lC-),
tC+=max{tCi|i=1,2,…,m},t=1,2,…,ltC-=min{tCi|i=1,2,…,m},t=1,2,…,l
最后对ci进行时序综合评价和分类。
3.4 理想物元法时序动态综合评价和分类
为了更加科学合理的对物元进行综合评价,现考虑时间序列构成动态综合评价。根据待评价物元与正负理想物元的距离,用多目标函数确定各物元的时序动态综合评价值进行评价和分类。
(1)计算待评物元至理想点的距离。若以Rd+、Rd-分别表示距正理想物元和距负理想物元,Zd+、Zd-分别表示为距正理想物元的距离和距负理想物元的距离,则采用加权平均处理得:
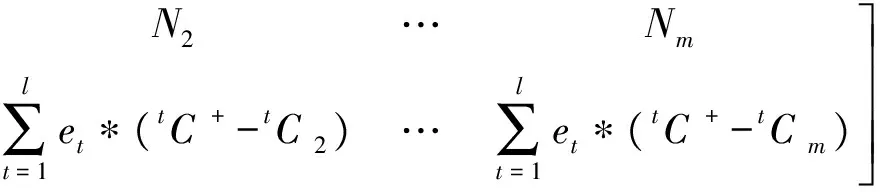
(2)时序动态综合评价值计算。先建立目标函数,然后求其最小二乘解。设物元的目标函数为G(ki),其中ki为实函数,在实数域内“距离的平方和最小”,若将其扩展为“时序权距离平方和最小”仍然适用,因而有:
上式ki为待定值,对每一个ki均可求导,令其为零,即dF(ki)/dki=0,得

以此可建立m个事物的关联复合物元为:
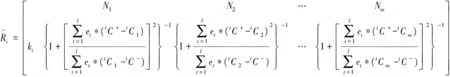
(3)综合值分类评价。
将正理想点、先进平均数、均值、落后平均数及负理想点的静态评价值也分别求其与正理想点和负理想点的距离计算时序动态综合值,分类表与表1 相似。根据计算的ki值进行排序、分类动态综合评价,动态综合评价值越大分类越靠前表明其越接近最优值,从而确定决策对象。
4 评价结果分析及原因分析
针对问题3,本文引入速度特征这一物理意义来解决,具体方法如下。先将静态评价值视为路程,由于时序相减为单位时间内的变化,故静态评价值的时序相减可视为速度[2],对其综合评价结果进行分析。本文在此基础上还将原规范化数据视为路程,而规范化数据的时序相减视为速度。速度和加速度的大小表示的快慢,正负号表示变化的方向。当速度大于0时,若加速度大于0,则处于加速增长趋势;若加速度小于0,则处于减速增长趋势;若加速度等于0,则处于匀速增长趋势。当速度小于0时,若加速度大于0,则处于加速下降趋势;若加速度小于0 ,则处于减速下降趋势;若加速度等于0,则处于匀速下降趋势。当速度等于0时,需具体分析。单位时间速度表示瞬时速度,可以作为静态综合评价值和特征指标值短期变化的比较,而将瞬时速度加和或者加和的平均值,可以作为静态综合评价值和特征指标值长期变化的比较,以便对各时期静态综合评价结果和最终动态综合评价结果及各时期特征指标的变化进行评价结果分析和原因分析并找到待评方案的优势和不足得到改进点。
4.1 各时期静态综合评价结果分析及步骤
评价结果分析。静态综合评价值的“速度化”公式和“加速度化”公式的运用及相关步骤。

=tK(Ni)-(t-1)K(Ni),t=2,3,…,l
特别的,当t=1时,1V(K(Ni))=0
结合式(1.2),以1为单位时间段,则基于速度的静态综合评价值“时间-物元矩阵”表示为:

=tV(K(Ni))-(t-1)V(K(Ni)),t=3,4,…,l
特别的,当t=1、2时,tA(K(Ni))=0。
结合基于速度的静态综合评价值“时间-物元矩阵”,以1为单位时间段,则基于加速度的静态综合评价值“时间-物元矩阵”表示为:
4.2 产生动态综合评价结果的原因分析
产生动态综合评价结果的原因分析。特征指标值的“速度化”公式和“加速度化”公式的运用及相关步骤。


=tξij-(t-1)ξij,t=2,3,…,l
特别的,当t=1时,1V(Cj(Ni))=0。
结合式(1.3),以1为单位时间段,则基于速度的特征指标值的“时间-变量矩阵”表示为:
(2)特征指标值的变化值的变化矩阵“加速度化”。设加速度用A表示,第Ni个物元其在t时刻第j个特征指标值的“加速度化”值可以表示为tA(Cj(Ni)),令:
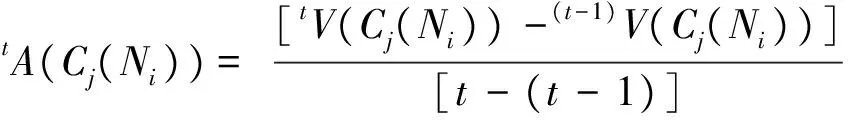
特别的,当t=1、2时,tA(Cj(Ni))=0。
结合基于速度的特征指标值的“时间-变量矩阵”,以1为单位时间段,则基于加速度的特征指标值“时间-特征矩阵”表示为:
同时将各时期特征指标值、速度以及加速度乘以各特征指标相应的权重加和得到的各种评价值即为各时期的静态综合评价值、速度值评价值以及加速度评价值。从而将综合评价结果分析与产生结果的原因分析得到完美的结合。使综合评价结果合理完善,同时还能找到改进点满足多种使用者的需求。
5 算例
本文应用党耀国等[12]中的案例进行分析。
5.1 数据处理
(1)原始数据各时段的规范化决策矩阵也与党耀国等[12]相同。
(2)各时段静态综合评价值、排序及速度特征分析。以下为以平均值为中心的规范化数据利用物元法简易计算的静态综合评价值、排序及速度特征分析值,结果如表2 所示。
(3)静态综合评价值的分类。根据表1物元t时刻的“五线谱”静态分类标准图,以下为各物元不同时间段的静态综合评价值的分类,结果如表3所示。
(4)静态综合评价及其分类的结果分析。表2、表3为以各特征指标平均值为标准计算的静态综合评价值和其变化情况及其分类,可知:静态综合评价各时期排序结果不一致,这为投资银行具体选择哪家企业进行投资产生一定的困扰而无法做出正确的决策,故而有必要考虑不同时期的数据进行动态综合评价。但静态综合评价值也有一定的作用,其为动态综合评价的基础。由于各时期评价值均在先进平均值以下处于第二、三类离理想值还有较大差距,都有较大的提升空间。
(5)动态综合评价、排名及分类。以下为各物元动态综合评价值及其分类,结果如表4和表5所示。
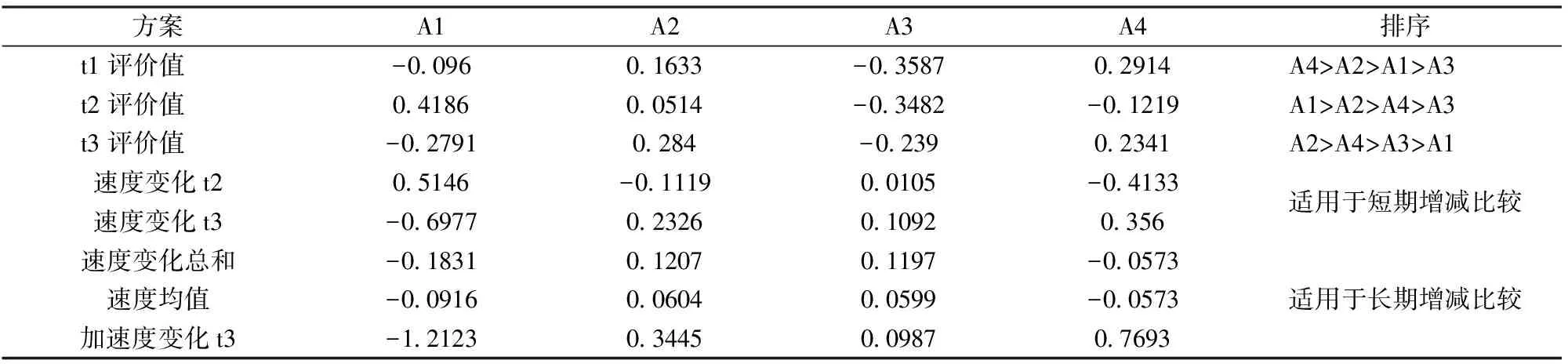
表2 各时段静态综合评价值及排序

表3 各时段静态综合评价值的分类
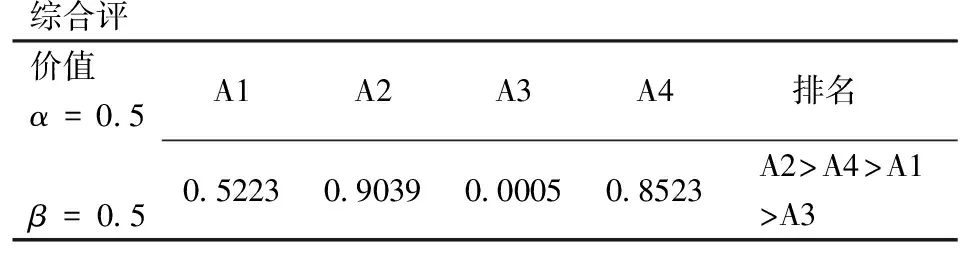
表4 动态综合评价值及其排名
表4、表5为先静态综合评价后经修正静态综合评价计算的理想物元动态综合评价值排名及其分类。取α=0.5,β=0.5由表4可知排序结果A2>A4>A1>A3与文[12]相符。由表5可知A1、A2、A3、A4均处于先进平均值以下与理想值也还有较大差距都具有较大的增长空间。而A2、A4、A1均在平均值以上处于第二类而A3处于落后平均值以下属于第四类差距很大。总之动态综合评价结果与党耀国[12]相符且更加详细全面。
(5)利用特征指标值速度特征分析评价结果产生的原因
5 项决策指标投资净资产率、投资销售率、投资成本率、投资利税率和环境污染程度分别用C1、C2、C3、C4和C5表示。以下为将规范化数据指标利用速度特征分析其指标值变化即速度和指标值变化的变化即加速度,最终找出各物元的优势和劣势并提供改进点,为表6。

表5 动态综合评价值分类结果
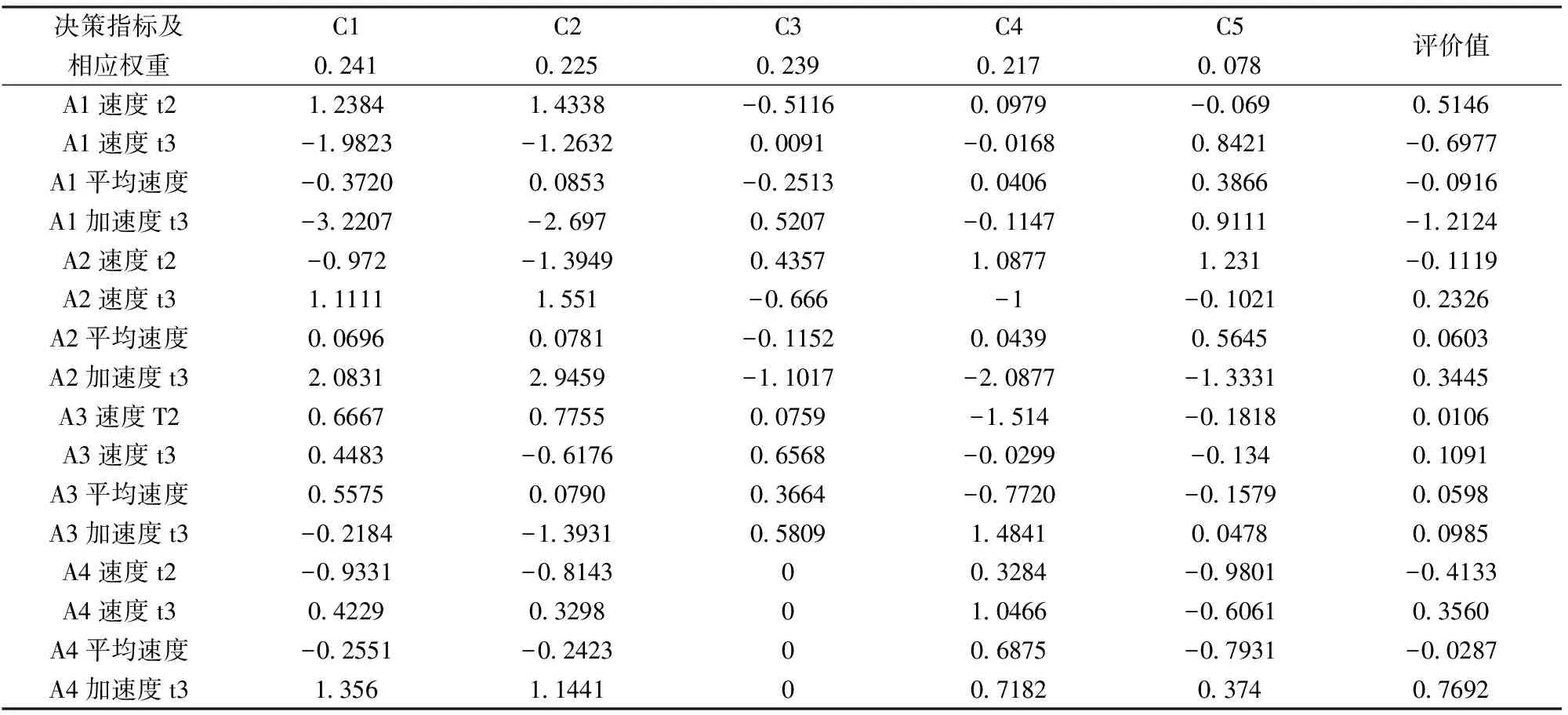
表6 特征指标值的速度特征分析
表6为评价结果产生的原因分析并找出方案的优势及不足并提供改进点。A2表现较好在于指标C1、C2、C4、C5平均速度均为正贡献较大,使其长期综合变化较大,且A2好坏矩阵较好故排在第一位,故动态综合评价排名第一。A3虽长期综合变化为正,但变化不明显而其好坏矩阵基础很差仍靠后所以排在第四位。A1、A4,表现均不显著,分别排在第二、三位。A4中C3速度加速度值均为0,其原因为各年数据同类比较均最大,以此为标准故变化为0。同时从各指标的平均速度来看A1的指标C1、C3为负,A2的指标C3为负,A3的C4、C5为负,A4的C1、C2、C5均为负此为待改进点。
6 结 语
通过物元法利用均值和理想点双标准进行动态综合评价和分类,并引入速度特征分析能够有效改善各评价方案,充分满足了评价者的需求。同时该方法简单可行,结论详细可靠,值得推广,为今后更好的对被评价对象进行的动态综合评价及改进具有很好的实用价值和现实意义。
[1] 王积建. 一种多指标综合评价和决策的新方法 [J]. 统计与决策, 2012, (24): 32-35.
[2] 刘微微, 石春生, 吴际. 具有速度特征的动态评价方法及应用 [J]. 中国软科学, 2010, (10): 180-185.
[3] 郭亚军, 唐海勇, 曲道钢. 基于最小方差的动态综合评价方法及应用 [J]. 系统工程与电子技术, 2010, 32(6): 1226-1229.
[4] 宋捷, 党耀国, 王正新. 基于强“奖优罚劣” 算子的多指标灰靶决策模型 [J]. 系统工程与电子技术, 2010, 32(6): 1229-1232.
[5] 易平涛, 张丹宁, 郭亚军, 等. 动态综合评价中的无量纲化方法 [ J]. 东北大学学报(自然科学版), 2009,30(6): 889-892.
[6] 糜仲春, 黄召明. 基于组合赋权的高速公路上市公司绩效动态综合评价 [J]. 中国管理科学, 2008, (专辑): 235-240.
[7] 郑少锋, 何凤平, 霍学喜. 农业上市公司经营业绩的时序多指标综合评价 [J]. 中南大学学报(社会科学版), 2008, 14(1): 84-88.
[8] 郭亚军, 姚远, 易平涛. 一种动态综合评价方法及应用[J].系统工程理论与实践, 2007, 27(10): 145-149.
[9] 王雪荣. 一种基于证据理论的动态综合效绩评价实用方法 [J]. 中国管理科学, 2006, 14(4): 121-127.
[10] 王璐, 庞皓, 何平. 一种新的动态综合评价模型及应用 [J]. 统计与决策, 2006, (24): 28-30.
[11] 饶从军, 肖新平. 风险型动态混合多属性决策的灰矩阵关联法[J]. 系统工程与电子技术, 2006, 28(9): 1353-1357.
[12] 党耀国, 刘思峰, 刘斌, 等. 基于动态多指标灰色关联决策模型的研究 [J]. 中国工程科学, 2005, 7(2): 69-72.
[13] 金菊良, 汪淑娟, 魏一鸣. 动态多指标决策问题的投影寻踪模型 [J]. 中国管理科学, 2004, 12(1): 64-67.
[14] 王坚强.“奖优罚劣”的动态多指标灰色关联度模型研究 [ J]. 系统工程与电子技术, 2002, 24(3): 39-41.
[15] 王欣荣, 樊治平. 上市公司财务状况的动态多指标综合评价方法 [J]. 系统工程理论与实践, 2002, 22(4): 54-58.
[16] 宋如顺. 基于小波神经网络的多属性决策方法及应用 [J].控制与决策, 2000, 15(6): 765-768.
[17] 陈衍泰, 陈国宏, 李美娟. 综合评价方法分类及研究进展 [J]. 管理科学学报, 2004, 7(2): 69-79.
[18] 王宗军. 综合评价的方法、问题及其研究趋势 [J]. 管理科学学报, 1998, 1(1): 75-79.
[19] 钱巍, 冯玉强, 呼大永. 基于关联函数确定组合拍卖商品的可行组合空间 [C]//第十三届中国管理科学学术的会,浙江,杭州,2011年10月25日-28日;63-68.
[20] 余永权. 可拓检测技术 [J]. 中国工程科学,2001, 3(4): 88-94.
[21] 蔡文. 可拓学概述 [J]. 系统工程理论与实践, 1998, 18(1): 76-84.
[22] 郭媛媛. 张玉红. 基于可拓学与BSC的房地产企业绩效评价研究 [J]. 工程管理学报, 2010, 24(1):113-118.
Dynamic Comprehensive Evaluation and Speed Characteristics Analysis of a Matter-Element Method
LIAO Zhi-gao1, ZHAN Min1, XU Jiu-ping2
(1.School of Management, Guangxi University of Science and Technology, Liuzhou 545006,China;2.Business School of Sichuan University, Chengdu 510064,China)
For dynamic multiple attribute decision making problems, a matter-element method classification dynamic comprehensive evaluation method is put forward, and speed characteristics analysis data improvement measures also are proposed. Firstly, through correlation analysis link qualitative and quantitative factors, let those factors quantitative; Then, after "retiring" standardized data, from two angles of mean and ideal point for reference, and adopt advanced "average" and "backward" average classification and dynamic comprehensive evaluation; And on this basis, the use of speed characteristic analysis the reason and improvement measures are put forward. Finally, through a numerical example shows the feasibility and effectiveness of those methods.
matter-element method; classification; dynamic comprehensive evaluation; speed characteristics analysis.
2014-01-06;
2014-08-01
国家自然科学基金重点资助项目(70831005)
廖志高(1977-),男(汉族), 湖南隆回人,广西科技大学管理学院教授,博士,研究方向:不确定决策理论与方法、物流与供应链管理.
1003-207(2015)11-0119-09
10.16381/j.cnki.issn1003-207x.2015.11.015
C934
A
