采购价格柔性策略与供应链利润风险分析

慕银平, 刘利明

(电子科技大学经济与管理学院，四川 成都 610054)

采购价格柔性策略与供应链利润风险分析

慕银平, 刘利明

(电子科技大学经济与管理学院，四川 成都 610054)

面对原材料市场价格的大幅波动，供应链节点企业需要采用相应策略来规避价格波动带来的风险。本文通过设计价格柔性合同，分析供应链企业通过采购价格柔性策略来缓解采购价格波动给企业利润带来的风险。采用Stackelberg主从博弈模型研究得出了制造商的最优采购数量和供应商的最优价格柔性系数，并分别分析了各最优结果随采购价格柔性合同参数的变化趋势。利用供应链各主体的利润方差度量各自承担的利润风险，分析了供应商和制造商的利润风险随采购价格柔性合同参数的变化规律。

供应链管理；采购价格柔性合同；Stackelberg博弈；风险分担

1 引言

2005年后，主要农产品价格出现了快速、大幅、全面、反季节上涨的异常波动，成为推动CPI上行的重要因素[1]。玉米价格呈现“升-降-升”的走势，由2010年初的1746元/吨上涨至年中1976元/吨后缓慢回落，11月份重拾升势，至年底创出1990元/吨的历史最高点，累计上涨14.0%。晚籼稻价格稳步上行，从2010年初的1918元/吨上涨至年底2277元/吨的历史最高点，涨幅为18.7%。大豆、食用油价格先抑后扬，大豆价格由2010年初的3760元/吨震荡下行，至10月创出年内3500元/吨的新低，之后迅速上扬，至11月底上涨至3982元/吨，涨幅达到13.8%。食用油价格从2010年初开始逐渐下降，至4月达到最低点，之后震荡上行，年底较最低点上涨30.9%。棉花、食糖价格先涨后落，棉花价格由2010年初14879元/吨一路攀升至的31302元/吨，涨幅高达110.4%，之后回落至26248元/吨，回落幅度为16.1%。食糖价格由2010年初5271元/吨缓慢上行，进入10月份后突然发力，由6118元/吨陡升至11月的7518元/吨，一个月内涨幅达到22.9%，累计上涨42.6%，之后回落至年底的7004元/吨，回落幅度为6.8%[2]。主要农产品价格波动的益发剧烈，使以农产品为原材料生产的企业承受了巨大的风险，并且极大地影响了人们的日常生活。因此，设计一个采购价格柔性合同以缓和原材料价格的剧烈波动是亟需的。

许多学者以各种方式拓展批发价合同以实现供应链绩效的提升和风险水平的降低，如考虑转运[3-4], 信息不对称[5], 快速响应[6]等。另一方面，柔性合同的设计也越来越受到学术界的关注，研究表明，期权或类期权合同，如回购合同[7]，数量柔性合同[8]能够使制造商/供应商和零售商共同分担需求风险进而提升供应链效率。根据柔性的类型，通常有三类柔性合同被大量研究和应用，看涨期权合同[9]，看跌期权合同[10-11]和双向期权合同[12]。Zhao Yingxue等[13]运用合作博弈方法研究制造商主导的供应链协调问题，研究发现期权合同能够协调供应链且实现供应链效率的Pareto改进。Chen Xu[14]等证明了期权合同能够协调损失厌恶零售商和风险中性供应商组成的供应链系统。汪贤裕等[15]建立了含有比例回购策略和折价回购策略的模型，研究结果表明返回策略可以协调供应链，供应链协调时风险在供应商和销售商之间的分担情况由回购折价参数和回购比例参数决定,并且风险分担情况符合一般的收益和风险之间的权衡关系。刘珩等[16]在前景理论框架下，探讨了存在缺货损失下的由损失厌恶型零售商和风险中性型供应商组成的供应链价格补贴契约设计。陈长彬等[17]通过一个弹性数量契约分析了供应链上的合作双方在信息共享的条件下与信息非共享的条件下对双方运作绩效的改进，并考虑了在信息显示成本较大的情况下，对供应链中合作的双方进行信息显示成本分担的供应链弹性契约设计。王道平等[18]在需求不确定且与价格具有相关性的情况下，通过建立部分回购策略与增量返利策略相结合的联合契约来实现供应链协作。然而，上述文献均是研究供应链契约对供应链利润及协调的影响，但是这些文献都假设需求不确定而价格确定不变或直接给定价格补贴，而本文的研究重点考虑价格的不确定性给供应链节点企业带来的影响。Li和Kouvelis[19]研究了价格不确定情况下的供应合同，为不同类型的供应合同提出了估值方法。Li和Kouvelis[19]的讨论描述了时间柔性、数量柔性、供应商选择以及风险分担等如何减少在价格不确定情况下的采购成本。但Li和Kouvelis[19]假设市场需求确定不变，而本文主要研究市场需求随机波动下的柔性合同设计及供应链风险度量问题。Bassok和Anupindi[20]分析了在产品需求不确定，买方定期下订单的供应合同，得出在给定最低起订量和折扣价格情况下的最优订购策略。Tsay和Lovejoy[21]提出在供应链中协调物流及信息流的方法——数量柔性合同，该合同规定了每期订货数量的最大变动比例[21]。但这两篇文献只考虑了采购数量的柔性变动，而本文着重考虑现实中企业普遍使用的价格柔性合同。Fotopoulos等[22]研究了价格不确定条件下的柔性供应合同，文中设计了一个在变化的价格环境中的供应合同，研究了在考虑成本和贴现因子的情况下的价格过程特性，Fotopoulos等[20]确定了合同的期望低价格的表达式，并且描述了随着时间地移动最优购买时间是如何变化的[22]。但该研究假设原材料不存在现货市场，而本文分析了更加切合实际的存在原材料现货市场的情形。关于供应链契约的更为详细的研究综述可参见王迎军[23]，该研究将当前研究的供应链契约进行分类，并建立了几种典型供应链契约的基本模型。

本文考虑市场需求及原材料价格不确定情况下，供应商和制造商通过签订采购价格柔性合同缓解原材料价格的剧烈波动给供应链带来的风险，并且探讨了采购价格柔性合同下的供应链风险分担策略。

2 符号定义及合同设计

2.1 符号定义

p：单位原材料的市场价格；

pc：合同价格；

r：单位产品的市场零售价；

θ：产品的市场需求；

cs：供应商的单位生产成本；

w：供应商批发原材料给制造商的执行价格。

2.2 合同设计

采购价格柔性合同是供应商根据自己的利润最大化制定的批发供货合约，该合同有两个需要确定的参数：价格柔性系数λ(0≤λ≤1)及合同价格pc。本文假设价格柔性系数λ和合同价格pc由供应商根据自己利润最优确定，单位原材料市场价格p为随机外生变量，其分布函数和密度函数分别为F(p)、f(p)，均为连续、可微函数，且原材料价格p的均值为μp。产品市场需求θ也是随机外生变量，其分布函数和密度函数分别为G(θ)、g(θ)，均为连续、可微函数。当单位原材料市场价格为p时，制造商从供应商处批发原材料的执行价格为pc+λ(p-pc)，即：

w=pc+λ(p-pc)

当价格柔性系数0<λ<1时，价格柔性合同在供应链节点企业间起着风险分担的作用；当价格柔性系数λ=0时，w=pc(注：当w=pc时，λ可以不为0)，不管原材料市场价格如何变化，供应商均以恒定合同价格pc向制造商批发原材料。当价格柔性系数λ=1时，w=p，即采购价格完全随行就市，当原材料价格上涨时，制造商将承担利润下降的风险，而当原材料价格下跌时，供应商将承担利润下降的风险。

3 模型建立

假设供应链由一个上游供应商和一个下游制造商构成，决策过程为：供应商先作决策，确定最优的价格柔性合同参数，制造商根据供应商提供的价格柔性合同做出订货决策。所以供应链上的供应商和制造商构成一个主从博弈，即Stackelberg博弈，供应商是主，制造商是从。模型的求解方法是：根据Stackelberg博弈的逆向归纳法，先根据制造商的期望利润最大求解制造商的订货量q关于供应商价格柔性系数λ的反应函数，然后将该反应函数代入供应商的期望利润函数，求解使供应商的期望利润最大的价格柔性系数λ*，最后将λ*代回q得到制造商的最优订货量q*。

3.1 制造商的最优采购决策

制造商以恒定单位价格r将产品销售到市场，假设r>p，当制造商的订货量q小于市场需求θ时，其销售收入为rq；当制造商的订货量q大于或等于市场需求θ时，其销售收入为rθ。用πr(q)表示制造商的利润函数，其表达式如下：

根据制造商利润函数的表达式和p、θ的分布函数及密度函数可求得制造商期望利润函数如下：

制造商的期望利润函数两边同时对q求一阶偏导数可得下式：

∂E(πr)/∂q=r-rG(q)-[pc+λ(μp-pc)]

制造商的期望利润函数两边同时对q求二阶偏导数可得下式：

∂2E(πr)/∂q2=-rg(q)<0

因此，根据制造商的期望利润函数E(πr)关于订货量q的二阶偏导数小于0可得以下结论：

结论1 制造商的期望利润函数E(πr)是关于订货量q的严格凹函数。

结论1表明，给定供应商价格柔性系数λ的前提下，存在最优的订货量q。

根据凹函数的性质可知，当∂E(πr)/∂q=0时可解得制造商的最优订货量q满足下式：

r-rG(q)-[pc+λ(μp-pc)]=0

(1)

求解 (1) 式，可得制造商的订货量q关于价格柔性系数λ的反应函数为：

q*=G-1(1-[pc+λ(μp-pc)]/r)

(2)

对q作比较静态分析，可得：

∂q/∂λ=(pc-μp)/[rg(q)]

(3)

∂q/∂r=[1-G(q)]/[rg(q)]>0

(4)

∂q/∂pc=-(1-λ)/[rg(q)]≤0

(5)

根据 (3) 式、(4) 式和 (5) 式作如下分析：

(i)价格柔性系数λ与制造商的订货量q之间的关系取决于原材料市场价格均值μp和合同价格pc的相对大小；

(ii)产品市场零售价格r增大，可以提高制造商的销售收入，进而提高其期望利润E(πr)，从而促使制造商提高订货量q；

(iii)合同价格pc增大，说明制造商从供应商处批发原材料的成本提高，进而制造商的期望利润E(πr)降低，从而促使制造商降低订货量q。

3.2 供应商的最优合同参数确定

根据2.2设计的价格柔性合同可知，供应商以价格w=pc+λ(p-pc)将原材料批发给制造商，用πs(λ,pc)表示供应商利润函数，其表达式如下：

πs(λ,pc)=wq-csq=[pc+λ(p-pc)]q-csq

供应商的利润由销售收入wq及生产成本csq构成。

根据供应商的利润函数和p的分布函数及密度函数容易求得供应商的期望利润函数如下：

E(πs)=[pc+λ(μp-pc)]q-csq

(6)

根据利润最大化的原则，(6) 式两边分别对λ求一阶偏导数如下：

∂E(πs)/∂λ=∂q/∂λ[pc+λ(μp-pc)-cs]+q(μp-pc)

(7)

由 (7) 式两边同时对λ求一阶偏导数，即供应商的期望利润函数对λ求二阶偏导数如下：

∂2E(πs)/∂λ2=-(μp-pc)2/[rg(q)]{g′(q)[pc+λ(μp-pc)-cs]/[rg2(q)]+2}

(8)

本文假设需求函数满足递增失败率(IncreasingFailureRate,IFR)[24]条件，常见的需求分布诸如：均匀分布、指数分布、正态分布、Weibull分布与Gamma分布等都满足递增失败率的条件。根据递增失败率条件，可知：

{g(q)/[1-G(q)]}′>0

(9)

所以，由 (9) 式可得：

g′(q)>-g2(q)/[1-G(q)]

每次我想到这里都会不寒而栗，我害怕那双无形的眼睛某一天会杀我灭口，也害怕终有一天我会因为东窗事发而被公安机关抓获。但我不敢去自首，也不愿去自首，上帝可以作证，我来到世间21年我可是连女孩子的手指头都没有碰过一下啊！我知道自己有罪，如果我当晚就去自首，短裙子女孩、刘伟、黑背心、泰森都是有可能被抓获的，案件就有可能大白于天下的。

令 (8) 式小于零，则需验证：

g′(q)>-[2rg2(q)]/[pc+λ(μp-pc)-cs]

(10)

要使 (10) 式成立，即要满足：

-[2rg2(q)]/[pc+λ(μp-pc)-cs]<-g2(q)/[1-G(q)]

(11)

化简后 (11) 式变成：

pc+λ(μp-pc)+cs>0

根据G(q*)=1-[pc+λ(μp-pc)]/r<1可得：

pc+λ(μp-pc)>0

从而可以得知∂2E(πs)/∂λ2<0。

由供应商期望利润函数关于价格柔性系数λ的二阶偏导数小于0可以得出以下结论：

结论2 当产品市场需求θ分布函数满足IFR时，供应商的期望利润函数E(πs)是关于价格柔性系数λ的严格凹函数。

根据凹函数的性质可知，当∂E(πs)/∂λ=0时可解得供应商所决策的价格柔性系数λ表达式如下：

λ*=[rqg(q)-pc+cs]/(μp-pc)

(12)

根据0≤λ≤1可知，λ表达式的分子部分rqg(q)-pc+cs与分母部分μp-pc的符号同时为正或同时为负。

由 (12) 式两边同时对市场零售价格r求一阶偏导数可得：

∂λ/∂r=qg(q)/(μp-pc)

由 (12) 式两边同时对供应商生产成本cs求一阶偏导数可得：

∂λ/∂cs=1/(μp-pc)

由 (12) 式两边同时对合同价格pc求一阶偏导数可得：

∂λ/∂pc=[rqg(q)-μp+cs]/(μp-pc)2

(13)

将λ*的表达式代入 (2) 式可以得到rqg(q)+cs=r[1-G(q)]，将其代入 (13) 式可得：

∂λ/∂pc={r[1-G(q)]-μp}/(μp-pc)2

(14)

将λ*代入 (6) 式可得：

E(πs)=rq2g(q)

(15)

将 (15) 式两边同时对合同价格pc求一阶偏导数可得：

∂E(πs)/∂pc=-(1-λ)[2q+q2g′(q)/g(q)]

根据IFR性质可知：

g′(q)>-g2(q)/[1-G(q)]

所以：

∂E(πs)/∂pc<-(1-λ){2q-[rq2g(q)]/[pc+λ(μp-pc)]}

令2q-[rq2g(q)]/[pc+λ(μp-pc)]>0，于是可得：

rqg(q)+2cs>0

(16)

显然 (16) 式成立，所以：

∂E(πs)/∂pc<0

(17)

由 (17) 式可得如下结论：

结论3 当产品市场需求θ的分布满足IFR时，供应商的期望利润E(πs)将会随着合同价格pc的增大而减小。

3.3 供应链均衡结果分析

本节从供应链整体的角度分析供应商和制造商的博弈优化结果，确定供应链的采购策略和合同参数的均衡点。

将(2)式获得的制造商订货量关于供应商价格柔性系数λ的反应函数表达式q(λ)代入(12)式供应商的价格柔性系数λ表达式，在给定市场需求的分布函数和概率密度函数G(θ)、g(θ)的条件下，可得出供应链最优的价格柔性系数λ*为：

λ*=[rq(λ*)g(q(λ*))-pc+cs]/(μp-pc)。

将λ*代回(2)式，求解供应链的最优订货量均衡结果。可得最优的订货量q*为：

q*=G-1(1-[pc+λ*(μp-pc)]/r)。

由结论3可以看出，在确保批发执行价格w大于生产成本cs的情况下，供应商会尽可能降低合同价格pc以增加制造商的订货量q，最终使期望利润E(πs)增加。

由于决策时，市场价格p未知，因此只能根据期望进行决策。因此，批发价格的最优表达式为：

w*=pc+λ*(μp-pc)。

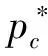
4 供应链各主体利润风险分析

4.1 供应商利润风险分析

针对供应商的利润函数πs求方差可得供应商的利润风险表达式如下：

(18)

(18) 式两边同时对价格柔性系数λ求一阶偏导数可得：

所以，根据供应商利润函数方差对价格柔性系数λ的一阶偏导数表达式可以作如下分析：

供应商和制造商在签订采购价格柔性合同时，一般情况下恒定合同价格pc大于供应商的生产成本cs。当然，在收益共享合同中，合同价格pc也有可能小于供应商的生产成本cs，但本文不考虑收益共享合同的情况，所以pc>cs。

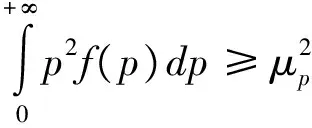
根据以上分析可以得出，如果供应商对风险的态度是厌恶型，其为了降低所承担的利润风险会尽可能降低价格柔性系数λ，最终使λ=0，此时制造商从供应商处批发原材料的执行价格w=pc恒定不变。风险中性或风险偏好的供应商并不会一味降低价格柔性系数λ，而是在风险与收益均衡的时候取最优价格柔性系数λ。

(18) 式两边同时对合同价格pc求一阶偏导数可得：

当r[1-G(q)]<μp时，∂D(πs)/∂pc<0，即供应商所承担的利润风险D(πs)与合同价格pc成反比关系，合同价格pc的增大可以减小供应商所承担的利润风险D(πs)。于是可以得到以下结论：

如果供应商对风险的态度是厌恶型，当r[1-G(q)]<μp时，供应商为了降低其所承担的利润风险会尽可能增大合同价格pc。

4.2 制造商利润风险分析

针对制造商的利润函数πr求方差可得制造商的利润风险表达式如下：

(19)

(19) 式两边同时对价格柔性系数λ求一阶偏导数可得：

(19) 式两边同时对合同价格pc求一阶偏导数可得：

当r[1-G(q)]<μp时，∂D(πr)/∂pc<0，即制造商所承担的利润风险D(πr)与合同价格pc成反比关系，合同价格pc的增大可以减小制造商所承担的利润风险D(πr)。

于是可得，如果制造商对风险的态度是厌恶型，当r[1-G(q)]<μp时，制造商为了降低其所承担的利润风险有增大合同价格pc的要求。

5 数值算例

E(πr)=-q2/20+10q-[pc+λ(6.5-pc)]q两边同时对q求二阶偏导数∂2E(πr)/∂q2=-1/10<0，于是可求得q*=200-10[pc+λ(6.5-pc)]。

最优订货量q*与价格柔性系数λ及合同价格pc的关系如图1所示。

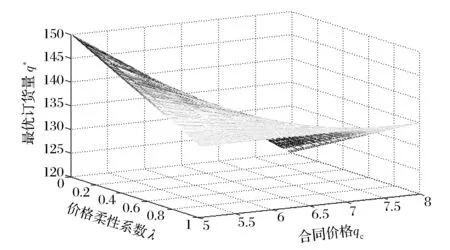
图1 q*与λ、pc二者的关系示意图

图2 E(πr)与λ、pc二者的关系示意图

将q*的表达式代入制造商的期望利润函数E(πr)可得：

E(πr)=5[pc+λ(6.5-pc)]2-100[pc+λ(6.5-pc)]+500

制造商的利润函数E(πr)与价格柔性系数λ及合同价格pc的关系如图2所示。

将q*代入供应商的期望利润E(πs)可得：

E(πs)=-10[pc+λ(6.5-pc)]2+140[pc+λ(6.5-pc)]-400

供应商的利润函数E(πs)与价格柔性系数λ及合同价格pc的关系如图3所示。

图3 E(πs)与λ、pc二者的关系示意图

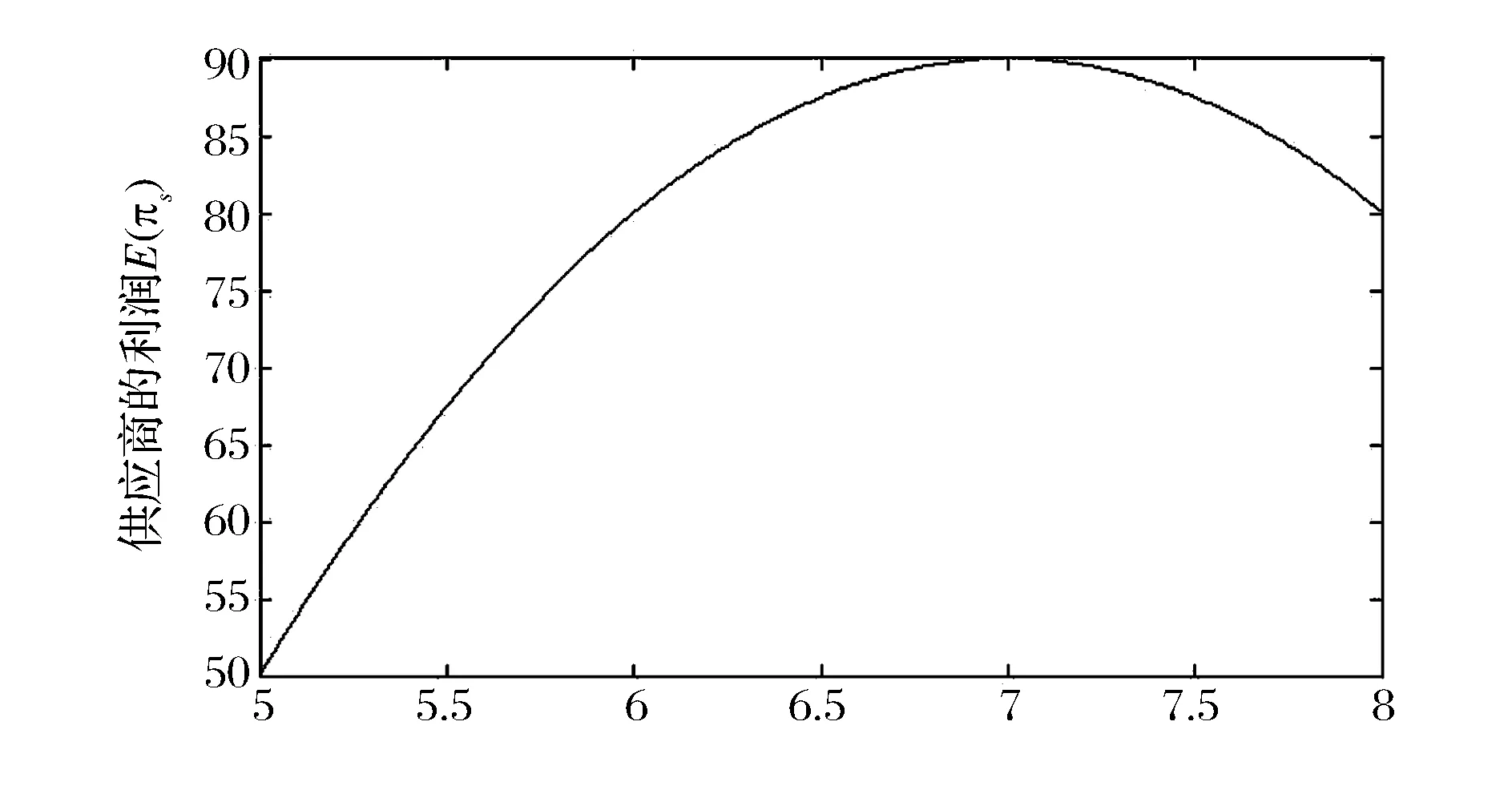
图4 E(πs)与pc的关系示意图

将q*代入供应商的利润风险D(πs)可得：

D*(πs)=7500λ2-1500λ2[pc+λ(6.5-pc)]+75λ2[pc+λ(6.5-pc)]2

供应商的利润风险D(πs)与价格柔性系数λ及合同价格pc的关系如图5所示。

图5 D(πs)与λ、pc二者的关系示意图

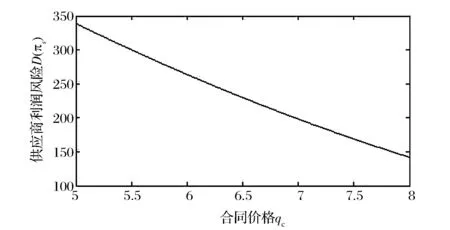
图6 D(πs)与pc的关系示意图

将q*代入制造商的利润风险D(πr)可得：

D(πr)=25[pc+λ(6.5-pc)]4+7500λ2-(4×105+1500λ2)[pc+λ(6.5-pc)]+5000[pc+λ(6.5-pc)]3/3+75λ2[pc+λ(6.5-pc)]2+2.4×106

制造商的利润风险D(πr)与价格柔性系数λ及合同价格pc的关系如图7所示。

当合同价格pc分别取5，6.5，8时，制造商所承担的利润风险D(πr)与价格柔性系数λ的关系如图8所示，pc=5时，由于制造商的利润会随着价格柔性系数的增大而减小，所以制造商所承担的利润风险D(πr)与价格柔性系数λ成反比关系；pc=8时，由于制造商的利润会随着价格柔性系数的增大而增大，所以制造商所承担的利润风险D(πr)与价格柔性系数λ成正比关系。

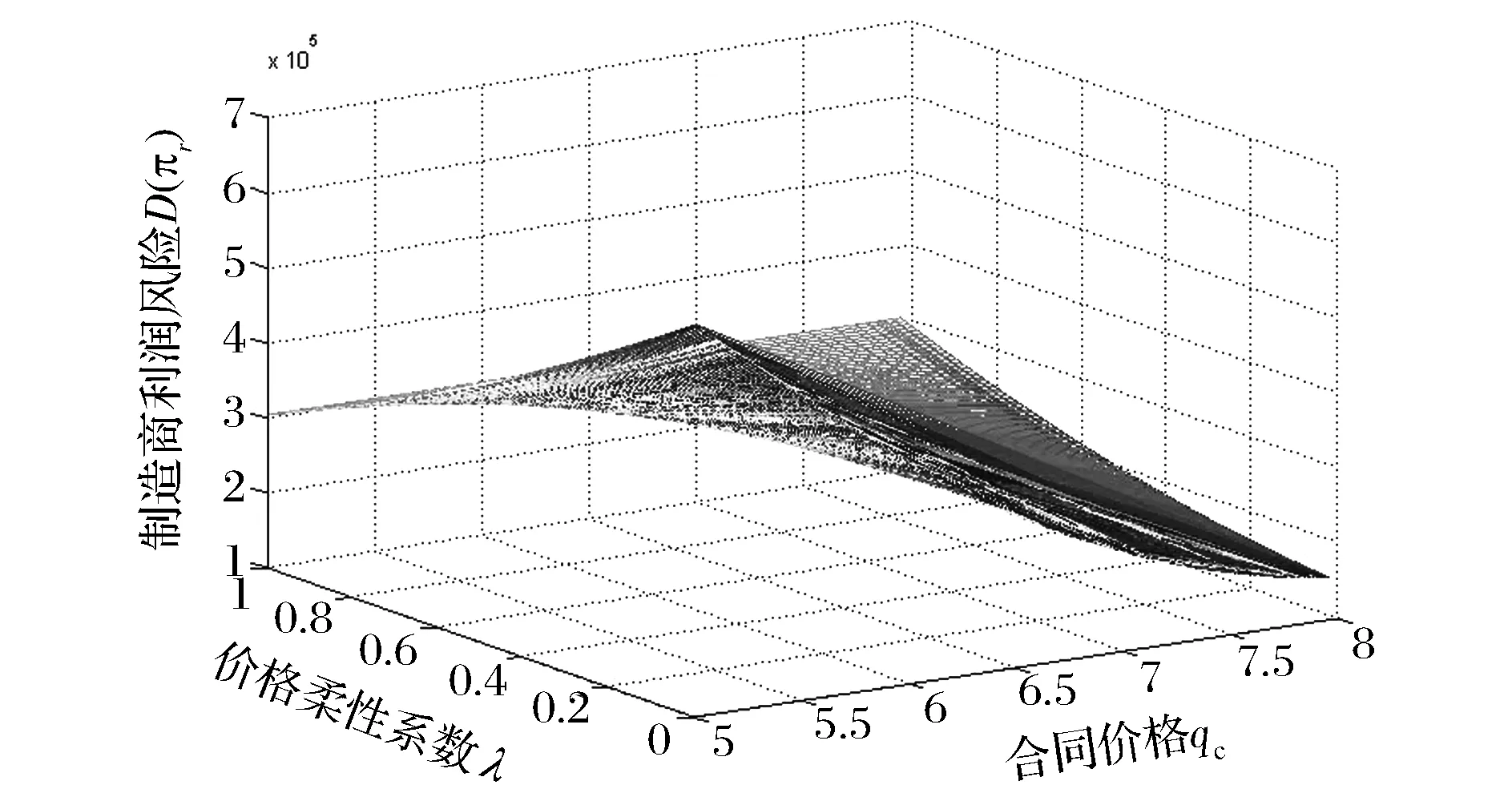
图7 D(πr)与λ、pc二者的关系示意图

图8 D(πr)与λ的关系示意图

6 结语

本文建立了一个供应商和一个制造商的供应链管理模型，研究了供应链企业如何通过设计采购价格柔性合同缓解各供应链主体所承担的利润风险。文中采用利润函数方差刻画利润风险，给出了采购价格柔性合同下的各供应链节点企业所承担的风险情况，并揭示了各供应链节点企业所承担的利润风险随着价格柔性合同参数的变化规律。本文的研究结果将对实践中供应链企业的采购决策提供理论上和方法上的指导。今后进一步的研究可以考虑缺货损失、供应链各主体努力程度及风险偏好等因素对供应链企业最优决策及利润风险大小的影响程度。

[1] 郭峰, 杜晓力. 主要农产品价格走势分析及预测[J]. 农业展望, 2011, 7(1): 49-53.

[2] 黄丽, 罗峰. 国内外农产品价格波动研究及最新进展[J]. 佛山科学技术学院学报, 2011, 29 (1): 39-43.

[4]ShaoJ,KrishnanH,McCormickT.Incentivesfortransshipmentindecentralizedsupplychainswithcompetingretailers[J].ManufacturingandServiceOperationsManagement, 2011, 13(3): 361-372.

[6]KrishnanH,KapuscinkiR,ButzD.Quickresponseandretailereffort[J].ManagementScience, 2010, 56(6): 962-977.

[7]WuDesheng.Coordinationofcompetingsupplychainswithnews-vendorandbuybackcontract[J].InternationalJournalofProductionEconomics, 2013, 144(1): 1-13.

[8]TsayAA.Thequantityflexibilitycontractandsupplier-customerincentives[J].ManagementScience, 1999, 45(10): 1339-1358.

[9]ChenF,ParlarM.Valueofaputoptiontotherisk-aversenewsvendor[J].IIETransactions, 2007, 39(5): 481-500.

[10]WangQunzhi,ChuBongsung,WangJian,etal.Riskanalysisofsupplycontractwithcalloptionsforbuyers[J].InternationalJournalofProductionEconomics, 2012, 139(1): 97-105.

[11]NosoohiI,MollaverdiN.Modelingofcapacityreservationandsupplierselectionbasedonoptioncontract[J].InternationalJournalofIndustrialEngineering&ProductionResearch, 2011, 22(2): 135-141.

[12]ZhaoYingxue,MaLijun,XieGang,etal.Coordinationofsupplychainswithbidirectionaloptioncontracts[J].EuropeanJournalofOperationalResearch, 2013, 229(2): 375-381.

[13]ZhaoYingxue,WangShouyang,ChengTCE,etal.Coordinationofsupplychainsbyoptioncontracts:Acooperativegametheoryapproach[J].EuropeanJournalofOperationalResearch, 2010, 207(2): 668-675.

[14]ChenXu,HaoGang,LiLing.Channelcoordinationwithaloss-averseretailerandoptioncontracts[J].InternationalJournalofProductionEconomics, 2014, 150: 52-57.

[15] 汪贤裕, 肖玉明. 基于返回策略与风险分担的供应链协调分析[J]. 管理科学学报, 2009, 12 (3): 65-70.

[16] 刘珩, 潘景铭, 唐小我. 基于损失厌恶型零售商的易逝品供应链价格补贴契约研究[J]. 控制与决策, 2010, 25 (8): 1149-1154.

[17] 陈长彬, 缪立新. 供应链弹性契约下的信息共享激励[J]. 软科学, 2010, 24 (1): 46-51.

[18] 王道平, 苏红霞, 欧阳强国. 需求价格相关的供应链的联合契约研究[J]. 管理学报, 2009, 6 (4): 440-443.

[19]LiCL,KouvelisP.Flexibleandrisk-sharingsupplycontractsunderpriceuncertainty[J].ManagementScience, 1999, 45 (10): 1378-1397.

[20]BassokY,AnupindiR.Analysisofsupplycontractswithtotalminimumcommitment[J].IIETransactions, 1997, 29(5): 373-381.

[21]TsayAA,LovejoyWS.Quantityflexibilitycontractsandsupplychainperformance[J].Manufacturing&ServiceOperationsManagement, 1999, 1(2): 89-111.

[22]FotopoulosSB,HuXiangling,MunsonCL.Flexiblesupplycontractsunderpriceuncertainty[J].EuropeanJournalofOperationalResearch, 2008, 191 (1): 253-263.

[23] 王迎军. 顾客需求驱动的供应链契约问题综述[J]. 管理科学学报, 2005, 8 (2) : 68-76.

[24]BarlowRE,ProschanF.Statisticaltheoryofreliabilityandlifetesting:Probabilitymodels[M].NewYork:Holt,Rinehart,andWinston, 1975.

FlexibleProcurementPricePolicyandProfit-RiskAnalysisinSupplyChain

MU Yin-ping, LIU Li-ming

(School of Management and Economics, University of Electronic Science and Technology of China, Chengdu 610054, China)

Due to the price fluctuation of the raw materials, supply chain firms need to relieve the risks of the profit decrease through the procurement price flexibility mechanism. In this paper, a supply chain consist of a supplier and a manufacturer is considered, where the manufacturer buys the raw material from the supplier at the beginning of the lead time and the supplier delivers the raw material to the manufacturer at some time later. By designing a procurement price flexibility contract, the risk relief of the contract on the supplier and the manufacture’s profit is analyzed. Using the Stackelberg game, mathematic models are developed to analyze the optimal procurement quantity of the manufacturer and the optimal contract parameters of the supplier. Also the optimal results change trend with the change of the price flexibility contract parameters is discussed. Using variance of the profit the risk undertaken by the supplier and the manufacturer respectively is and measured the change of the risk with the change of the price flexibility parameters is analyzed. The results show that supply contract with proper parameters can improve the profit and relief the profit risk of the supplier and the manufacturer respectively.

supply chain management; procurement price flexibility contract; stackelberg game; risk-sharing

2013-09-26；

2014-08-29

国家自然科学基金资助项目(71172096)；国家自然科学基金重点资助项目(71432003)

慕银平(1976-)，男(汉族)，甘肃镇原人，电子科技大学经济与管理学院博士，教授. 研究方向: 运营管理、供应链管理.

1003-207(2015)11-0080-08

10.16381/j.cnki.issn1003-207x.2015.11.010

F274

A