网上拍卖销售与逆向拍卖采购下的库存管理

刘树人，唐 沛， 黄颖娜

(1. 湘潭大学商学院，湖南 湘潭 411105；2. 湘潭大学数学与计算科学学院，湖南 湘潭 411105)

网上拍卖销售与逆向拍卖采购下的库存管理

刘树人1，唐 沛2， 黄颖娜2

(1. 湘潭大学商学院，湖南 湘潭 411105；2. 湘潭大学数学与计算科学学院，湖南 湘潭 411105)

以电子商务为背景研究网上拍卖销售与逆向拍卖采购下的库存管理。在该问题中，零售商一方面利用网上拍卖销售产品，另一方面利用逆向拍卖进行采购。对于单阶段情形，证明网上拍卖下零售商的期望收益函数是采购量的严格递增的凹函数，从而得到零售商的最优采购策略和供应商的最优投标策略。对于多阶段情形，利用马尔可夫决策过程理论建立该问题的最优控制模型，得到零售商的最优采购策略和供应商的贝叶斯-纳什均衡投标策略均与基本库存策略相类似。

库存管理；网上拍卖；逆向拍卖；马尔可夫决策过程

1 引言

随着互联网和信息技术的发展，电子商务得到了飞速发展和广泛应用，而网上拍卖是电子商务中最成功的一种形式。网上拍卖是拍卖的一种特殊类型，即利用互联网举办拍卖，在网上公开准备出售商品或服务的一些信息，通过竞争投标的方式将它出售给出价最高的投标者。其实质是以竞争价格为核心，建立买者和卖者之间的交流与互动机制，由买卖双方共同确定商品或服务的成交价格与数量，从而达到均衡的一种市场经济过程。网上拍卖为买卖双方提供了具有较低交易成本的平台，强大的列名功能和搜索技术为特定类别的拍卖品产生了巨大的流动市场。根据网上拍卖的特性，例如，顾客群广、交易成本低等，许多大中型商家，比如戴尔、沃尔玛山姆会员店等，都增添了网上拍卖这种新型销售方式。另一方面，在采购方法上，逆向拍卖技术是一种革命性的创新。网上逆向拍卖是发生在采购商和一群事先通过资格审查的供应商之间的在线实时动态拍卖。采购商对商品或服务的设计、数量、质量、配送和相关条款进行定义，供应商运用特定软件在预先设定的时间区间内通过互联网在线投标，异地同时反复竞价，以期最终获得采购合同。网上逆向拍卖由于能有效降低采购价格，为企业采购带来相当可观的成本节约，从而逐步引起实业界和学术界的广泛关注。正如Tunay和Wu Qiong[1]所指出的，现在许多大中型企业都利用网上逆向拍卖来采购所需的原材料或服务。2007年，Sun公司通过逆向拍卖确定的采购合同价值高达27亿美元，占到其当年采购预算的百分之七十。沃尔玛山姆会员店、戴尔、通用电气等正在扩大利用网上逆向拍卖进行采购。基于沃尔玛山姆会员店和戴尔的商业模式，即它们一方面利用网上拍卖销售产品，另一方面利用逆向拍卖进行采购，本文研究联合网上拍卖销售与逆向拍卖采购下的库存管理问题。

与本文库存管理问题相关的工作涉及两个方面。一是利用拍卖机制销售下的库存管理。van Ryzin 和Vulcano[2]是第一篇考虑库存与拍卖联合决策的论文。该文利用马尔可夫决策过程研究了无限阶段折扣准则和平均准则下的最优拍卖与订购，得到基本库存保留价格拍卖策略(Base-stock Reserve-price-auction Policy, BSRA)，并提出了修正的一级或二级价格拍卖机制。进一步地， 在van Ryzin和Vulcano[2]的基础上，Huh 和Janakiraman[3]考虑了订购时有固定订购费用的情形, 利用Huh和Yanakiraman[4]提出的统一性条件证明了当销售通过拍卖实现时商家的最优订购策略是(s,S)策略。LiuShuren等[5]也研究了一类网上拍卖下有固定订购费用的库存控制问题，在一定的条件下得到商家的最优订购策略是(s,S)策略。另一类相关文献研究的是逆向拍卖采购下的库存管理。ChenFangruo[6]研究了一个零售商在有多个潜在供应商条件下的采购问题，这些供应商关于她们的生产成本具有私有信息。为了实现最优采购，零售商的决策是首先确定一个采购合同，然后供应商投标，在数量拍卖(QuantityAuction)中供应商投标数量，而在供货合同拍卖(SupplyContractAuction)中供应商投标一次性的费用，最后通过拍卖方式实现价格发现(成交价)，确定生产成本最低的供应商为获胜者，并由该供应商确定最优的采购量并传递给零售商。进一步地，该文指出供货合同拍卖能很好地解释当前零售业中流行的进场费(SlottingAllowance)和供应商管理库存(Vendor-managedInventory)两种现象。LiCuihong和Scheller-Wolf[7]研究了风险分配下仅基于价格的推式或拉式合同(PushorPullContract)拍卖。Gallien和Wein[8]研究了供应商有容量约束下买者的采购拍卖问题。Chaturvedi和Martinez-de-Albeniz[9]研究了存在供应风险情形下的最优采购拍卖。姚升保[10]研究了基于幂效用函数的多属性采购拍卖。

因此，本文在ChenFangruo[6]的基础上进一步研究联合网上拍卖销售与逆向拍卖采购下的库存管理问题。在该问题中，零售商一方面利用网上拍卖销售产品，另一方面利用逆向拍卖进行采购。对于单阶段情形，证明网上拍卖下零售商的期望收益函数是采购量的严格递增的凹函数，从而得到其最优的采购策略。对于多阶段情形，利用马尔可夫决策过程理论建立该问题的最优控制模型，得到零售商的最优采购策略和供应商的贝叶斯-纳什均衡投标策略均与基本库存策略相类似。

2 单阶段网上拍卖销售与逆向拍卖采购下的库存管理

首先介绍沃尔玛山姆会员店的网上拍卖销售与逆向拍卖采购的运作流程(Auctions.samsclub.com)。在网上逆向拍卖采购方面，沃尔玛山姆会员店首先对供应商的资格进行预审，然后发布竞标书(采购合同)，事先约定竞价条件；经过资格预审合格的供应商，按照规定的时间被安排登录到逆向拍卖平台开始与对手竞争，可以在规定的竞价过程中充分地进行竞争性报价；竞价时间截止时，通常报价最低者获得采购合同。在网上拍卖销售方面，顾客首先在沃尔玛山姆会员店网站注册一个帐户；网站设置顾客的账户的具体信息,包括山姆俱乐部会员号码。然后顾客登录到其帐户，投标自己想购买的物品。顾客通过点击“出价”按钮提交自己的出价，可以在规定的竞价过程中充分地进行竞争性出价。拍卖结束时，网站根据拍卖机制确定物品的分配和支付规则。

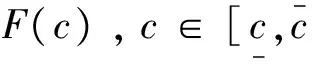
假设零售商的采购量为Q，其相应的期望收益函数为r(Q)(不包括采购费用)。由ChenFangruo[6]可知，如果能够证明r(Q)是严格递增的凹函数，那么ChenFangruo[6]中的最优拍卖机制对这里的单阶段联合网上拍卖销售与逆向拍卖采购下的库存管理问题也成立。因此，下面将证明当需求通过网上拍卖实现时零售商的期望收益函数r(Q)为严格递增的凹函数。

2.1 单阶段网上拍卖销售下的收益函数及其性质

近年来，随着互联网和信息技术的发展，许多大中型商家也都增添了网上拍卖这种新型销售方式；由于产品不具有唯一性，商家采用的拍卖方式大都属于同质多物品拍卖。众所周知，对于同质多物品拍卖有两种主要的机制：歧视性拍卖(Discriminatory Auction，DA)与同一价格拍卖(Uniform Price Auction，UPA)。在每个竞买者最多只能购买一个单位(即单位需求)的情形下，DA 拍卖和UPA 拍卖可被视为一级价格密封拍卖与二级价格密封拍卖在多物品拍卖中的推广。 由同质多物品拍卖的收益等价定理，在DA 拍卖和UPA 拍卖两种机制下商家将得到相同的期望收益。因此，本文主要考虑多单位同一价格拍卖，注意到在同一价格拍卖下顾客以自己对商品的真实估值作为报价。下面考虑商家进行一阶段的同质多物品网上拍卖。

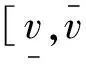
在拍卖开始时商家提供多单位的同质产品，同时他还会为拍卖品制定一个保留价v以防止顾客报低价、抵御投标者之间的合谋行为并保护自己的最低收益。因此当所有顾客的报价均低于这个保留价时, 商家不予出售物品。由前所述，对于该多物品拍卖有歧视性拍卖和同一价格拍卖两种主要的机制。在歧视性拍卖下，若商家提供拍卖的产品是s，而每一位顾客最多只能买一件商品，那么报价最高且超过保留价的前s位获得商品, 并以自己的报价支付；而在同一价格拍卖下报价最高且超过保留价的前s位获得商品，但支付价格为保留价v和第s+1位报价两者中的最大者。这里如果没有第s+1位报价者，则令第s+1位的报价为零。

假定顾客到达数N的概率函数为g(n)。首先计算“一阶段拍卖到达的顾客数中恰好有m个投标者的报价大于等于商家的保留价v”这一事件发生的概率qm，易知:

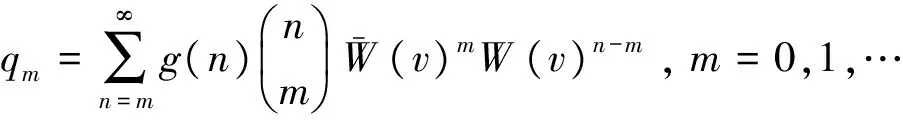
(1)

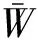
(2)

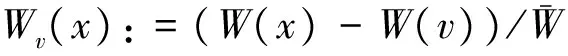
假定在一次拍卖中有m>s个投标者参与拍卖，在同一价格拍卖下这m个投标者以自己对商品的真实估值进行报价，分别记为v1,v2,…,vm， 故报价相互独立且服从概率密度wv(.)，其逆序统计量分别记为v(1)≥v(2)≥…≥v(m)。根据同一价格拍卖规则，具有私有值为v(1)≥v(2)≥…≥v(s)的顾客拍得s件产品，她们的支付均为第一个失去标的拍卖者的报价，即逆序统计量v(s+1)。因此，期望支付价格为:

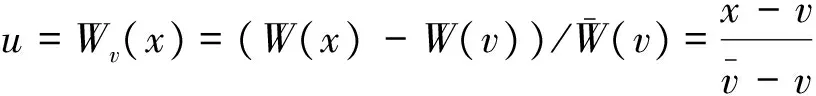
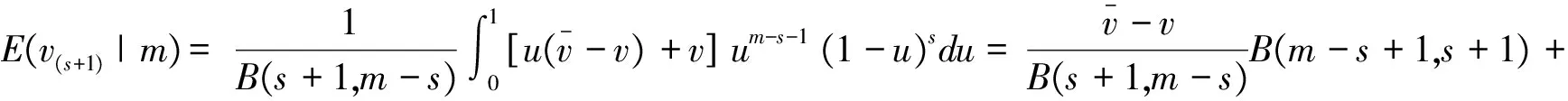
(3)

其中r(0)=0。

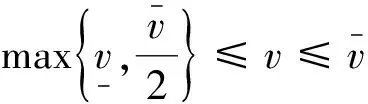
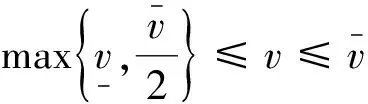
证明见附录A。

2.2 单阶段网上拍卖销售与逆向拍卖采购下的库存管理

由定理1可知，如果零售商的采购量为Q并且全部提供到网上拍卖，那么其相应的期望收益函数为r(Q)(不包括采购费用) 是Q的严格递增的凹函数。故由文[6]可知此时零售商的期望利润函数为:

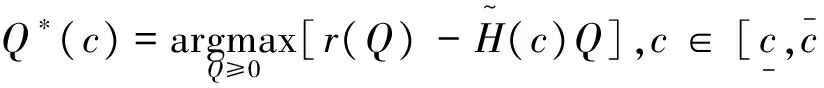
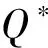
3 多阶段网上拍卖销售与逆向拍卖采购下的库存管理

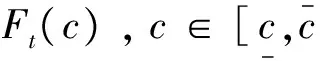
在数量拍卖机制下，每阶段中的运作模式为：期初，零售商观察到库存水平并决定是否采购，若采购，则确定一个采购合同，然后各供应商投标愿意供应/生产的数量，通过拍卖方式实现价格发现(成交价)，即确定投标数量最多(从而也是边际生产成本最低)的供应商为获胜者，由该供应商确定采购量并传递给零售商(该量亦可看作由零售商和获胜的供应商共同确定)。具体地，对于第t阶段，事件发生的顺序如下：

1)零售商观察到第t阶段初的库存水平为i。

2)零售商组织一次数量拍卖(逆向拍卖)。在该机制下，零售商首先确定一个采购合同Pt(Q)并向供应商宣布，该合同表示如果零售商的采购量为Q，那么他支付给供应商的货款为Pt(Q)；然后lt个供应商投标她们各自的供应/生产量，这是一个不完全信息静态博弈，由于每个供应商关于她们的边际生产成本事前对称，故存在一个对称的贝叶斯-纳什均衡投标策略，由此决定采购量Qt。假定采购的滞后期为t0，即在本阶段初采购的产品将在阶段末到货，因而可用于本阶段拍卖。

3)随机需求通过网上拍卖的方式实现，拍卖获胜者在拍卖结束时获得产品。当零售商提供给拍卖的产品为Q+i时，由2.1节可知该阶段的收益函数为r(Q+i)。

4)本阶段末剩余的库存将用于下一阶段拍卖。同时，在本阶段中由于初始库存水平为i零售商需支付存贮费hi。

令Vt(i)表示在联合网上拍卖销售与逆向拍卖采购下的库存控制问题中，第t阶段初的库存水平为i时零售商选择最优策略从第t阶段直到决策阶段末所能获得的最大期望折扣总利润。于是，由马尔可夫决策过程理论可知，Vt(i)满足如下最优方程

(4)

其中(Q)+=max{Q,0},β∈(0,1)表示折扣因子。边界条件VT+1(i)=0表示决策阶段末剩余的产品没有残值，这只是为了简便起见，事实上，只要VT+1(i)是凹函数本节所有的结论仍成立。注意到，由于供应商在进行博弈之前采购量是随机的，所以在(4)中要先求“max”,再关于Ct,(1)取数学期望，这也增加了模型的求解难度。

关于零售商和供应商的最优策略，有如下的重要结论。

定理2 对于联合网上拍卖销售与逆向拍卖采购下的库存控制问题,对t=T,T-1,…,1,

1)Vt(.)为凹函数。

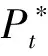
(5)

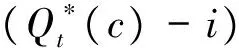
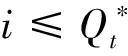
证明见附录B。

注意到，在经典的库存控制模型中，零售商的采购单价和销售单价是外生给定的，他只需确定采购量以最大化其期望利润。因而，在库存控制模型中每阶段只有一个决策者，即零售商。而在多阶段网上拍卖销售与逆向拍卖采购下的库存管理中每阶段零售商、供应商和顾客都是决策者。由于零售商、供应商和顾客之间的信息不对称，零售商的采购单价和销售单价都是随机变量。

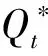
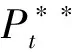
(6)

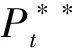
4 结语

本文将库存模型与拍卖理论相结合，研究了单阶段和多阶段联合网上拍卖销售与逆向拍卖采购下的库存管理问题，从理论上刻划了拍卖机制对零售商的最优采购策略的影响，为实际管理者在利用网上拍卖进行销售和逆向拍卖进行采购时提供了参考依据，具有较强的现实意义和应用价值。

联合网上拍卖销售与逆向拍卖采购下的库存管理是一个崭新的课题。虽然本文在有限阶段下得到了很好的结果，进一步需要研究的问题还有很多。例如，关于无限阶段的分析内容更复杂但结果应是类似的，我们将在另文讨论。另外，零售商利用逆向拍卖进行采购的同时也可对供应商进行管理，因此考虑供应商管理下的逆向拍卖将是值得进一步研究的领域，等等。

附录A

定理1的证明: 为证明r(s)是s的严格增函数，只需证明Δr(s)>0。事实上，由(3)式，得:

(*)

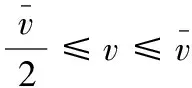
为证明r(s)是s的严格凹函数，只需证明Δ2r(s)<0。事实上，

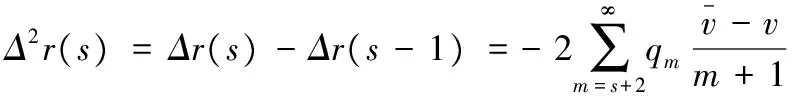
附录B

定理2的证明: 数学归纳法。当t=T时，由于VT+1(i)=0，故(4)式为:

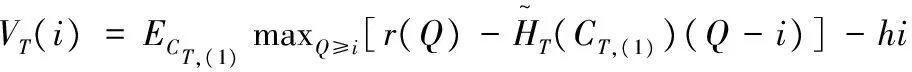
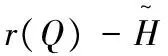
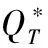
假设定理对t+1时成立。令:

于是，

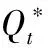
[1]TunayIT,WuQiong.Multiplesourcingandprocurementprocessselectionwithbiddingevents[J].ManagementScience, 2009, 55(5): 763-780.

[2]vanRyzinG,VulcanoG.Optimalauctioningandorderinginaninfinitehorizoninventory-pricingsystem[J].OperationsResearch, 2004, 52(3): 346-367.

[3]HuhWT,JanakiramanG.Inventorymanagementwithauctionsandothersaleschannels:Optimalityof(s,S)policies[J].ManagementScience, 2008, 54(1): 139-150.

[4]HuhWT,JanakiramanG. (s,S)Optimalityinjointinventory-pricingcontrol:Analternativeapproach[J].OperationsResearch, 2008, 56(3): 783-790.

[5]LiuShuren,HuQiying,XuYifan.OptimalinventorycontrolwithfixedorderingcostforsellingbyInternetauctions[J].JournalofIndustrialandManagementOptimization, 2012, 8(1):19-40.

[6]ChenFangruo.Auctioningsupplycontracts[J].ManagementScience, 2007, 53(10): 1562-1576.

[7]LiCuihong,Scheller-WolfA.Pushorpull?Auctioningsupplycontracts[J].ProductionandOperationsManagement, 2011, 20(2): 198-213.

[8]GallienJ,WeinLM.Asmartmarketforindustrialprocurementwithcapacityconstraints[J].ManagementScience, 2005, 51(1): 76-91.

[9]ChaturvediA,Martinez-de-AlbenizV.Optimalprocurementdesigninthepresenceofsupplyrisk[J].ManufaturingandServiceOperationsManagement, 2011, 13(2): 227-243.

[10] 姚升保. 基于幂效用函数的多属性英式拍卖研究[J]. 中国管理科学，2013，21(6)：132-138.

[11]PinkerEJ,SeidmannA,VakratY.Usingbiddataforthemanagementofsequential,multi-unit,onlineauctionswithuniformlydistributedbiddervaluations[J].EuropeanJournalofOperationalResearch, 2010，202(2): 574-583.

[12]DavidHA.Orderstatistics[M]. 2nded.NewYork:JohnWileyandSons, 1981.

[13]PorteusEL.Foundationsofstochasticinventorytheory[M].California:Stanford,StanfordUniversityPress, 2002.

InventoryManagementwithSellingbyInternetAuctionsandPurchasingbyReverseAuctions

LIU Shu-ren1，TANG Pei2， HUANG Ying-na2

(1. Business School，Xiangtan University, Xiangtan 411105,China；2.School of Mathematics and Computational Science，Xiangtan University, Xiangtan 411105,China)

In this paper, an inventory management with selling by Internet auctions and purchasing by reverse auctions is studied in the context of e-commerce. The considered inventory management has the following two characteristics. One is that the retailer sells products by Internet auctions, another one is that the retailer makes procurement management by reverse auctions. For the single-period case, it is shown that the retailer’s expected revenue is a strictly increasing and concave function of the purchased quantity under Internet auctions, leading to the retailer’s optimal procurement strategy and the suppliers’ optimal bidding strategy. For the multi-period case, the optimal control model is first constructed for the retailer by using Markov decision processes. Then, the retailer’s optimal procurement strategy is obtained and the suppliers’ Bayesian-Nash equilibrium bidding strategies are similar to the base-stock policy. These results not only show the effect of auction mechanism on optimal procurement strategy for the retailer, but also provide an important reference for managers to manage inventory under selling by Internet auctions and purchasing by reverse auctions.

inventory management； Internet auction； reverse auction; Markov decision processes

2013-08-15；

2014-09-23

国家自然科学基金资助项目(71401150)

刘树人(1972—)，男(汉族)，湘潭大学商学院博士，副教授，研究方向：运营与供应链管理、拍卖理论.

1003-207(2015)11-0062-08

10.16381/j.cnki.issn1003-207x.2015.11.008

O227;F224

A