多塔斜拉-悬吊协作体桥力学性能探讨

周云岗，杨靖华(1.同济大学建筑设计研究院(集团)有限公司，上海0009; .解放军73049部队，江苏苏州15008)

多塔斜拉-悬吊协作体桥力学性能探讨

周云岗1，*，杨靖华2
(1.同济大学建筑设计研究院(集团)有限公司，上海200092; 2.解放军73049部队，江苏苏州215008)

摘要:采用有限元方法，应用分析软件ANSYS，建立3至6塔主跨跨径为1 400 m的多塔斜拉-悬吊协作桥(简称多塔协作桥)有限元计算模型，研究了索塔数对多塔协作桥静力特性、动力特性和静力稳定性的影响特点，探讨了其对多塔协作桥活载挠度、塔顶纵向位移及主缆抗滑移性能等关键力学问题的影响特征。分析结果表明:索塔数由3塔增至6塔时，塔根弯矩最大增大50%，主梁弯矩最大增大33%，主缆抗滑移系数最大减小36%，中间塔顶位移减小2%，一阶弹性稳定系数最大下降8.3%，颤振稳定性指数最大增加9.2%;主梁边跨竖向挠度比中间跨小36%左右，且中间跨挠度相近;索塔数对索塔受力影响显著。

关键词:多塔斜拉-悬吊协作体系;索塔数;连跨数;静力特性;静力稳定性;动力特性

0　引言

悬索桥和斜拉桥在特大跨桥梁领域具有技术优势，但在力学性能、施工技术以及抗风稳定性等方面遇到了瓶颈。斜拉-悬吊协作体系桥梁(以下简称协作桥)是在两者基础上发展起来的一种组合型式桥梁，克服了诸多不足，具有较好的纵、横向刚度，在技术上优势明显［1］。21世纪，跨江跨海大桥成为桥梁建设主题，多塔缆索承重桥应运而生，成为未来桥梁发展的一个重要方向［2］。

当前，斜拉-悬吊协作体系桥梁主要停留在方案设计阶段［3］，相关理论研究较少。文献［4］研究了斜拉-悬吊协作体系桥温度荷载作用下的静力行为;文献［5-6］分析研究自锚式斜拉-悬吊协作体系的静动力特性、施工步骤、经济性能、运营阶段悬吊部分端吊索的疲劳问题和施工阶段结构的抗风稳定性;文献［7］对比分析了自锚式和地锚式斜拉-悬吊协作桥在温度作用下的异同点;文献［8］从抗风性能角度探讨了斜拉-悬吊协作体系桥的合理结构型式;文献［9］探讨了一致输入、行波输入下斜拉-悬吊协作桥的地震响应，研究了粘滞性阻尼器参数变化对结构减震的影响;文献［10］研究了3塔斜拉-悬吊协作体系桥的位移特征。已有研究成果大多集中在传统双塔桥梁，3塔及以上相关研究成果相对匮乏。

笔者基于ANSYS平台，建立3至6塔斜拉-悬吊协作桥有限元分析模型，通过对比分析，研究了索塔数对其静力性能、动力性能和静力稳定性的影响特点，并进一步探讨其关键力学性能。

1　研究对象

根据传统大跨径斜拉-悬吊协作体系的科研成果，拟定3～6塔协作桥的总体布置方案如图1所示，其中，4～6塔协作桥悬吊和斜拉部分的布置方式与3塔相同。另外，考虑到结构对称性，图中仅示出左半桥。

主梁和索塔典型断面如图2，截面几何特性如表1。主梁采用流线型扁平钢箱梁，塔根处主梁的轴力较大，主梁板厚适当加厚。边塔采用全混凝土结构，中塔采用全钢结构。索塔截面形式为单室箱型，纵、横桥向宽度均由塔顶至塔底线性增加。

图2　塔、梁典型断面图Fig.2　Typical section of tower and beam

表1　典型截面几何特性Tab.1　Geometrical properties of typical section

采用单主梁模式建立ANSYS分析模型，3塔协作桥计算模型如图3所示。主梁和索塔采用空间梁单元(Beam44)模拟，拉索与主梁之间通过刚性杆相连，斜拉索采用只受拉杆多段杆单元(link10)模拟。塔、梁之间耦合横向自由度，墩、梁之间耦合竖、横向自由度。

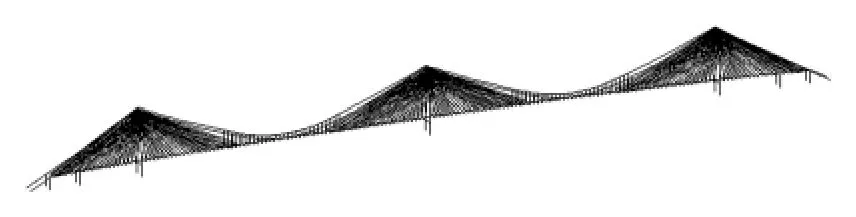
图3　三塔协作桥计算模型Fig.3　Analysis model of three-tower cable-stayed suspension bridge

结构荷载设计值参照苏通长江大桥、泰州长江大桥和舟山连岛工程等桥梁的设计条件确定:一期恒载按材料密度确定，二期恒载按70 kN/m考虑。

2　静力特性

2.1典型工况特点

缆索承重桥属柔性结构，且跨径越大越显著。计算结果表明:恒载、活载、均匀升降温以及极限静阵风等工况的作用效应占主导地位，能较全面地体现缆索承重桥梁的力学特性。为利于表述，图4给出主梁主跨和索塔编号。

采用完全几何非线性静力分析理论，确定各方案的合理成桥状态。恒载作用下，结构处于平衡状态，索塔纵向变形很小，塔根弯矩如图5所示，对应的弯曲应力约为0.03 MPa，基本可忽略不计。可见，结构受力和变形与索塔数无关。

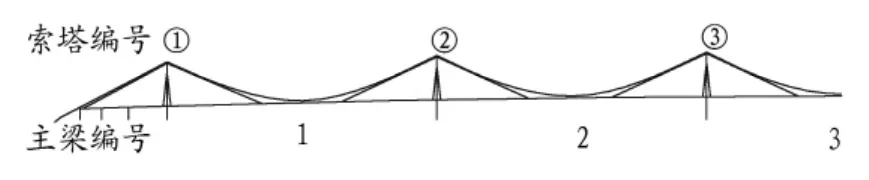
图4　主梁及索塔编号Fig.4　Serial number of tower and span

图5　恒载作用下塔根弯矩Fig.5　Bending moment diagram of tower bottom section due to dead load

活载作用下，主梁和索塔的活载效应包络图相差较小。图6为主梁控制截面弯矩图，过渡墩处变化较大，4～6塔主梁活载最大弯矩依次最大增大14%、17%和10%。图7为主塔塔根弯矩，4 ～6塔的①塔根弯矩值依次增大20%、8% 和12%。

图6　活载作用下主梁控制断面弯矩Fig.6　Bending moment diagram of beam control section due to live load

均匀升温作用下，主梁和索塔内力随索塔数增多而增大。主梁弯矩变化较大的位置为辅助墩处，控制截面弯矩如图8所示，③号辅助墩处增加较大，4～6塔依次增大29%、18%和13%。塔根弯矩如图9所示，①号塔塔根弯矩增加最大，4～6塔依次增大50%、28%和22%。

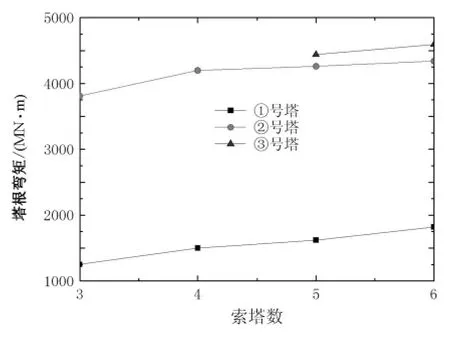
图7　活载作用下塔根弯矩Fig.7　Bending moment diagram of tower bottom section due to live load

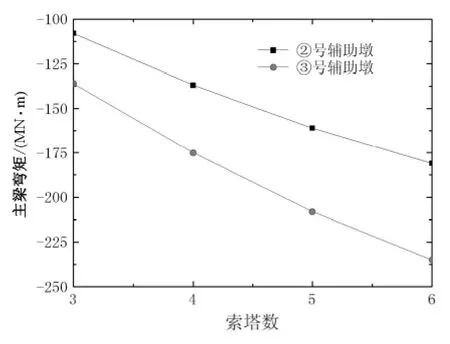
图8　温度作用下主梁控制截面弯矩Fig.8　Bending moment diagram of beam control section due to temperature

图9　温度作用下塔根弯矩Fig.9　Bending moment diagram of tower bottom section due to temperature

极限静纵风作用下，主梁和索塔内力随索塔数增多而增大。主梁弯矩变化较大的位置为辅助墩处，控制截面弯矩如图10所示，①号辅助墩处增加较大，4～6塔依次增大33%、25%和11%。塔根弯矩如图11所示，①号塔塔根弯矩增加最大，4～6塔依次增大13%、15%和2%。极限静横风作用下，结构内力相差不大，与索塔数无关。

图10　极限纵静阵风作用下主梁控制截面弯矩Fig.10　Bending moment diagram of beam control section due to longitudinal wind

图11　极限静纵风作用下塔根弯矩Fig.11　Bending moment diagram of tower bottom section due to longitudinal wind

通过比较发现，对结构内力状态而言，索塔数增加对主梁和索塔影响均较大，且索塔较为显著。

2.2关键力学特性

主梁竖向挠度和中塔主缆抗滑移系数是多塔协作桥关键力学参数。另外，中间索塔塔顶活载纵向位移也是反映关键力学问题的重要参数。索塔数增加时，结构更加柔细化，对上述参数产生影响。

主梁跨中活载最大挠度如图12所示，主梁挠度最大值为5.4 m，小于L/250 = 5.6 m。索塔数增加时，主梁挠度增大，最大增幅小于14%。此外，以6塔方案为代表对比不同主跨主梁挠度，第一主跨竖向挠度比二、三主跨小约36%，第二、三主跨之间相差不超过3%。

塔顶纵向位移如图13所示，索塔数增加时。边塔位移变大，增量最大为45%，而中塔略有减小，增量不超过2%。另外，边塔位移小于中塔，且索塔距对称中心越近，塔顶纵向位移越大。

图12　主梁竖向挠度Fig.12　Beam deflection diagram of all bridge due to live load

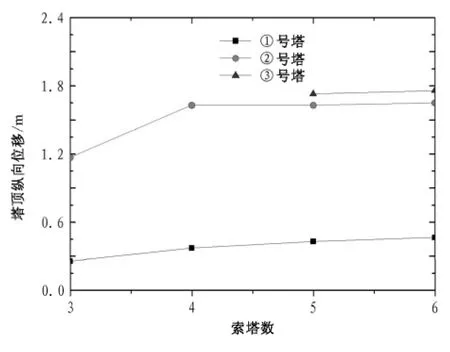
图13　塔顶活载纵向位移Fig.13　Displacement diagram of tower due to live load

主缆抗滑移系数按文献［11］计算，由文献［12］取μ=0.3，②号塔如图14所示。索塔数增加时，③号塔主缆抗滑移系数相差不大，②号塔依次下降36%、17%和5%左右，下降幅度趋向于稳定。究其原因，图15为抗滑移系数影响线，索塔数增加时，有效加载区域增多，抗滑移系数最不利影响区面积增大，所以主缆抗滑移性能下降，又因为当加载区域远离考察的索塔时，影响区面积很小，所以主缆抗滑移系数下降速度变小。

另外，③号塔主缆抗滑移性能优于②号塔，这体现了结构柔性特征。③号塔及相邻索塔在活载作用下产生纵向位移，使加载跨跨径变小，非加载跨跨径变大，从而降低了③号塔两侧主缆的不平衡力，抗滑移性能因此得到改善。此外，影响线曲线表明，②号塔的有效加载区域涵盖所有主跨，而③号塔仅仅涉及索塔两侧主跨及边主跨。

图14　②号塔主缆抗滑移系数Fig.14　Anti-slide factor of main cable of No.2 tower

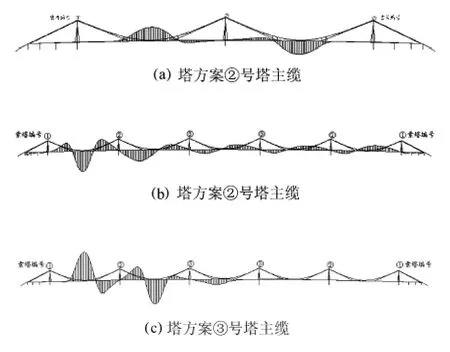
图15　中间索塔主缆抗滑移系数影响线Fig.15　Influence of anti-slide factor of middle tower

3　静力稳定性

多塔协作桥一阶弹性屈曲表现为中间索塔面外侧向弯曲失稳，且所有中间索塔基本同时失稳，3塔协作桥如图16(a) ;增加索塔刚度后，一阶弹性屈曲表现为②号塔处主梁压曲失稳，3塔协作桥如图16(b)。

计算表明，在恒载+横风+全桥均布荷载作用下，结构一阶弹性稳定系数最小，索塔数增加时，稳定系数变化趋势如图17所示。索塔数增加时，结构一阶弹性稳定系数降低，结构稳定性变差，与3塔相比，4至6塔依次减小8.3%，3.4%和0.9%。

图16　3塔协作桥一阶弹性失稳Fig.16　First order instability mode of three-tower cable-stayed suspension bridge

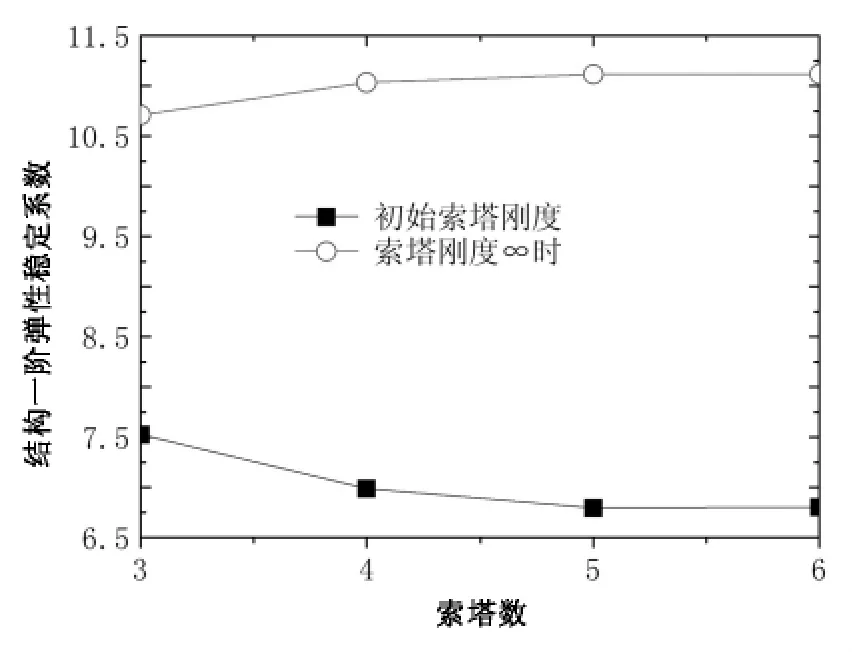
图17　多塔协作桥一阶弹性稳定系数Fig.17　First order instability factor of all bridge

增加索塔刚度后，索塔数增加时，结构一阶弹性稳定系数增加，与3塔相比，4至6塔依次增加3.0%，3.7%和3.8%。

4　动力特性

采用空间动力有限元分析，多塔协作桥各方案在成桥状态下的典型动力特性如表2所示。索塔数增加时，结构竖向和横向一阶对称和反对称弯曲模态出现次序不同，奇数个索塔时反对称先出现，偶数个索塔时对称先出现。因此，索塔数增加时，同一弯曲类型的频率以大小大小规律变化。一阶反对称扭转频率逐渐减小，与3塔相比，4至6塔依次减小7.7%，2.7%和1.1%。

按《公路桥梁抗风设计规范》(JTG/T D60-01-2004)对各方案的颤振特征参数进行计算，其值如图18所示。索塔数增加时，结构扭弯频率比和颤振稳定指数均增大。扭弯频率比，4至6塔依次增大5.4%，2.9%和2.2%;颤振稳定指数，4至6塔依次增大9.2%，6.0%和1.1%。可见，虽然扭弯频率比增大了，结构抗风要求仍然随索塔数增多而逐渐提高。

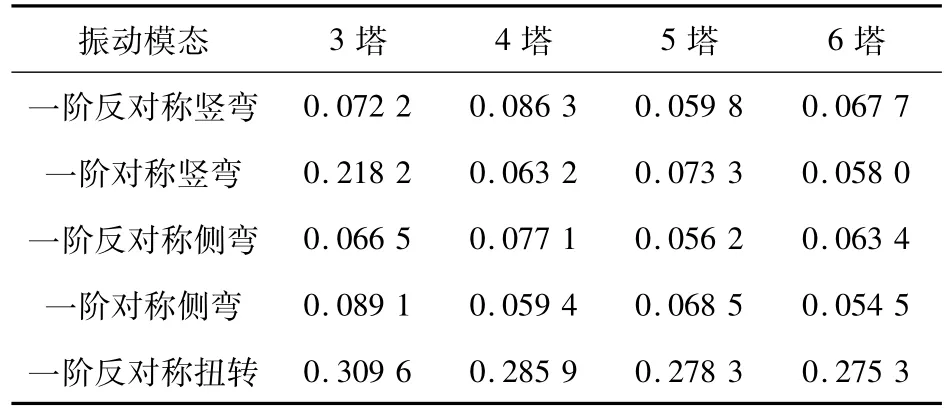
表2　多塔协作桥典型动力特性Tab.2　Typical dynamic characteristics of all bridges

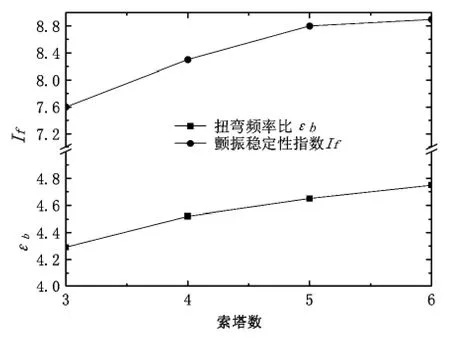
图18　多塔协作桥颤振特征参数Fig.18　Flutter characteristic parameter of all bridge

5　结论

1)索塔数对索塔内力影响较大，且边塔一般比中间索塔显著;对主梁内力影响相对较小，一般辅助墩处差异较为明显。

2)索塔数对主梁挠度影响较小，中间主跨挠度相近，且远大于边主跨;主缆抗滑移性能下降。

3)索塔数增加时，结构静力稳定性下降，抗风要求提高。

4) 4塔及以上协作桥结构的力学特性差异不大，且随索塔数增加逐渐趋于稳定。

参考文献

［1］杨进.悬吊斜拉组合桥结构应用于武汉市杨泗长江大桥的技术经济优势分析［J］.桥梁建设，2010(5) : 1-2.

［2］杨进.多塔多跨悬索桥应用于海峡长桥建设的技术可行性与技术优势［J］.桥梁建设，2009(2) : 36-39.

［3］许福友，张哲，黄才良，等.斜拉-悬吊协作体系桥工程应用及特点分析［J］.中外公路，2009，29(1) : 98-101.

［4］石磊，夏国平，苗峰.温度作用下斜拉-悬索协作体系桥静力分析［J］.沈阳建筑大学学报(自然科学版)，2010，26 (3) : 485-491.

［5］张哲，韩立中，万其柏.自锚式斜拉-悬吊协作体系桥的设计研究［J］.公路交通科技，2010，27(6) : 46-51.

［6］张哲，朱巍志，王会利.自锚式斜拉-悬索协作体系桥的方案设计［J］.桥梁建设，2009(4) : 50-53.

［7］夏国平，张哲，叶毅.斜拉-悬索协作体系桥的温度效应分析［J］.武汉理工大学学报(交通科学与工程版)，2009，33(5) : 892-896.

［8］张新军，孙炳楠，陈艾荣，等.斜拉-悬吊协作体系桥的颤振稳定性研究［J］.土木工程学报，2004，37(7) : 106-110.

［9］韩立中，张哲，张劲泉，等.大跨自锚式斜拉-悬索协作体系桥地震响应及减震控制分析研究［J］.武汉理工大学学报(交通科学与工程版)，2011，35(5) : 945-949.

［10］Haijun W，Yukitake S，Akira H，et al.Displacement characteristics of compound bridge of suspension bridges and cable-stayed bridges［C］//Cable-supported bridges challenging technical limits，Seoul，IABSE，2001: 86-87..

［11］浙江连岛工程建设指挥部，中交公路规划设计院，中国铁道科学研究院.特大跨径钢箱梁悬索桥设计指南(DB33/T 856-2012)［M］.杭州:浙江省质量技术监督局，2012.

［12］姜洋，肖汝诚，李扬，等.多塔悬索桥主缆与鞍座滑动失稳临界跨径［J］.同济大学学报(自然科学版)，2012，40 (3) : 331-337.

Study on mechanics property of multi-towers cable-stayed suspension bridges

ZHOU Yun-gang1，YANG Jing-hua2
(1.Tongji Architectural Design(Group) Co.，Ltd.，Shanghai 200092，China; 2.Unit 73049 of PLA，Suzhou，Jiangsu 215008，China)

Abstract:Four 3d finite element models for 3 to 6 cable-stayed suspension bridges are established by ANSYS software.The static property，dynamic property and static stability property of multi-tower bridge is analyzed and some characteristics are found.Furthermore，the key mechanics problems affected by tower-number，such as deflection of beam，longitudinal displacements of tower，anti-slide of main cable，are discussed.The result show that comparing study on mechanics property of 3 to 6 cable-stayed suspension bridge，bend moment of tower root increase maximally 50%，bend moment of beam increase maximally 33%，the anti-slide factor decrease maximally 36%，longitudinal displacement of middle tower decrease 2%，first order instability factor decrease maximally 8.3%，flutter stability index increase maximally 9.2%.The beam deflection of middle span is similar and larger than side span about 36%.Number of tower significant effect on its inter-force.

Key words:multi-tower cable-stayed suspension bridge; tower-number; span-number; static characteristics; static stability; dynamic characteristics

作者简介:*周云岗(1980-)，男，江苏淮安人，博士，工程师，主要研究方向为大跨度桥梁设计理论，Email:0710020026@tongji.edu.cn。

收稿日期:2014-02-28

文章编号:1007-791X(2015) 01-0088-07

DOI:10.3969/j.issn.1007-791X.2015.01.014

文献标识码:A

中图分类号:U448.25