巧妙设计数学练习?撞击学生思维火花

刘爱玲

摘 要：课堂练习是巩固知识、形成技能、发展思维、培养学生创造能力的重要途径。好的教学策略，优化的课堂训练，不仅能提高教学效率和教学质量，还能开发培养学生的创新能力，提高学生思维能力。课堂练习的设计应从趣味性、对比性、层次性、开放性、生活性的角度设计练习，练习设计要达到最优化，以期发挥练习在课堂中的最佳效率。

关键词：小学数学;课堂练习;巧妙设计

一、设计趣味性练习，促进学生积极思维

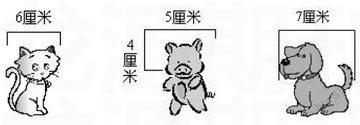
爱因斯坦有句名言：“兴趣是最好的老师。”说明兴趣对学习有着神奇的内驱动作用，能变无效为有效，化低效为高效。心理学研究也表明，当学生对某一学习内容的练习活动产生浓厚的兴趣时，他就会积极思考，大胆探索，从而优化自己的认知活动，促进学习。而趣味性的练习是培养学生学习兴趣的重要方法之一。因此设计练习时应注重题目的趣味性，使学生在愉快中获得知识，提高教学效率。例如，学习了“长方形、正方形的认识”后，我设计了课尾练习设计“猜猜边长是多少”。

（1）小猫后面藏了一个正方形，可以看见的这条边是6厘米，小朋友，你们知道看不见的三条边各是多少吗？请说出理由。

（2）小猪后面藏的是一个长方形，可以看见的两条边分别是5厘米和4厘米，小朋友你能猜出另外两条边是多少吗？请说出理由。

（3）小狗后面也藏了个图形。这个图形是个四边形，四个角都是直角，周长是24厘米，其中一条边是7厘米。你能想想它是什么图形吗？其他三条边的长度又是多少呢？为什么？

这种趣味性练习，不仅培养了学生的兴趣，还促进学生积极思维，又培养学生的数学表达能力。

二、设计对比性练习，启迪学生创新思维

前苏联教育家乌申斯基说过：“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切。”显然乌申斯基所强调的是一种思维能力，即比较思维能力。如在教完“较复杂的分数应用题”后，学生在解题时审题不够细，对应关系找不准，如何让学生认真过审题关呢？可设计如下练习。

（1）一根绳子长6米，用去2/3米，还剩多少米？

（2）一根绳子长6米，用去2/3，还剩多少米？

虽然只是一字之差，但解题方法和结果却大不相同。可见审题的重要性，以后不用老师强调，学生就会自觉审题，养成良好的审题习惯，同时能让学生在解题中发展学生的比较思维。

三、设计层次性练习，发展学生灵活思维

学生接受知识和巩固知识的过程依照由易到难，由浅入深的学习规律，考虑到不同层次学生的学习差异，因此，在课堂练习的内容上有层次、要求上有差异。我一般将课堂练习分为几个层次。

一类题面向全体学生，特别注意班级中的学困生，内容以本节课应掌握的基础题为主。

二类题面向班上中等以上的学生，题目的设计力求有一定的难度，指向学生的最近发展区。

三类题面向班上学有余力的优秀生，内容在二类题的基础上要有一定的发展，培养发散思维能力，鼓励超前学习。

要求学生在完成规定层次的练习后还能带着胜利的喜悦去做高一层次的练习。这样做才能让不同的学生在数学学习上得到不同的发展。如教学“简单的平均数应用题”时，我设计如下几个层次的练习，帮助学生巩固深化所学的知识。

（1）列式并计算。小红买来一本故事书，第一天看8页，第二天看6页，第三天看12页，最后一天看10页，平均每天看多少页？

（2）只列式不计算，并说理分析。气象小组在一天的2时、8时、14时、20时，测得温度分别是13度、16度、25度、18度。求这一天的平均温度。

（3）选择算式，并说明理由。玩具厂生产玩具，第一天生产180个，第二天生产200个，第三天上午生产120个，下午生产100个，平均每天生产多少个？

下面的哪种解法哪个对？哪个错？为什么？

（180+200+120+100）÷4

（180+200+120+100）÷3

（4）列式并计算，说明理由。哥哥和弟弟的平均身高是140厘米，已知哥哥身高是143厘米，弟弟身高是多少厘米？

以上几个层次的练习都是围绕总数、份数与平均数三个数量之间的关系来设计的。从易到难，从单一到综合，从顺向到逆向，题型多变，形式多样。通过练习，学生不仅掌握了基础知识和基本技能，还培养了灵活的思维能力。

四、设计开放性练习，挖掘学生创新思维

小学生由于知识及年龄的特点，往往反映出对问题的思考是单向的、一维的。因此，在数学课中，要经常设计一些开放式的练习题，强化训练，发展学生创新能力，让学生在知识的天空中自由翱翔，从中训练他们思维的深刻性、发散性和创造性，让他们主动地进行学习，加深对知识的理解和掌握，激发创造性思维。

例如，在教学“分数乘法”这一课时，我设计了下面练习：

有两根同样长的铁丝，第一根用去3/8米，第二根用去3/8，哪一根剩下部分长一些？

这道题的结论不明确，必须要根据铁丝原来的长度进行分析，我们不妨假设其原来的长度为a米。①当a>1时，a×3/8 > 3/8米，故第一根剩下部分更长一些;②当a=1时，a×3/8 =

3/8米，故两根剩下部分长相等;③当a<1时，a×3/8  < 3/8米，故第二根剩下部分更长一些。

又如 1/3×（   ）=（   ）×1/5 = 9×（   ）。

通过练习、比较，当它们的乘积为1时，答案最简便。这样就开阔了学生的思路，培养了学生的综合能力，挖掘了学生的创新思维。

五、设计生活性练习，培养学生发散思维

《数学课程标准》指出：“老师应该充分利用学生已有的生活经验，随时引导学生把所学的数学知识应用到生活中去，解决身边的数学问题，了解数学在现实生活中的作用，体会学习数学的重要性。”因此，数学练习的设计要联系生活实际，让学生把课堂上所学的数学知识运用于解决实现生活中的问题，让学生有成功体验，使学生感受到数学与日常生活的密切联系，从而激发学生学习数学的兴趣与动机，充分调动学生学习数学的积极性和主动性。

学了时间单位和长度单位后，可设计修改病句的练习：2015年2月29日，我到南京姑妈家。晚上我从永安出发，到南京可远了，足足有1000毫米，从9：00到早上6：00，坐火车用了6小时。姑妈来火车站接我，她还是那么年轻，身高162米，体重50克。见到姑妈我真高兴。

通过这样的练习，不但能增添课堂的气氛，而且能加深学生对数学的理解，学以致用，有很大好处，有效地促进了学生的发散思维。

总之，在数学教学中，巧妙设计发展性练习，积极创造条件，以学生发展为本，唤起学生的创新意识，培养学生的创新精神，提高学生的创新能力，使学生能时时撞击出创新的思维火花。

（作者单位：福建省永安市实验小学）