欧拉的“砝码问题”

蒋明玉

在历史上，论勤奋与对数学的贡献，很难有哪位数学家能够与欧拉相比，

欧拉往往能从被人们忽视的现象中提出有创新意义的数学问题，开辟数学科学中新的领域。

如天平的砝码是用天平称物的重要工具，那么准备怎样的一组砝码，在只允许将其放在天平的一端的情况下，可以保证称出砝码总克数以内的所有整克数的物品呢？

下面是欧拉研究过的“天平砝码最优（少）化配置问题”，同学们能独立试着做一做，并得出规律吗？让我们一起来试一试，

问题1：工人师傅用质量为15g的一个铁块制成4个质量不等的整克数的砝码，用这一组砝码，在只允许将其放在天平的一端的情况下，可以称出质量为15g以内的所有整克数的物品，这一组砝码分别是几克？

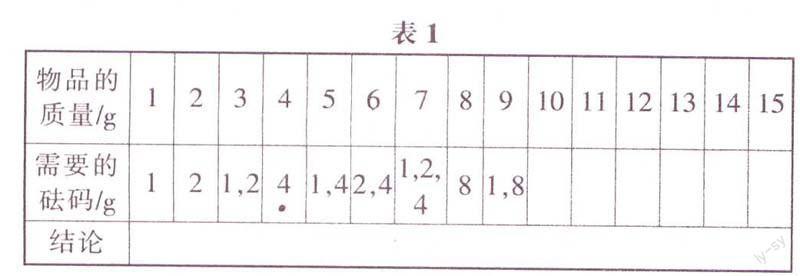
思考：可以从称1g的物品开始分析，完成表1，

从而得到结论：称质量为15g以内所有整克数的物品，只要准备质量为1g，2g，4g，8g这4个砝码，

如果到此为止，仅解决这一个问题，那么，就不算具有爱思考的好习惯了，让我们来分析这一组砝码，可以有下面几点发现：

1.这一组砝码的克数是一组有规律的数：1，2，2²，2³，

2，它们的和正好比这组数的下一项少1，即它们的和为：2⁴-1，

根据上面的发现，可以得到以下假设：

若有质量为1g，2g，2²g，2³g，…，2ⁿg的砝码，只允许将其放在天平的一端，利用它们可以称出质量小于2ⁿ⁺¹g的任何整克数的物体，

请你举例验证一下，

如果同学们再一起来解决下面的问题，会有新的发现的，

问题2：有一个质量为40g的砝码，现在把它加工成4个质量是不等整克数的砝码，允许将其放在天平的两端，可以用它们称质量为1g至40g之间的任意整克数的物体，这4个砝码的质量分别是多少？

思考：可以参考前面的研究过程来进行实验，具体步骤如下：

1.制表，2.填表，3.得到结果，4.研究结果，5.发现规律，6.进行验证，

不难发现，这4个砝码的质量分别是1g，3g，9g，27g称出质量为2g的物体，把质量为1g的砝码放在左边，质量为3g的砝码放在右边，利用3-1=2就可以了，质量为4g的物体可利用3+1=4称出质量为5g的物体可利用9-4=5称出，其他类似，

通过上面的6个步骤，相信你也能得到最后的规律：若有质量为1g，3g，3²g，3³g，…，3ⁿg的砝码，允许将其放在天平的两端，利用它们可以称出质量不超过（3ⁿ⁺¹）/2g的任何整克数的物体，

责任编辑：胡云志