初论几何图形

田载今

数学是研究数量关系（简称“数”）和空间形式（简称“形”）的科学。人类在认识客观世界的过程中，会遇到大量关于“数”与“形”的问题，小孩儿最早接受的数学启蒙教育，是最直观的“数”与“形”，他们往往从数手指头开始，认识了1、2、3、4、5等整数，在搭积木等游戏中，认识了三角形、正方形、圆、长方体等图形。提起数学，人们往往首先想到“数”，其实“形”在数学中是与“数”地位相当的，并且“数”与“形”有着紧密的联系。

一、几何图形是从物体形状中抽象出的数学概念

我们身边的物体都有各自的形状，几何图形是人们从丰富多彩的物体形状中抽象出的数学概念，例如，人们对满月、车轮、硬币等物体的形状进行抽象概括，发现这些物体的形状都符合“一中同长”的特点，即周边各点到中心一点的距离都一样长，为研究具有这一特点的物体形状，人们得出了圆的定义，即平面上到一个定点的距离等于定长的所有点的集合叫作圆，这个定点叫作圆心，定长叫作圆的半径，这里的圆，已经脱离了满月、车轮、硬币等物体的其他性质，只反映这类物体共同的形状特征。它是一种几何图形，恩格斯对几何图形的产生给出了精辟的总结：“‘形的概念完全来自外部世界，而非头脑凭空想出，对客观存在的物体形状加以比较，才得出‘形的概念。”

几何学是研究“形”的数学分支，它的英文单词为geometry，其中geo表示土地，metry表示测量，器物制造、土地测量等实际需要，是几何学产生的原动力，人们在长期的实践活动中。对来自现实世界的几何图形进行了深入研究，不断获取经验，发现规律，并加以系统整理。使得具有严密逻辑体系的几何学逐步形成，几何图形的形状、大小和位置等，是几何学研究的主要问题，按研究对象和研究方法的不同。几何学可分为欧氏几何、非欧几何、解析几何、射影几何、微分几何、代数几何等，其中，欧氏几何因古希腊数学家欧几里得而得名，它最早成型，是最基础的几何体系，而且对整个数学向公理化方向发展起了重要的推动作用，同学们在初中数学中所学习的几何知识都在欧氏几何范畴内。

二、几何图形的组成

几何图形形态各异，变化万千，有繁有简，最简单的几何图形是孤立的一个点，它只表示空间中的一个位置，而没有大小的规定，画图时笔尖接触一下纸就画出一个点，笔尖在纸上连续移动，所经过的不同位置分别对应空间中不同的点，这些点组成一条不间断的线，这就是“点动成线”，作为几何图形，任何线段（包括直线段和曲线段）都只计长短而不计粗细，线在空间中连续运动（平移、旋转等），其运动轨迹可以形成一个平面图形或曲面图形。这就是“线动成面”，封闭的平面图形或曲面图形都只计边界长短、面积大小而不计厚薄，面在空间中连续运动（平移、旋转等），其运动轨迹可以形成一个立体图形，这就是“面动成体”，封闭的立体图形一般只计边界长短、表面积大小、体积大小。

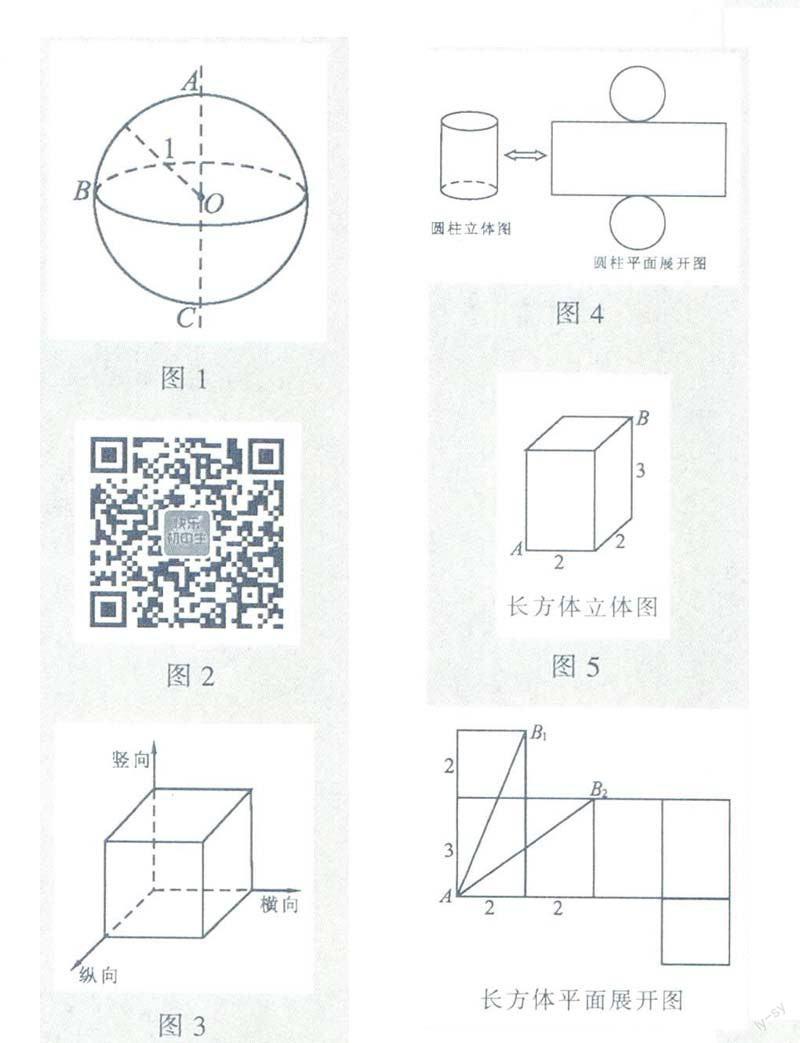
复杂图形可以分解为若干简单图形，点是组成几何图形的最基本的元素，每个几何图形都是符合一定条件的点的集合，例如，以点O为中心、半径为1的球面（如图1），是由空间中所有到点O的距离等于1的点组成的集合，它也可以看作半圆弧ABC绕直线AC旋转一周形成的曲面，

几何学中，平面是一个不加定义的原始概念，平面平如镜子，它不计厚薄，没有边界，可以向各个方向无限延伸。

几何图形可以分为两类：如果构成图形的点都在同一平面上，则这个图形属于平面图形，例如直线、三角形、四边形、圆等；如果构成图形的点不全在同一平面上，则这个图形属于立体图形，例如长方体、圆柱、球等，在欧氏几何中，以平面图形为主要研究对象的部分，叫作平面几何，以立体图形为主要研究对象的部分，叫作立体几何。

对于平面图形和立体图形，可以这样想象：

构成平面图形的点，是在一个不计厚薄的平面上运动，点的运动轨迹上的任一位置，由横、纵两个方向上的位置所确定，这类似于在平房教室中，每个学生的座位由座次表上的横向排号和纵向列号两个数所确定，这两个方向称为两个维度，所以平面图形也叫二维图形，现在常用的二维码（如图2），是按一定规律在平面上黑白相间地排列而得到的图形，它记录了特定的数据符号，由于它是用平面图形表达信息的，所以叫作二维码。

构成立体图形的点，是在一个像盒子一样的空间里运动，点的运动轨迹上的任一位置。由横、纵、竖三个方向上（如图3）的位置所确定，这类似于在有不同楼层的剧场中。每个观众的座位由入场券上的横向排号、纵向列号和竖向楼层号三个数所确定，这三个方向称为三个维度，所以立体图形也叫三维图形，我们能直观感受到的外部空间是三维空间，所以三维图形也常被称为空间图形，通常所说的3D电视，就是能使画面产生立体视觉效果的电视，

平面图形与立体图形在一定条件下可以互相转化，如图4，圆柱是立体图形，把组成它的各个面平铺开来，所得展开图是平面图形：反过来，把圆柱的平面展开图折起。各个面又围成立体图形，认识立体图形时，通常先从它包含的平面图形人手，这种研究方法是“降维处理”，但是，不是任何立体图形都有平面展开图，例如，球的表面是一个完整的曲面，它不能严格地展开成平面图形，我们只能设法得到其平面近似展开图，绘制世界地图时，会用到这种近似展开方法。

例1如图5，一只蚂蚁在长方体上的点A处，它要沿我们能看到的面爬到点B处，最短路程是多少？

解：观察图5，根据经验可知，蚂蚁要想以最短路程从点A处爬到点B处，至少要经过长方体的两个面（即经过正面与上底面或经过正面与右侧面），画出长方体的平面展开图（如图6），图5中的点B对应图6中的B₁、B₂两个点，两个点之间的最短路径是连接这两个点的线段，比较线段AB₁和线段AB₂，通过测量可以发现AB₁>AB₂，故在图5中，从点A处出发，经过正面与右侧面到达点B处的路径（对应图6中的线段AB₂最短，按图中标注的尺寸，可以通过测量、计算得到最短路程为5。

三、直线是原创几何图形

几何学有严格的逻辑顺序，如果要给一种几何图形下定义，定义中出现的其他图形必须是此前已明确的概念，因此，在逻辑链条的起始端，必然要有一些只作描述而不加定义的原始几何图形，它们是以后衍生出其他一系列几何图形定义的基础，点、直线、平面等都是原始几何图形。

直线无定义，对它只有描述性的解释，如像一根拉紧的细线，没有弯曲之处，不计粗细，可以向两个方向无限延伸等，直线概念既来自于实际原型（如拉紧的细线等），又高于实际原型，其中包含了人类丰富的想象力（如无限延伸等），直线是动点朝两个相反的方向移动的轨迹，从运动方向的角度看，沿一条直线的运动最简单，例如物体在自由下落的过程中，方向始终竖直向下，物理中把这类运动称为直线运动。

一条直线上有无数个点，这些点有序地排列在直线上，中间不存在“空位”，这体现了直线上点的有序性和连续性，人们正是利用这些性质发明了数轴这一表示实数集合的直观模型。

无数次实践验证了一个基本事实：在空间中任意选取两个点，经过它们能且只能画出一条直线（如图7），人们把它归结为一条公理（即直接承认的真理）：两点确定一条直线，这里的“确定”包含了“存在性”（一定有过这两个点的直线）和“唯一性”（过这两个点的直线只有一条），几何学中，像这样有双重含义的“确定”广泛地存在着，如：不在同一直线上的三个点确定一个圆（如图8），不在同一直线上的三个点确定一个平面（如图9），

有了直线这一原始几何图形，就可以用它定义射线和线段这两种基本几何图形，直线上的一个点和它一侧的那一部分叫作射线，直线上的两个点和它们之间的那一部分叫作线段，显然，射线无限长，它表示了一个确定的方向，线段有长度，“两点之间线段最短”是几何学中的又一条公理，一条线段的长度就是线段的两个端点之间的距离。

例2空间中有n个点，其中任意三个点不在同一直线上。以这些点为端点的线段共有6条，

（1）求n的值，

（2）设A、B、C是这n个点中的任意三个，线段AB、AC、BC之间有什么关系？

解：（1）以这n个点中的任意两个为端点，可以连出一条线段，所以每个点均可与另外（n-1）个点连出（n-1）条线段，以两个点为端点的线段仅有一条，所以线段的总条数为

（2）如图10，因为A、B、C三个点不在同一直线上，线段AB是A、B两个点之间的最短路径，A→C→B是从点A到点B的另一条路径。所以AB

线段是直线上有限长、不间断的一部分，它的长度容易理解，由线段组成的几何图形属于直线形，例如三角形、四边形、五边形等，直线形的度量和计算（周长、面积等）建立在线段长度的基础上，例如三角形的周长C=a+b+c。

直线有一个特性是处处不弯曲，有些几何图形不具有这种性质，例如圆弧是处处弯曲的线，它属于曲线，含有曲线的几何图形属于曲线形，曲线形的度量和计算要比直线形复杂，例如推导圆的周长公式和面积公式要比推导三角形的周长公式和面积公式难得多，

能否通过“化曲为直”使曲线形的计算变得容易呢？我们看看魏晋时期的数学家刘徽是怎么做的，如图11，刘徽先把圆周六等分，连接各等分点，得到圆内接正六边形；在此基础上，再把圆周十二等分，连接各等分点，得到圆内接正十二边形……继续下去，使圆内接正多边形的边数不断加倍，则圆内接正多边形的面积就越来越接近圆的面积，正多边形是直线形，它的面积相对容易计算，通过计算边数不断加倍的正多边形的面积，可得到圆的面积越来越精确的近似值，可以想象，当边数充分大时，圆内接正多边形与圆几乎重合，刘徽用这种“割圆术”计算出圆的面积高精度的近似值，并求出圆周率的近似值3.14，这在当时是非常辉煌的成就，可以发现，刘徽的“割圆术”是通过无限细分的方法，使微小的圆弧段转化为与之极为相近的微小线段，这种“化曲为直”的方法与思想。和后来出现的微分方法、极限思想高度一致。

几何图形中蕴涵了丰富的数学知识，随着学习的深入，同学们会不断提高对它们的认识。

责任编辑：潘彦坤