应用型本科管理类专业运筹学课程体系的建设
2015-05-30项芹
项芹

[摘 要]运筹学作为一门应用性的学科,在教学过程中,如何提高其实用性及学生的学习兴趣,引起了越来越多的关注。本文主要针对应用型本科管理类专业这一特定的目标,试图建立运筹学的课程体系,对教学内容以及学时进行了规划,并对教学思路进行了一定总结,以期为应用型本科层次运筹学的教学提供借鉴。
[关键词]运筹学; 应用型;课程体系
[DOI]10.13939/j.cnki.zgsc.2015.15.128
1 引 言
運筹学是运用定量化的方法,对所研究的各类管理优化问题建立数学模型进行求解,然后进行定量和定性分析,为决策者做出合理的决策提供科学的依据。运筹学是管理类专业的一门重要专业基础课。
作为一门应用性的学科,要求学生具备一定的数学基础,掌握各个组成分支的基本算法,更重要的是引发同学们学习兴趣,能够建立数学模型应用到生活工作实践中去。在笔者运筹学的学习及现在的教学实践中发现,运筹学作为应用数学的一个分支,很多同学特别是数学理论知识不是很扎实的同学普遍觉得运筹学的学习太难理论性太强,提不起学习兴趣,很难将其利用到自己的工作实践中去。而作为管理类专业的学生,实际应用才是学习本课程的主要目的,因此该课程的教学应与学生所学专业相结合,在数学算法够用的基础上,加强其应用发面的教学。
在本文的研究中,旨在将运筹学的教学跟学生所学专业相结合,重新建立适合应用型本科管理类专业运筹学的课程体系,优化教学内容,激发学生学习兴趣,在掌握一定算法的基础上,关键能够学以致用。
2 课程体系建设
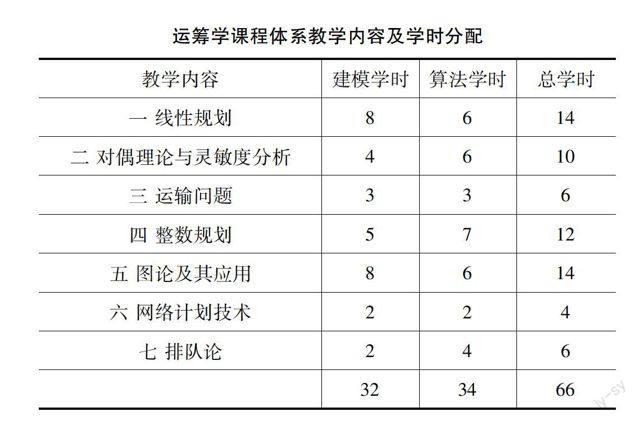
自从20世纪30年代以来,运筹学经历了不断地发展,分支越来越细化完善,包含多个分支:数学规划(又包含线性规划、非线性规划、整数规划、组合规划等)、图论、网络流、决策分析、排队论、可靠性数学理论、库存论、对策论、搜索论、模拟等。在本科阶段的教学中,作为管理类专业的本科层次的学生,一方面学要建立运筹学的基本概念,掌握运筹学的基本思想,另一方面要能运用运筹学的基本思想解决实际问题也就是能根据实际问题建立数学模型。在有限的教学学时内,不能做到每个分支讲解得面面俱到,而是应根据专业及学生基础的要求做到有重点的选择,建立适合不同类型专业不同基础的学生的运筹学课程教学体系。下表体现了笔者在应用型本科层次66个学时的教学课时中对教学内容的选择及学时的安排,将运筹学的教学分为建模和算法两个模块,两个模块在教学的过程中相互交叉,穿插进行,跟传统的运筹学教学相比,更强调了建模的教学也就是运筹学的实际应用,建模的学时占到了总课时的近一半,同时也注意基本算法思想的讲解,作为本科层次的同学来讲,算法是基础,只有将基本算法的思想掌握了,才能进一步应用到生产实践中去。
现以第一部分线性规划和第五部分网络规划为例,对本课程体系讲解的主要侧重点及本课程体系与管理类相关专业的联系做说明。第一部分线性规划是运筹学的课程体系必选的内容,一方面线性规划方法是实际应用最广泛、最基础的方法之一,另一方面线性规划容易理解和掌握,使得初次接触运筹学的同学们更容易形成运筹学的基本思想。本章一个重点为线性规划模型的建立,通过各种实际应用举例使学生掌握建立线性规划模型的有关技巧,占到了线性规划部分总课时的一半以上。建模的主要应用领域为生产计划问题、运输问题、劳动力安排问题、存储问题、投资问题等,都是与管理类专业背景密切相关的实际应用问题。同时在分析单纯形法算法思想的基础上让学生了解并掌握单纯形法的基本步骤及算法思想。
第五部分图论,是本课程体系包含的另一个重点内容,同样在讲课的过程中始终围绕其实际应用进行讲解。图论起源于18世纪的欧拉环游问题,今天图论的理论和方法已经渗透到物理、化学、生物遗传学、心理学、经济学、社会学等学科中的多个社会领域。图论中所谓的“图”是指某类具体事物和这些事物之间的联系。如果我们用点表示这些具体事物用连接两点的线段表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。在本课程体系中,侧重于通过图论用比较直观的方法解决线性规划中遇到的一些实际问题,比如生产计划问题、资源分配问题、投资问题等,跟第一部分线性规划问题内容相呼应。同时也讲解基本算法思想,包括最短路径问题、最长路径问题、最大流、最小代价流等基本算法。
3 教学思路改革
本课程体系在建设的过程中跟传统的课程体系相比较更加注重建模的教学,也就是实际应用的操练。因此在教学过程中,建模始终穿插其中,通过解决生活生产实践中的问题,建立模型引出算法,讲解算法并求解。现以线性规划的讲解为例进行教学思路的说明。
线性规划问题是同学们接触运筹学的开始,如何让同学们觉得运筹学跟他们的生活贴近,而不是很抽象难懂,是应用型本科运筹学教学中引起同学们学习兴趣的关键。如果一开始就直接讲解抽象的单纯形法,必然会使很多数学基础不太好的同学会失去对运筹学的学习兴趣。因此线性规划讲解通过实际问题引出,建模型,引出线性规划的基本概念,在求解过程中,先由较容易理解的图解法及典型方程组引入,理解了基本概念以后,最后再讲单纯形法的算法,使得同学们有一个从具体的实际问题、形象的图解法到抽象的数学算法的过程。如右图所示。
4 结 论
本课程体系的建设主要针对应用型本科管理类相关专业,通过强化运筹学建模的学习,目的在于弱化同学数理基础,提高同学们的学习兴趣,并能够将运筹学与所学专业相结合,提高运筹学的应用性。
参考文献:
[1]傅家良.运筹学方法与模型[M].上海:复旦大学出版社,2013.
[2]秦明森.运筹学在物流管理中的应用[J].物流技术,2003,(10):52-53.
[3]刘德海.应用型人才培养模式下“运筹学”教学改革研究[J].东北财经大学学报,2011(6):35-37.
[4]左元斌.管理类专业运筹学课程教学改革探讨[J].盐城工学院学报(社会科学版),2007,(4):90-92.
[5]韩伯棠.管理运筹学[M].北京:高等教育出版社,2000.
