基于矢量奇异值分解的DOA估计方法及其改进

陈章 卫武迪

【摘要】 对相干信号的波达方向（DOA）估计是空间超分辨谱估计的热点。在均匀线性阵列模型下，特征矢量奇异值分解法（ESVD）能够很好的对相干信号进行DOA估计，但是当相干信号和非相关信号同时存在时，ESVD并不能对全部信号进行DOA的估计。本文通过对ESVD算法的理论分析后，选取经过加权处理的特征向量来构造新矩阵，再利用奇异值分解得到信号的噪声和信号子空间，从而进行DOA估计。理论分析和计算机仿真表明该改进算法（MESVD）解决了ESVD算法在相干信号和不相关信号同时存在不能正确进行DOA估计的问题，估计精度与空间平滑算法（FBSS）相当。

【关键词】 DOA估计 相干信号 奇异值分解 空间平滑

Abstrct：The direction of arrival （DOA） estimation of coherent signals is a hotspot issue of High-resolution spatial spectrum estimation.Under the Uniform Liner Array model，the Extended Signal Value Decomposition（ESVD） algorithm can estimate the DOA of coherent signals exactly.However， when the coherent and non-related signals existing at the same time，ESVD fails to estimate all DOA of the signals. Through the theoretical analysis of the ESVD algorithm.a modified algorithm is proposed which select the weighted eignvector to construct a matrix for subspaces estimation. Theoretical analysis and computer simulation indicate that the improved algorithm （MESVD） solves the defect of the ESVD algorithm that it can not estimate all DOA of the signals when the coherent and non-related signals existing at the same time. The estimation accuracy of MESVD resembles the FBSS algorithm.

Key words：DOA estimation，coherent signals，Singular value decomposition，Spatial smoothing

一、引言

陣列信号的波达方向（DOA）估计一直都是空间谱估计研究的重要问题。传统的子空间类算法如MUSIC等不能直接对相干信号进行精准估计，这是因为相干信号会导致信源协方差矩阵的秩亏损，从而使信号特征向量发散到噪声子空间中去，MUSIC谱就无法在波达方向产生波峰。处理相干源估计问题基本上有两类方法[1]：一是降维处理，代表算法有空间平滑算法、矩阵分解算法以及矢量奇异值法等。二是非降维处理，代表算法有Toeplitz方法、ML算法等。本文重点研究的是降维处理中的奇异值分解法（ESVD）[2]，该算法的重点是对接收数据协方差矩阵进行特征值分解，用最大特征值对应的特征矢量重构矩阵并对其进行奇异值分解，找出噪声子空间和信号子空间。ESVD虽然能对相干信号进行DOA估计，但在相干信号和非相关信号同时存在时，该算法就不能对全部信号的DOA进行准确估计。针对这一问题，本文在对ESVD算法进行理论分析和研究后对其进行改进，仿真结果论证了改进后的算法（MESVD）解决了上述问题。

二、信号模型及传统算法

考虑由N个阵列组成均匀线性阵列，阵列间距为d。假设M个远场窄带信号（M

式中U是左奇异矩阵，V是右奇异矩阵，Λ是由奇异值组成的s×r维矩阵。理想状态下Y的奇异值个数应该等于信号源数M，左奇异矩阵中小奇异值对应的矢量张成噪声子空间，大奇异值对应的矢量张成信号子空间，对照MUSIC方法就可对信号进行DOA估计。

奇异值分解算法采用的是最大特征值对应的特征向量来重构矩阵，在信号完全相干的情况下能够对入射信号DOA进行很好的估计。但是，通常接收信号不是完全相干的，当相干和非相关信号同时存在时，特征值分解得到的最大特征矢量肯定不能包含所有的入射信息。按照ESVD算法，只取其中最大特征矢量很难完成全部信号的DOA估计而出现漏估的情况。很容易联想到的是将所有大特征值对应的特征矢量加权处理来重构矩阵，该加权重构的矩阵就能包含入射信号的所有信息。现将算法进行改进：用（7）式中的所有大特征矢量求和后的平均值eavg 来构造矩阵Y：

对新构建的矩阵Y进行奇异值分解得到信号和噪声子空间，再参照（4）式就可以对信号DOA进行估计。

四、仿真分析

模拟4个等功率信号分别从-15°、12°、30°及60°方向入射，其中60°方向信号与其它三个彼此完全相干的信号不相关。阵元数为15。信噪比为10db，快拍数为500。分别用最大特征值对应特征矢量、次大特征值对应特征矢量及本文提出的加权处理的特征矢量来重构矩阵进行仿真，加入空间平滑算法进行对比。

（选取信号最大特征矢量构建矩阵Y）

从图1可以看出，ESVD算法成功估计出3个相干信号，在非相关信号估计上出现了丢失，这是因为此时信号协方差矩阵的大特征值不止一个，理论分析與仿真果一致。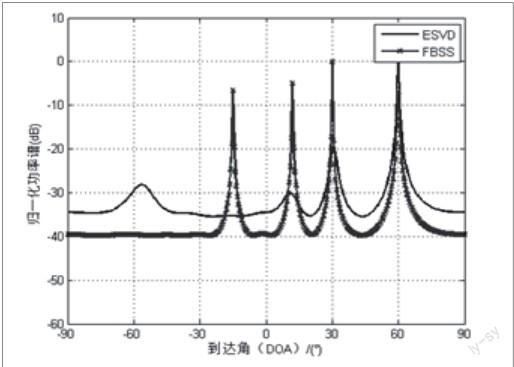

（选取信号次大特征矢量构建矩阵Y）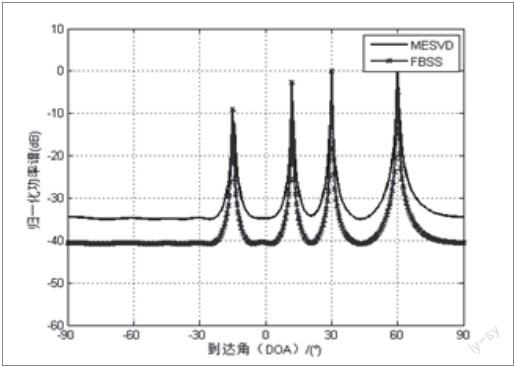

从图2可以看出，ESVD算法仅成功估计出60°方向的信号，与之前的结果相反，仿真结果表明了不同大特征矢量包含信息是不同的，只用某单一大特征矢量来估计信号是不能完全估计全部信号的。

从图3可以看出，改进算法成功对四个信号的DOA进行了估计，估计精度与FBSS相当，解决了传统特征矢量分解法不能正确估计相干信号和非相关信号同时存在的情况。

五、结论

通过对ESVD算法的理论研究与分析后对其进行了改进，仿真结果表明改进后的算法解决了ESVD在相干信号和非相关信号同时存在时不能正确估计信号DOA的问题，加入FBSS作对比，仿真表明两者精度相当。

参 考 文 献

[1]王永良、陈辉等.空间谱估计理论与算法.北京：清华大学出版社，2004.

[2]高世伟，保铮.利用数据矩阵分解实现对空间相干源的超分辨处理。通信学报，1988，9（1）：4-13.[3]R.O.Schmidt，Multiple Emitter Location and Signal Parameter Estimation，IEEE Trans，AP，vol.34-3，Mar， 1986，pp.276-280.

[4]张贤达.现代信号处理。北京.清华大学出版社，2003.

[5]Shan T J，Wax M.Adaptive beamforming for coherent signals and interference.IEEE Trans Acoustic Speech and Signal Processing，1985，33（3）：527-536.

[6]胡晓琴.超分别空间谱估计技术应用基础研究. 长沙：国防科学技术大学博士论文，2009.