例谈数形结合思想在数学解题中的应用
2015-05-30丁伟
丁伟
【摘要】 近年来,中考中的数学题综合性越来越强,往往不是就几何考几何就代数考代数,而是将代数与几何相结合,这也在一定程度上增加了学生解题的难度.因此教师在教学时应注意用数形结合的思想引导学生思考,培养学生的辩证思维和发散思维.数形结合有助于化抽象为具体,化难为易,能帮助学生解题.
【关键词】 数学教学;数形结合思想;解题应用
“数”与“形”是数学的两大板块,但是这两个板块并不是孤立的. 代数是严谨而细腻,几何是形象而直观,如果我们能扬数之长,取形之优,使得代数与几何紧密结合起来,相互转化,相互促进,这样我们用数学来解决问题将会更加简单,而且数学也不会是枯燥乏味和单一的,而是生动形象和多样的,这就是“数形结合”的思想方法所能展现的无比优越性. 同时用数形结合的方法来解决数学问题又有助于培养学生的辩证思维、发散思维和创新思维.
我国古代数学家也早就将代数和几何结合起来,解决了许多长期解决不了的问题,例如尺规作图三大不可能问题,就通过代数方法得到圆满解决. 如今,通过实践和探索,我体会到在数学教学中用“数形结合”的思想指导学生思考,用这个技巧来训练学生解题,对激发学生的学习兴趣和思维能力的培养具有很大的优越性. 下面就数形结合思想在中学数学解题中的应用来举例说明.
一、数形结合思想在概念中的应用
1. 为避免学生死记硬背, 利用数形结合的思想进行对概念公式的理解是有效措施之一.
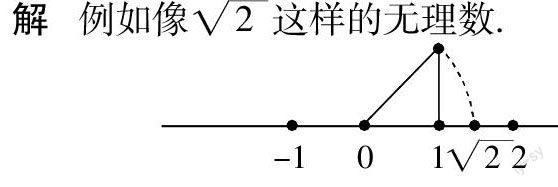
例1 如何理解实数与数轴上的点的一一对应关系,对给定的无理数是否在数轴上能像有理数那样找到它对应的点, 对这一概念的理解有必要利用数轴这一图形来描述这样的点.
这一题的原型是初一上册课本上在数轴上画出无理数的点,而且无理数给的是面积为2的正方形的边长. 在这里就要求学生能准确画出无理数的点还是很困难的,关键是掌握技能和方法,同时还要学会引申,学会画面积为8的正方形的边长等,在此基础上再让学生来感受实数与数轴上的点一一对应就更加形象直观了.
2. 数形结合能帮助学生深化对相关概念之间关系的理解,使学生深入掌握概念,是发展数学思维能力的有效方法之一.
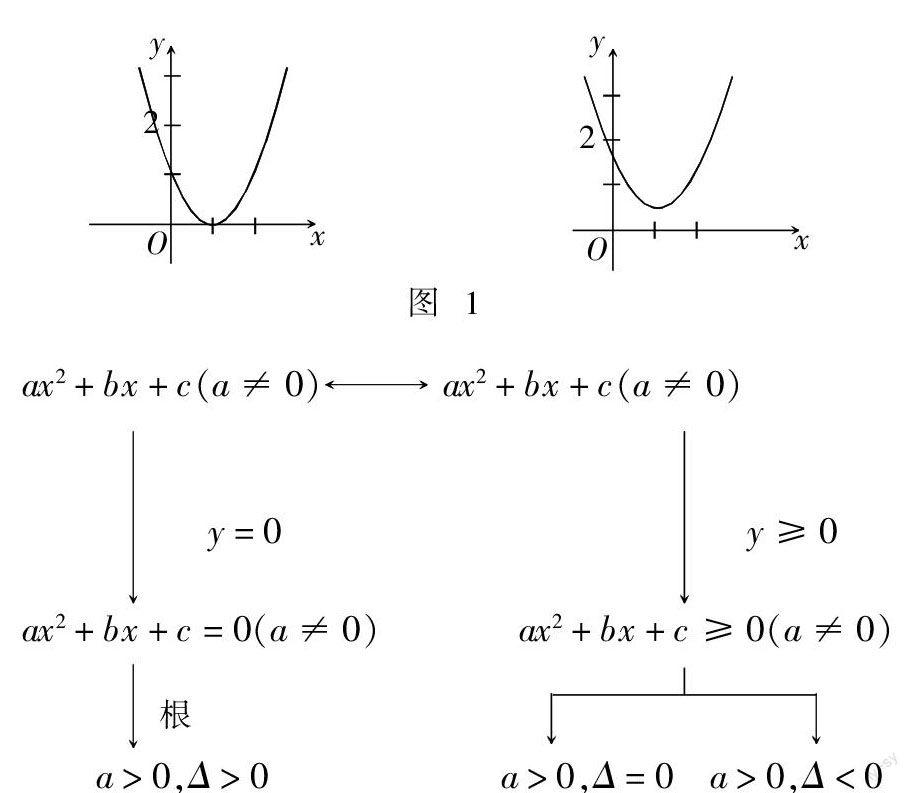
例2 建立二次函数、一元二次方程、一元二次不等式、一元二次三项式各概念之间的联系框架图. 如图1.
学生在学习代数式、函数、方程以及不等式时往往会孤立地思考问题,这样就忽视了其中的共性. 然而若是通过函数图像来解决问题就能从根本挖掘到问题的本质,同时解决问题既快速又准确,提高了解题速度与效率.
二、数形结合思想在几何问题中的应用
运用数形结合思想来解题很大一部分是运用图形方法解决代数问题,但其实还有一些需要用代数法解决几何问题,这样就把抽象的几何问题变得具体明了了,而且解题更加严谨.
例3 证明: 圆内接矩形以正方形的面积最大.
分析 要证明的是最值问题,如果用几何问题去解,则不容易找到解题思路,若把它转化为代数问题可用代数中求最值的方法去求解.
总之,运用数形结合的思想方法指导学生解题一方面可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质;数形结合也为培养具有创新精神和实践能力,能够适应社会发展需要的高素质人才的时代教育任务奠定了基础,因此它在中学数学教学中起着举足轻重的作用.
