“三角形复习课”的教学思考

晏玉香

数学课的教学设计，我们既要尊重学生的认知规律，又要尊重知识本身的生长规律，要在知识呈现的过程中，让学生体会知识的生长点，体会知识的相关性，帮助学生以逐渐生成的方式内化为自己的认知;在解决问题的过程中让学生体会解读条件的必要性，解决问题的方法往往就隐藏在条件背后. 初三“三角形”的复习给我们提供了一次教学生分析问题，帮助学生形成良好思维品质的机会.

一、从整理知识结构说起

复习课难上，难在学生都学过这部分内容，已经没有新鲜感，尤其是这些数学定义、性质、判定、推论，但是这些知识点又是解决综合题必备的知识基础，那么怎么样让学生既复习好这部分知识，又不枯燥无味呢？

我在设计时，先在黑板上画一个三角形，让大家回忆一下与这部分相关的知识点，学生很快就会说出：内角和180°，勾股定理，高线，中线，角平分线，特殊的等腰三角形，直角三角形，两边之和大于第三边.

学生很快地唤醒了这部分记忆，只是这是很零散的知识点，下面让学生试着归类，提高学生知识的整合能力，也是让学生自主地在脑海中构建知识体系. 在教师的引导和学生的努力下，不难一起整理出三角形这一部分的知识结构图.

概念及性质（由三条不在同一条直线上的线段首尾顺次相接组成的封闭图形，三角形具有稳定性）

图形元素（三个顶点，三条边，三个内角，六个外角）

分类

三边关系：两边之和大于第三边，两边之差小于第三边.

内外角关系：三角形的一个外角大于与它不相邻的任何一个内角;三角形的外角等于与它不相邻的两个内角的和.

边角关系：三角函数，勾股定理.

重要线段：高线、中线、角平分线.

二、从具体的知识点联想其各种应用

三角形的角平分线是一条非常重要的线段，那么角平分线究竟有哪些常见的应用类型呢？笔者没有像传统的课堂一样，直接呈现三角形几种常见应用的例题，这样直接“喂食”的方式没有新意，而且很难被学生真正接受，因此笔者也是让学生先回忆与角平分线相关的常见的应用. 这时学生会积极思考从脑海中快速搜索，比如三角形角平分线的性质，角平分线与等腰三角形、平行线结合的知二求一，由角平分线轴对称变换构造等腰三角形，这时在教师的提示下，也可以总结出根据角平分线截长补短构造轴对称型全等，下面再展示如下几个例题，在总结完三角形的应用的基础上看这些例题，也会更加有针对性.

1. 角平分线的性质，即角平分线上的点到角的两边距离相等.

在四边形ABCD中，BC > BA，AD = DC，BD为∠ABC的角平分线. 求证： ∠A + ∠C = 180 °

分析   可以过点D分别作AB和BC的垂线段，证明两直角三角形全等，当然此题也可以用截长补短构造轴对称型全等.

2. 平行线、等腰三角形、角平分线的知二求一.

如图所示，在△ABC中，已知∠B和∠C的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E ，若DE长15 cm，求线段BD + CE的长.

分析   由题目已知，角平分线和平行线的结合出现了两个等腰三角形，因此把BD和CE分别转移到DF和EF.

3. 根据角平分线截长补短构造轴对称型的全等三角形.

如图，△ABC中，AD平分∠BAC，AB + BD = AC，求∠B ∶ ∠C的值.

分析   由题目已知中的AB + BD = AC，这是线段和差关系，很容易想到截长补短的辅助线，而且还有角平分线，因此为构造轴对称型全等提供了条件，此题可以在AC上截取AE使得AE = AB（截长），或者延长AB至F，使得AF = AC（补短）.

4. 由角平分线轴对称变换构造等腰三角形.

已知：等腰直角三角形ABC中，∠A = 90°，AB = AC，∠B的平分线交AC于D， 过C引 BD的垂线交BD的延长线于E.

求证：BD = 2CE.

分析   等腰直角三角形是一类非常重要的三角形，为旋转提供便利条件，同时题中也给出了角平分线以及CE与BE垂直的条件，因此此题延长CE与BA的延长线相交于F，这样出现了一组轴对称的直角三角形，从而得到一个等腰三角形.

三、由具体的问题分析其背后隐藏的知识点

刚才是由一个知识点联想其各种应用，下面反过来，从一个具体的应用挖掘其背后隐藏的知识点.

问题   已知：如图，在△ABC中，D为BC中点，DE⊥DF，DE交AB于E，DF交AC于F，问：BE + FC与EF的关系？

挖掘题目背后的知识点：

1. 由DE⊥DF可想到：

（1）直角三角形的所有性质及相关结论;

（2）直角三角形可以经过轴对称变换得等腰三角形.

2. 中点联想到的知识点有：

（1）中点定义.

（2）倍长中线（即构造中心对称型全等）.

（3）中位线定理.

（4）直角三角形斜边上的中线等于斜边的一半.

（5）三角形的一条中线将三角形的面积分成相等的两部分.

（6）和等腰三角形结合的三线合一.

3. 直角顶点恰好是一条线段的中点可以联想到“半角模型”：两次翻折构造全等.

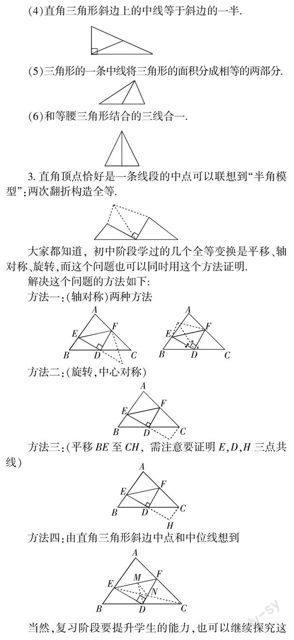
大家都知道，初中阶段学过的几个全等变换是平移、轴对称、旋转，而这个问题也可以同时用这个方法证明.

解决这个问题的方法如下：

方法一：（轴对称）两种方法

方法二：（旋转，中心对称）

方法三：（平移BE至CH，需注意要证明E，D，H三点共线）

方法四：由直角三角形斜边中点和中位线想到

当然，复习阶段要提升学生的能力，也可以继续探究这个问题.

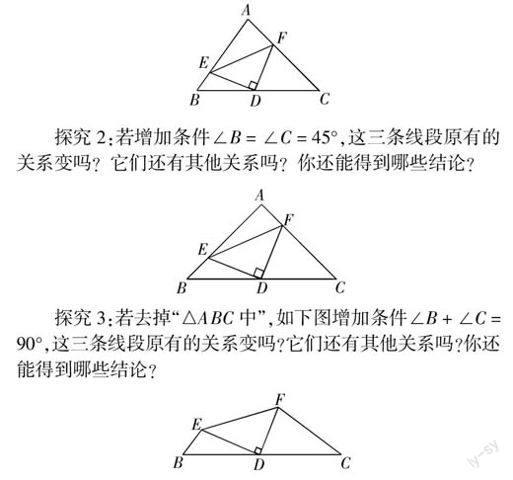
探究1：若增加条件∠B + ∠C = 90°，这三条线段原有的关系变吗？它们还有其他关系吗？你还能得到哪些结论？

探究2：若增加条件∠B = ∠C = 45°，这三条线段原有的关系变吗？它们还有其他关系吗？你还能得到哪些结论？

探究3：若去掉“△ABC中”，如下图增加条件∠B + ∠C = 90°，这三条线段原有的关系变吗？它们还有其他关系吗？你还能得到哪些结论？

题目的条件决定了结论，也给我们提供了解决问题的方法，这个问题意在让学生体会挖掘题目条件的必要性以及几何问题的分析方法，同时对条件的不同关注可以让我们找到解决问题的不同方法——一题多解. 这道题虽然不难，但对于提升学生的知识使用能力而言，却不失为一道好题，它具有基础性、代表性、生长性，既可以进行知识间的纵横联系，又能进行一题多解、一题多变，使学生对知识的相关性有了深入的体会.

初三复习时间紧张有限，作为老师，我们应该怎样改善学生的学习方式？怎样尊重知识的生成过程？如何在有限的时间让我们的学生收获更多？这是我一直思考的问题.其实我们只需要站在学生的角度，做到每节课设计的问题既不能脱离学生实际，又不能脱离知识本质;既要关注问题的深刻性，又不能忽视学生的可接受性;既要顺应知识的生长规律，又要关注学生的思维成长规律. 我们要通过帮助学生整理知识、分析问题，教学生怎样使用条件，培养学生思维的有序性，不断揭示基本知识的生成性，使我们的课堂更生动，使我们的教学更有价值.

本文仅是自己的一点思考，不到之处恳请批评指正.