奶站最佳位置问题及解决策略
2015-05-30李云虎
李云虎
[摘要]主要叙述了在解决平面几何中“线段距离之和最短”这类问题时,经常利用作对称点的方法把折线问题转化为线段的问题来处理.
[关键词]距离之和最短对称
[中图分类号]G633.6[文献标识码]A[文章编号]16746058(2015)110048
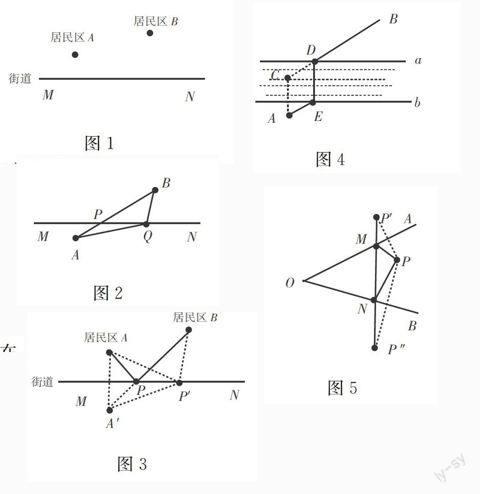
问题:(新课标北师大版《数学》七年级下册第123页的“问题解决”第5题)如图1所示,要在街道MN旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
图1分析:这是一个典型的最短路线问题,难度较大,学生感到困难的地方有两处:一是第一次遇到证明某条线段(或线段的和)最短,无从下手;二是证明中要另选一点,学生一般想不到,不会用.要正确解答这个题目,首先必须知道有关线段大小关系的定理(或公理):两点之间线段最短,或三角形中任意两边之和大于第三边.实际上,两点之间线段最短与三角形中任意两边之和大于第三边是一个道理;其次必须明确证明“最大”“最小”这类问题,常常另选一个量,通过与证明的那个“最大”“最小”量进行比较来证明.
图2我们知道,如果点A、B在直线MN的两侧(如图2),连接AB与直线MN交于P点,那么PA+PB的值最小.这是因为:若在直线MN上任取一点Q(与点P不重合),由“三角形中任意两边之和大于第三边”很容易得到:QA+QB>AB,而AB=PA+PB,所以PA+PB的值最小.
根据上述这一结论,我们可以利用转化的思想把两点在“同侧”转化为两点在“异侧”,问题即可迎刃而解.
图3如图3,要在直线MN上求一点P,使得PA+PB最小.可以把PA+PB连成一条线段,因为两点之间线段最短.为此 ,可作点A(或B)的对称点A′(或B′),连接BA′(或AB′)交直线MN于点P,则点P就是牛奶站所处的位置.
理由:在直线MN上另取一点P′(与点P不重合),连接AP、AP′、A′P′、BP′,因为直线MN是点A、A′的对称轴,点P、P′在对称轴上,所以PA=PA′,AP′=A′P′,所以PA+PB=PA′+PB=A′B.在△A′P′B′中,因为A′B 由此可见,在解决这类问题时,可利用作对称点把折线问题转化为线段的问题来解决.我们把这类求最近路程的问题称为最短路线问题.最短路线问题在生产、科研和日常生活中有着十分重要的应用,下面通过例题来说明. 【例1】A、B两个村庄,中间隔了一条小河,现要在小河上架一座小桥,使它垂直于河岸.请在河的两岸选择合适的建桥地点,使A、B两个村子之间的路程最短. 分析:因为桥垂直于河岸,所以最短路线必然是一条折线,直接找出这条折线很困难.于是想到要把折线化为直线,由于桥的长度相当于河宽,而河宽是定值,所以桥长也是定值.因此,从A点作河岸的垂线,并在垂线上取AC等于河宽,就相当于把河宽预先扣除,连接BC,交河岸a于D点,就在D处建桥即可. 图4解:如图4,过A点作河岸的垂线,在垂线上截取AC的长等于河宽,连接BC,交河岸a于D点,作DE垂直于河岸,交河岸b于E点,D、E两点就是使两村路程最短的建桥地点.即最短路程为AE+ED+DB. 图5【例3】如图5,一个牧羊人早上赶着羊群,从家P地出发去草地OA吃草,回来时再到河边OB饮水,然后再回到P处,请问牧羊人怎样走才能使放牧的路线最短? 解:分别作P关于OA、OB的对称点P′、P″,连接P′P″,分别交OA、OB于M、N两点,则P→M→N→P是最短路线,即最短路程为PM+MN+NP. 根据对称性可知,最短路程就等于线段P′P″的长度. [参考文献] [1]马复.义务教育课程标准实验教科书《数学》(七年级下册)[M].北京:北京师范大学出版社,2013. [2]夏新桥.读打油诗,解数学题[J].数学通讯,2003(23). (责任编辑钟伟芳)