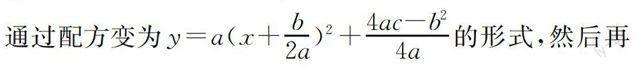求函数最值问题的常用方法例析

陶飞

[摘要]求函数最值问题的方法很多，在练习和习题过程中，学生要学会根据不同的题型，选择合适的解题方法.主要结合具体的数学题型，介绍几种常用的函数最值求解方法.

[关键词]高中数学数学思想函数最值问题常用方法

[中图分类号]G633.6[文献标识码]A[文章编号]16746058（2015）110044

高中数学教学过程中，教师要重视数学思想、数学方法的传授.特别是解题教学，要引导学生学会审题和解题.数学的解题技巧直接影响解题的速度和质量，数学方法是极具教育价值的宝库，是重要的教学资源.教师应最大化地发挥数学解题方法和数学思想的导向与引领作用，通过练习巩固和拓展提高学生的解题能力.

求函数最值问题是高中数学函数教学内容中的重点和难点，其涉及的知识内容很多，解题方法也具有很强的技巧性，既要求学生有扎实的基本功，又要求学生有良好的数学思维能力.从近几年的高考试题和学生的做题情况来看，函数最值问题难度大、要求高，学生很容易失分.现本文结合具体的数学题型，介绍如下几种常用的函数最值求解方法.

一、配方法

配方法是求函数最值较为常见的一种方法，主要应用于二次函数或者可以转化为二次函数类型的函数最值问题求解，其常见形式为将二次函数y=ax2+bx+c通过配方变为y=a（x+b2a）2+4ac-b24a的形式，然后再结合定义域的具体取值范围来求解函数最值.

【例1】求函数y=x2-4x+1，x∈[1，4]的最值.

解：y=x2-4x+1=（x-2）2-3.

当x=2时，y有最小值为-3；

当x=4时，y有最大值为1.

分析：如果函数为二次函数，学生在用配方法求其最值时，需要注意定义域的取值范围和对称轴之间的关系，其主要分为两类：对称轴在定义域取值范围内和对称轴在定义域取值范围外.如果对称轴在定义域取值范围内，则顶点处的函数值为其最值之一，另一最值在其端点处；如果对称轴在其定义域之外，则其最值都在其端点处.同时，如果函数可以转化为二次函数形式，在求其最值时，学生需要注意其隐含的条件与对称轴的关系，如三角函数的取值范围、对数函数的限制等.

思维的方向和敏捷度直接决定思维的质量.在高中数学教学中，教师应联系教学内容，引导学生学会思维.在运用配方法求函数最值问题的教学中，教会学生利用已知的条件去分析题目的要求，根据条件去寻找方法.

而当切线的斜率不存在时，x=±a2b2a2+b2与x2a2+y2b2=1的两个交点为（a2b2a2+b2，±a2b2a2+b2）或（-a2b2a2+b2，±a2b2a2+b2）满足OA⊥OB.

我们可以得到下面的推论.

三、推论

推论1：椭圆x2a2+y2b2=1中，存在圆x2+y2=a2b2a2+b2的任意切线交于椭圆两点A、B，使得OA⊥OB.

我们进一步讨论：在双曲线中是否也存在以坐标原点为圆心的圆使得切线交于曲线两点A，B，并使得.

设x2a2-y2b2=1

y=kx+m，得

b2x2-a2（k2x2+2kxm+m2）=a2b2，整理为（b2-a2k2）x2-2a2kxm-a2m2-a2b2=0.

由韦达定理得

x1+x2=2a2kmb2-a2k2

x1x2=-a2m2+a2b2b2-a2k2，

由y=kx+m得

y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2=（-a2m2-a2b2）k2b2-a2k2+2a2k2m2b2-a2k2+m2，即y1y2=b2m2-a2b2k2b2-a2k2.

要使OA⊥OB，必须满足

x1x1+y1y2=-a2m2-a2b2b2-a2k2+b2m2-a2b2k2b2-a2k2=（b2-a2）m2-a2b2-a2b2k2b2+a2k2=0，即（b2-a2）m2-a2b2-a2b2k2=0，k2=b2-a2a2b2-1.

因为直线y=kx+m为圆心在原点的圆的一条切线，所以圆的半径为r=|m|1+k2，得r2=m21+k2=|m21+b2-a2a2b2-1|=|a2b2a2-b2|.而切线不存在斜率时，也满足OA⊥OB.

推论2：双曲线x2a2-y2b2=1中，存在圆x2+y2=|a2b2a2-b2|的任意切线交于椭圆两点A、B，使得OA⊥OB.

我们不妨设想，当椭圆中a=b时则转化为圆，在圆中，此时.

于是我们得到推论3

推论3：两个同心圆，小圆的半径为大圆半径的时，小圆的任意切线交于大圆的两点，且两点分别与圆心的连线相垂直.

根据，这时，圆上的两点AB与圆心构成的面积最大.

当圆心在平面任意一点，圆也具有以上性质.

（责任编辑钟伟芳）