社交网络话题传播模型剪枝策略研究

殷泽龙 张炜

摘 要：在进行社交网络话题传播时，随着数据量的不断增大，传播模型在进行传播模拟时所花销的时间更多，程序运行所占用存储空间也更大。然而，在实际的话题传播过程中，大多数话题集中在某些关键节点上，且相当一部分节点对话题的传播没有太大的影响。因此，如果在进行话题传播时，我们能够剪掉社交网络中的某些传播节点，这不仅能够减少程序的运行时间，而且能够降低数据所占用的存储空间。针对上述问题，我们设计了两种新颖的图剪枝算法来减少社交网络中的节点数量。本文所提出的两种算法是将推荐系统的思想引入到社交网络传播模型的剪枝策略研究中，具有一定的新颖性。通过实验分析，我们对比分析了不同剪枝策略对传播模型的效果，所占空间，运行时间以及图的健壮性的影响。

关键词：社交网络；剪枝策略；传播模型；话题

中图分类号：TP391.41 文献标识号：A

The Research on Pruning Strategies Topic Propagation Model of Social Network

YIN Zelong， TANG Xianglong

（School of Computer Science and Technology， Harbin Institute of Technology， Harbin 150001， China）

Abstract： With the spreading of topics in the social network， topic models would spent more time and more storage space with the increase of the size of data. However， most topics focus on some key nodes and parts of nodes have no significant effect on topic propagation in the real process of topic propagation. If we could reasonably cut some nodes in the social network during the spread of topics， the runtime of the program and the storage space both would be reduced. To solve the above problem， the paper designs two novel graph pruning algorithm to reduce the number of nodes in the social network. The two algorithms presented in this paper introduced the thought of recommend system into the research on pruning strategy of topic propagation models and have a certain novelty. With the analysis and comparison， the paper analyzes the impact of different pruning strategies of propagation model on the effectiveness， the space， running time and the robustness of the graph.

Keywords： Social Network； Pruning Strategy； Propagation Model； Topic

0 引 言

剪枝是一种机器学习技术，通过移除树的某些节点来减少决策树的大小，其中这些节点对分类实例拥有很小的影响因子[1-2]。剪枝不仅能够减小算法的复杂性，同时还能够提高算法的预测准确性。

在决策树算法中，一个重要的问题就是优化最终树的规模。如果树的规模过大，就会存在训练数据集过度拟合而新样本概括不准确的问题；树的规模过小也会无法把握样本空间重要的信息结构。同时，也很难分析出算法何时应该停止，因为此时仍无法判断新加入的节点能否动态地减少错误，这个问题被称为视界效应。一个一般化的策略是让树自然生长直到停止为止，再使用剪枝策略去移除那些没有重要作用的节点。

在本文中，研究拟将将剪枝技术运用到社交网络话题传播模型中。在进行社交网络话题传播时，话题在不同的用户之间相互传播，这些用户则形成了社交网络关系图[3]。当随着时间不断向前推移，社交网络关系图变得更加复杂，则话题传播模型在这样的社交关系图上模拟将会花费更多的时间和空间。为了节省空间和时间开销，本文提出并设计了两种新颖的图剪枝策略来减少社交网络图中的节点数量。文中的算法是将推荐系统的思想引入到社交网络传播模型剪枝策略中，具有一定的新颖性。在本文实验部分，则将本文提出的算法同随机剪枝策略[4]和基于度的剪枝策略[5]进行比较分析，结果表明本文的算法在剪枝效果上具有明确显著的优越性。

1 问题定义

该小节介绍了相关概念和符号以及社交网络话题传播模型剪枝问题的定义。在此假设给定一个社交网络关系图 ， 是社交网络关系图中用户的集合， 是社交网络关系图中用户和用户关系的集合。同时假设以关键词 作为用户讨论的话题，且在社交网络关系图 中存在的话题集合为 ，由于话题在社交网络中是分布在不同的用户 上，因此 和 之间存在二元映射关系，如图1所示。

图1 话题与用户的映射关系图

Fig.1 Mapping relationship between topics and users

一个用户可以包含多个话题，一个话题也可能对应多个用户。同时话题对于不同用户，其权重也是不同的，因此上假设关键词 对于用户 的权重为 。根据上述定义，可以抽象出本文的研究问题：已知社交网络关系图 和话题集合 ，求出 。为了解决上述问题，本文提出了两种新颖的图剪枝算法，根据 和话题集合 提供的信息，结合图剪枝算法来获取 。下面将介绍本文所研究的社交网络话题模型的剪枝策略。

2 剪枝策略算法研究

本节介绍了两种社交网络话题模型的剪枝策略，基于话题权重和基于用户兴趣相似性的剪枝策略。总而言之，这两种算法均是将推荐系统的思想引入图剪枝策略中。

2.1 基于用户话题权重的剪枝策略

基于用户话题权重的剪枝策略与基于用户兴趣相似度剪枝策略类似，都是利用了话题与用户之间的关系。不同之处是后者计算与用户具有共同兴趣用户广泛度，前者是计算拥有话题的广泛度。在传播模型中，如果多个话题出现在某个用户上，则在一定程度上可以说明话题在传播过程中频繁地经过该用户，因此这样的用户可以被看作关键用户。基于上述的原因，研发设计了一种基于用户话题权重的剪枝策略算法。

假设社交网络关系图为 以及话题集合为 ，每一个话题 被一个或者几个用户所拥有，则假设拥有话题 的用户集合为 ，用户 拥有话题 的权重为 。首先，对每一个话题 的用户集合 按照用户 拥有该话题的权重 进行排序，如图2所示。

图 2 基于话题权重的剪枝步骤1

Fig.2 Topic weight pruning step 1

然后，将每个话题的用户按照从小到大的顺序进行编码，如图3所示。

图 3 基于话题权重的剪枝步骤2

Fig.3 Topic weight pruning step 2

最后，循环遍历每一个 来统计每一个 的话题权重总和，并排序，如图4所示。

图 4 基于话题权重的剪枝步骤3

Fig.4 Topic weight pruning step 3

2.2 基于用户兴趣相似度的剪枝策略

在本节中，给出了话题集合 与用户集合 存在映射关系，即同一个用户可以拥有多个话题，同一个话题可以被多个用户拥有，因此即以用户拥有的话题相似性来表示用户的兴趣相似性。在以上研究中，已经阐述到用户的兴趣相似度对话题转移概率是有影响的，当用户间兴趣相似度越大，则话题更有可能在同群用户之间经常传播。如果某个用户与很多用户均具有颇高的兴趣相似度，则这样的用户就是话题传播过程中的关键用户而应该得到保留。假设用户 的话题集合分别为 和 ，则采用cosine-index[6]来衡量兴趣相似度，即：

（1）

由公式（1）可知，可以计算出 的 。下面将以4个用户（ ）为例来说明该算法步骤。当计算出所有用户之间的兴趣相似度后，就可以得到如下所示的矩阵图：

图 5 基于用户兴趣相似性的剪枝步骤1

Fig.5 Interest similarity pruning step 1

如图5所示，该图的前半部分表示用户兴趣相似度的矩阵图，后半部分即将每一个用户与之关联的用户兴趣相似度进行排序。而后再对排序后的矩阵进行归一化处理，如图6所示。

图 6 基于用户兴趣相似性的剪枝步骤2

Fig.6 Interest similarity pruning step 2

最后，则将归一化的矩阵中每一个用户的兴趣相似度进行统计，并排序得到综合结果。具体如图7所示。

图 7 基于用户兴趣相似性的剪枝步骤3

Fig.7 Interest similarity pruning step 3

用户最终得到的权值越大，就说明用户和周围用户有着更为广泛的兴趣相似度，反之亦然。

3 实验结果与结论分析

本节主要介绍上述几种剪枝策略的实验设计原理以及实验结果。实验中采用真实的微博数据集来构建社交网络关系图和相关话题的提取，并运用上述几种剪枝策略来对社交网络关系图进行剪枝，完成后则将传播模型的算法在剪枝后的社交网络关系图上进行传播模拟，从而比较不同剪枝策略下传播模型的预测效果。

3.1 数据集

本文采用的是微博数据集，抽取的是在某一时间粒度下的数据集来构建社交网络关系图以及话题的抽取，实验数据及环境配置如表1所示。

表 1 实验数据及环境配置

Tab.1 The experimental data and environment configuration

名称 参数

实验数据 User（节点）

Connection（边）

Topic（话题） 11589

72395

107

机器配置 8G RAM，3.40GHZ Core i7 处理器

编程语言 C++

分析工具 Matlab2010，Excel

数据库 Mysql

3.2 实验设计

本节从新浪微博数据中选取了11 589个节点以及106 198条边构成一个社交网络关系图，并从中抽取107个话题。首先是将不同的剪枝策略对社交网络关系图进行剪枝，然后用传播模型算法分别在不同的剪枝后的关系图上模拟话题传播，比较不同剪枝策略下的预测效果和运行时间。同时，对于每一种剪枝策略，均将会构建实验并据此分析不同剪枝程度对传播模型话题预测效果的影响。

3.3 实验效果评估

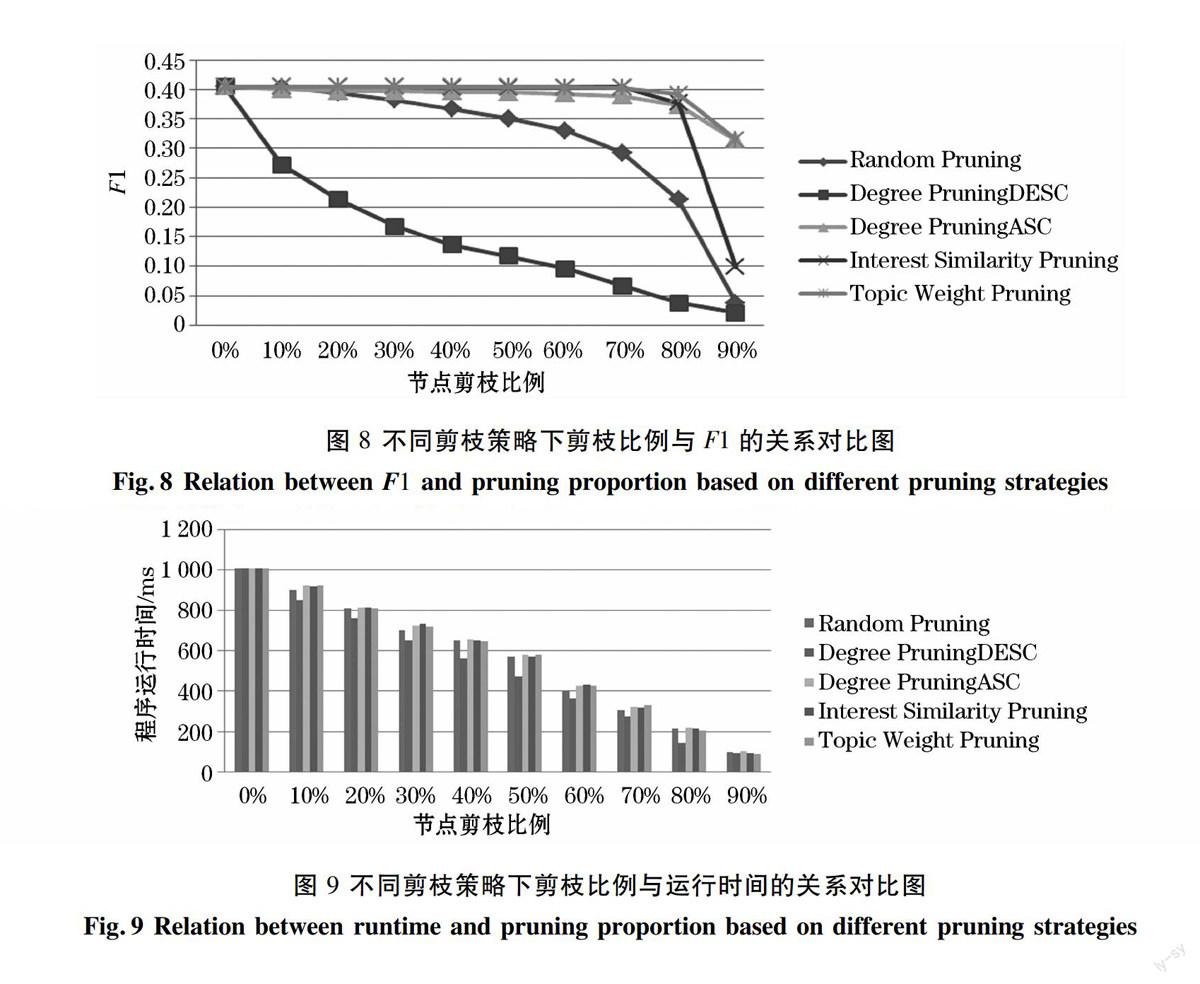
图8是将准确率和召回率进行结合所得到关于不同剪枝策略对于剪枝比例同传播模型F1值关系的曲线图。从图中可以看出，Degree PruningASC 的F1变化最快也是最低，主要是因为按照节点度数从大到小的顺序进行剪枝，首先就会剪掉一些关键节点。其次是Random Pruning，然后是Degree PruningDESC。上述三种剪枝方式从某种程度可以反映出节点的度数同节点的影响力之间的正相关性。Interest Similarity Pruning和 Topic Weight Pruning在随着剪枝比例增大时，前期对传播模型的准确率并没有太多的影响。到后期时二者的F1值都会发生下降，但Interest Similarity Pruning的F1值会出现陡降，因为当剪枝比例越大时，通过Interest Similarity Pruning所剪掉的节点才是正真意义上的关键传播节点，因此将会导致话题传播严重受阻，F1急速下降。

图 8 不同剪枝策略下剪枝比例与F1的关系对比图

Fig.8 Relation between F1 and pruning proportion based on different pruning strategies

图9 展示了不同剪枝策略下，剪枝比例同程序运行时间的关系图。整体上看，随着剪枝比例增大，所用的时间呈线性下降。Degree PruningDESC的程序运行时间低于其他剪枝策略，因为这具体是按照节点度数从大往小进行剪枝，将容易破坏图的连通性，致使信息传播受阻。其次是Random Pruning。利用Interest Similarity Pruning，Degree PruningASC 以及Topic Weight Pruning三种剪枝策略剪枝后，传播模型的运行时间将十分相近，这在某种程度来说如上三种剪枝策略都能够保证社交网络中图的连通性。

图 9 不同剪枝策略下剪枝比例与运行时间的关系对比图

Fig.9 Relation between runtime and pruning proportion based on different pruning strategies

4 结束语

本文主要是介绍并研究社交网络传播模型剪枝策略。因为在进行社交网络话题传播的过程中，数据量会不断地增大，传播模型在进行传播模拟时所花销的时间必将增多，程序运行所占用的空间也会不断加大，所以本文提出了几种社交网络传播模型的剪枝策略来对社交网络进行削减，保证在不降低传播模型预测效果的情况下，能够减少传播模型所花销的时间和空间。首先，本文给出了社交网络话题传播模型剪枝策略研究的相关概念和问题定义，主要包括图的定义，话题定义以及研究的问题描述。其次，本文给出了两种新颖的剪枝策略，包括基于用户兴趣相似性的剪枝策略和基于用户话题权重的剪枝策略。最后，本文又给出了上述几种算法的实验分析结果，主要从时间的运行效率，所包含节点比例以及传播模型的预测效果来进行对比和分析。实验结果表明，按节点度大的顺序进行剪枝的效果最差，但是模型的运行时间最短；其次是随机剪枝，效果和运行时间居中；基于用户话题权重的剪枝策略，预测效果表现最好，同时剪枝策略设计并不复杂。

参考文献：

[1] HARABOR D， GRASTIEN A. Online graph pruning for pathfinding on grid maps[C]//Association for the Advancement of Artificial Intelligence ，San Francisco， CA， USA：AAAI， 2011.

[2] KRETZSCHMAR H， STACHNISS C， GRISETTI G. Efficient information-theoretic graph pruning for graph-based SLAM with laser range finders[C]//Intelligent Robots and Systems（IROS），San Francisco， CA ：IEEE/RSJ，2011 ：865-871.

[3] DENG H， HAN J， ZHAO B， et al. Probabilistic topic models with biased propagation on heterogeneous information networks[C]// KDD11， New York， NY， USA：ACM， 2011：1271-1279

[4] GOYAL A， BONCHI F， LAKSHMANAN L V S. A Data-Based Approach to Social Influence Maximization[J]. VLDB 2012， 2012，5（1）：73-84

[5] KWAI D， PARHAMI B. A Class of Fixed-Degree Cayley-Graph Interconnection Networks Derived by Pruning k-ary n-cubes[C]// ICPP97 Proceedings of the international Conference on Parallel Processing，Bloomington， IL：IEEE， 1997：92-95.

[6] JOSIFOVSKI V. Comparison of similarity search algorithm over inverted indexes[R]. Stanford：Project for MS&E239 Autum 2010， 2010.