高职教育中定积分应用的教学研究高职教育中定积分应用的教学研究

郭小林

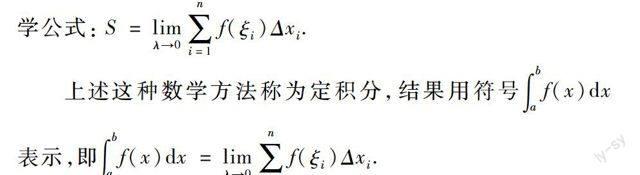
【摘要】高等数学是高职教育中一门重要的基础学科，定积分在其他学科中应用非常多.这客观上要求讲授定积分不仅要教会学生定积分的基础计算，还要教会学生能熟练应用定积分处理相应的社会问题.本文从定积分概念出发，重点讲述微元法的认识和使用，最后举例说明定积分应用和使用.

【关键词】定积分；微元法；应用；扩展

高职的培养目标是在某一工作岗位上有技术专长的操作能手，侧重于专业技能的培养，高职高专数学教学是培养高等技术应用型人才的重要途径.积分理论是高等数学中的重点部分，而整个积分理论是用于解决实际问题使用的重要思想和方法.故此，高职数学教育中要特别注重积分的教学研究和方法，更要使得高职学生能熟练掌握积分的应用.积分的应用主要表现在定积分的应用.

1.定积分应用教学的难点

在传统数学教学模式下，会造成重理论、轻应用的教学模式，会给学生造成一定的误解，定积分的计算方法学得很扎实，而定积分应用仅限于书本上的面积、体积等例题的应用.造成这些问题的原因归结于：对定积分概念掌握不足，对微元法思想掌握不足，对定积分的应用范围掌握不足.因此，高职数学教学过程中必须加强教学研究，加强数学应用技能的教学研究.

2.定积分应用的教学要点

要使学生深刻掌握定积分，并能正确应用定积分解决实际问题，在教学要点中要努力做到以下方面：

第一，厘清定积分的概念

曲边梯形的面积是作为定积分概念引入案例.此案例非常重要，一个看似无法求解面积的图形，居然可以用一套特殊数学方法就求出面积.需要让学生掌握求面积的四个步骤：分割——近似——求和——求极限，得到求面积的数学公式：

S=limλ→0∑ni=1f（ξi）Δxi.

上述这种数学方法称为定积分，结果用符号∫baf（x）dx表示，即

∫baf（x）dx=limλ→0∑ni=1f（ξi）Δxi.

这样可以使得学生清楚认识，定积分是基于处理实际问题产生的，现实世界中还有许多类似问题，都可以用定积分的方法求解.

第二，微元法扩展了定积分应用

微元法是定积分应用部分的教学重点，也是对定积分概念的重塑，可以使定积分走出几何面积的束缚，向其他应用体积长度等方面扩展.同样需要让学生熟练掌握微元法的步骤：分割——近似——求定积分.微元法的精髓在于：不仅可以分割面积，还可以分割体积、长度等等，被分割的变量用微分d表示，被分割的部分看作一个规则的图形近似计算，最后把近似值在整个区间上进行积分.

此时，∫baf（x）dx中f（x）不仅仅是指曲边梯形的高，f（x）dx可以表示任何一种被分割体的近似计算.

第三，定积分适用于一切变化过程求总量

用微元法扩展定积分应用之后，定积分应用的思维就已经被打开了.可以总结出：凡是不规则的变化过程，需要求总变化量，均可按照微元法应用定积分来解决问题.在自然科学、社会科学和工作生活的计算中，规则的变化几乎不存在，更多的是不规则的变化，要准确求出其变化总量，定积分是最合适的科学计算工具.

3.定积分的应用案例

估计某医院在某时间内的就医人数.

一家新的乡村精神病诊所刚开张，对同类门诊部的统计表明，总有一部分病人第一次来过之后还要来此治疗.如果现在有A个病人第一次来就诊，则t个月后，这些病人中还有A·f（t）个病人还在此治疗，这里f（t）=e-t/20.现在这个诊所最开始接受了300人治疗，并且计划从现在开始每月接受10名新病人.试估计从现在开始15个月后，在此诊所接受治疗的病人有多少？

既然f（15）是15个月后还要来此诊所就诊的病人人数的比例系数，那么在开张时接受的300个病人中15个月后还要再次就诊的人数为P0=300f（15）.

为了计算从现在开始的15个月内新接受的病人在15个月后还在此就诊的人数，根据微元法，将月份0，15分成若干个小区间，取一个小区间作为微元，时间长度为dt，微元近似看作就诊人员是均匀地到来.由于每月接受10人，则微元区间内到来的人数是10dt，在15-t月后还有10dt·f（15-t）人再次就诊.这15个月中就诊的病人在15个月后再次就诊的数量为P1=∫15010f（15-t）dt.

那么总的就诊人数为P=P0+P1=300f（15）+∫15010f（15-t）dt，将f（t）=e-t/20代入可得：P=300e-3/4+10e-3/4∫150et/20dt=247.24（人），因此15个月后，这个诊所将要接待247名左右的病人.

4.总结

高职教育中的数学教育，教学目的在于把数学作为一种工具来学习，并且使学生学习之后能够正确地应用.本文在教学要点的三个要点中，逐步把学生带入定积分的应用世界，能更深刻地认识和领会定积分，能在现实经济社会中遇到变化的情况及时应用定积分.最后通过一个具体的案例运算，详尽展示了定积分的应用过程.