基于小波多分辨率分析的图像边缘检测研究
2015-05-30刘小豫聂维魏浩
刘小豫 聂维 魏浩
摘 要:本文就图像边缘检测的多分辨率分析模型和小波变换多分辨率边缘检测方法进行了分析研究,对基于小波分析的图像边缘检测研究现状进行了分析和总结。明确了研究方向和重点主要集中在小波基的构造和选取,阈值的选取,小波分解的尺度选取,以及小波分析方法和其他方法的结合使用。
关键词:边缘检测;小波变换;多分辨率分析
中图分类号:TP391 文献标识码:A
1 引言(Introduction)
图像边缘是一种重要的视觉信息,是图像最主要的特征之一,它包含了用于识别的有用信息,为人们描述或识别目标以及解释图像提供了一个重要的特征参数[1]。图像边缘就是图像的轮廓,图像信号的突变点、不规则结构和不平稳现象处会产生图像的边缘。使用不同的边缘检测算法,在图像中检测图像像素点的灰度,在给定模板区域上对像素点进行计算,分析灰度是否连续,从而确定边缘在图像中的位置。边缘检测是图像分析与识别中最基础、最重要的内容之一,也是实现图像分割、特征(纹理特征和形状特征)提取和图像理解的基础。
2 多分辨率分析技术(Multi-resolution analysis
technique)
图像多分辨率分解是进行图像多分辨率处理与分析的核心,他是从人类视觉系统研究、心理学研究中发展起来的。20世纪70年代末期、80年代初期,出现了图像多分辨率分析的算法和方法,多分辨率金字塔分解方法由Burt提出,这是当时最为经典的方法,该方法的特点就是简单。多分辨率金字塔分解方法一种是把图像分解成一组高斯金字塔图像之和,另一种是表示成一组Laplacian金字塔图像之和,分解开的图像在不同分辨率下所表示的信号细节具有相关性[2]。
3 图像多分辨率分析模型及其应用意义(Image
multi-resolution analysis model and its
application)
可以借助于摄像机的镜头来理解尺度的概念,由远及近地使摄像机镜头逼近目标,就类似于尺度由大到小的变化。通过镜头远距离观察目标,容易看到的是事物的轮廓样貌,这种情况类似于在大尺度空间里观察图像。当镜头逐渐接近观察目标,才能观察到事物的细节信息,这种情况类似于在小尺度空间里观察图像。大尺度下图像的分辨率低,小尺度下图像的分辨率高。多分辨率分析的思想就是大尺度下确定轮廓信息,逐步使尺度变小获取细节信息。
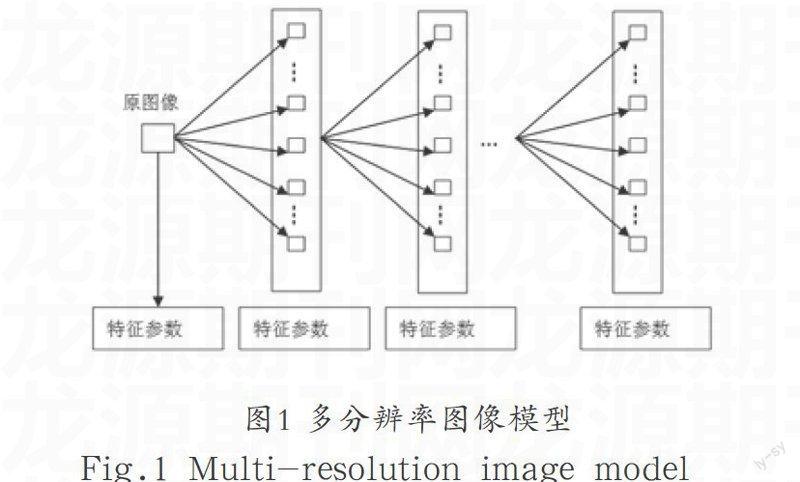
多分辨率图像分析过程就是图像的分解过程,该分解过程就是把图像分解为多个层次来表示。在检测图像边缘时,先在低分辨率下获取图像的轮廓信息,在较高分辨率下获取图像的细节信息,就是在确定图像大致概貌的基础上再不断分析细节部分,逐步添加轮廓的精确边缘。在低分辨率下图像边缘的表征值少,就是确定边缘的大体位置和形状,这部分处理起来比较快。而在高分辨率下图像边缘的细节信息和精确位置需要较多的表征值,但是可以由已知的低分辨率下获取到的边缘轮廓指导高分辨率下边缘细节信息及精确位置的分析,也可以减少运算的时间。普通的多分辨率图像分析模型如图1所示。能够进行在微观和宏观的尺度下的图像分析。多分辨率图像分析方法把传统的在空间域和频率域互相制约的分析方法进行了折中。
图1 多分辨率图像模型
Fig.1 Multi-resolution image model
4 小波变换多分辨率边缘检测(Wavelet transform
multi-resolution edge detection)
小波分析是从时频分析、多分辨率分析研究中发展起来的。傅立叶变换系,即三角函数系在频域上能够完全局部化,但在时间域上不能体现局部性。Haar变换基能够在时间域上完全局部化,而在频率域的局部性体现较差。小波变换在时域和频域上都能表征信号的局部特征,其窗口形状可改变但大小固定不变,是一种时频局部化分析方法,它的时间窗和频率窗均可改变。低频部分具有比较低的时间分辨率及比较高的频率分辨率,高频部分具有比较低的频率分辨率及比较高的时间分辨率,非常适合在正常信号中探测瞬态反常现象,并展示这种反常成分,因此把小波分析誉为分析信号的显微镜。理论上讲,小波分析完全可以取代傅立叶分析。小波分析在时域和频域上同时具有良好的局部化性质优于傅立叶变换[3]。小波变换在图像处理应用中表现出较多的优点。包括图像信号在分解过程中不会产生任何信息的损失,不同分辨率下图像的轮廓信息和细节信息均容易获取;Mallat快速算法为小波变换应用提供了必要手段。
多分辨率图像分析由一组子空间和尺度函数组成。构造多分辨率分析的方法有两种,一种方法是构造一组子空间序列,然后需要找一个尺度函数,这种方法构造尺度空间容易,但找尺度函数很困难;另一种方法是构造一个尺度函数,由这个尺度函数来定义尺度空间,这种方法容易些,目前的绝大多数小波是按此方法构造的。由多分辨率分析出发可以构造小波,这样的小波函数称为对应于多分辨率分析的小波。由多分辨率分析构造的小波只是小波函数全体集合中的一部分。小波变换多分辨率边缘检测,是先构造一个尺度函数,再利用尺度函数把图像分解为多个尺度空间,在不同尺度空间上进行边缘信息的检测,最后对多尺度空间上边缘信息图像进行重构。
小波变换应用重要的一个方面就是检测信号突变点和根据边缘点重建原始信号。在小波域内小波变换模的极值点、过零点作为信号的突变点。目前基于小波变换图像边缘检测方法很多,可以使用B样条小波、以零点为对称点的对称二进制小波、以零点为反对称点的二进制小波及多进制小波等。目前对小波边缘检测的研究正受到很大的关注,研究方向和重点主要集中在以下方面:小波基的构造和选取,阈值的选取,小波分解的尺度选取以及小波分析方法和其他方法的结合检测。
5 结论(Conclusion)
小波变换因其所具有的多分辨率分析能力和时频局部化能力,利用小波变换进行边缘检测能够有效地与人类视觉特性取得一致,因此,小波多分辨率分析正广泛地应用于图像边缘检测中。
参考文献(References)
[1] 何东健.数字图像处理(第2版)[M].西安:西安电子科技大学出 版社,2008.
[2] 杨在原.有噪图像的小波变换多分辨率分割[D].吉林:吉林大 学,2005:4-6.
[3] 毛安定,等.基于Daubechies小波的图像边缘检测技术[J].工程 图学学报,2012,33(1):63-67.
作者简介:
刘小豫(1978-),女,硕士,讲师.研究领域:图像处理, 信息系统开发.
聂 维(1977-),女,硕士,讲师.研究领域:网络安全,信 息系统开发.
魏 浩(1973-),男,硕士,讲师.研究领域:网络安全,数 据挖掘.