常用状态方程描述二氧化碳PV T关系的比较

2015-05-29刘海力湖南人文科技学院能源与机电工程系湖南娄底417000

化工管理 2015年27期

刘海力(湖南人文科技学院能源与机电工程系，湖南娄底 417000)

CO2的PVT关系测定是《热工基础实验》中的一个典型的验证性实验[1-4]。然而，目前该实验并没有涉及到对状态方程的研究，实验时仅让学生观测CO2临界状态现象，测定CO2在不同温度下的压力与比容，绘出CO2的PV曲线。事实上，要想深入了解压力、温度和比容之间的确切关系，就必须对状态方程进行研究[5]。目前比较常用的状态方程有理想气体状态方程、范德瓦尔方程以及R-K方程。本文尝试利用三个常用状态方程在描述CO2的PVT关系时进行比较，以便能更全面了解每个状态方程的特点，为准确预测不同状态下CO2的PVT关系提供参考。

1 常用的三个状态方程

1.1 理想气体状态方程[6，7]

理想气体是一种经过科学抽象的假象气体模型，其气体分子是一些弹性的、不占有容积的质点，分子相互之间没有作用力。理想气体状态方程，是描述理想气体在处于平衡态时，压强、体积、物质的量、温度间关系的状态方程，其数学表达式为：

式中：P 为压力，Pa；v为比容，m3/kg；Rg质量气体常数，J/(kg·K)；T为温度，K。

刘海力（1979-），男，主要从事能源与动力工程专业的教学研究。

1.2 范德瓦尔方程[6，7]

范德瓦尔考虑到气体分子具有一定的容积，所以在范德瓦尔方程中用分子自由活动的空间(v -b)来取代理想气体状态方程中的容积；此外，考虑到气体分子间引力作用将使作用于器壁的压力减小，用内压力a/v2来修正压力项。其数学表达式为：

式中：a与b是与气体种类有关的正常数，称为范德瓦尔常数。

1.3 R—K方程[6，7]

R—K方程是在范德瓦尔方程的基础上提出来的，通过对内压力项a/v2的修正，使精度有较大提高。其数学表达式为：

2 三个状态方程描述二氧化碳PVT关系的比较

2.1 不同温度下的PV曲线

利用二氧化碳PVT关系测定仪（由上海实博实业有限公司生产，型号：LL574）分别测得26℃、31.1℃及40℃的PV关系曲线，如图1所示。

图1 CO2在不同温度下的PV曲线

2.2 三个状态方程计算结果与实验数据比较

保持比容v不变，利用三个状态方程分别计算CO2在26℃、31.1℃及40℃温度下的压力P，计算结果如图2所示。

图2 不同温度下三个状态方程的计算结果与实验数据比较

从图2可见，温度越高、比容越大，状态方程越能准确描述CO2的PVT关系，计算的结果与实验数据越接近；在三个状态方程中，理想气体状态方程的误差最大，即使在高比容、高温（v=0.00947m3/kg，t=40℃）条件下，误差也达56.18%，范德瓦尔方程在高比容阶段比较准确，而R—K方程最适合描述CO2的PVT关系，计算结果几乎与实验数据重合。

2.3 范德瓦尔方程与R—K方程拟合结果比较

范德瓦尔方程与R—K方程比较适合描述CO2的PVT关系，为了进一步比较两个方程的特点，现利用范德瓦尔方程与R—K方程分别对26℃、31.1℃、40℃下的实验曲线进行拟合，得到图3和表1。

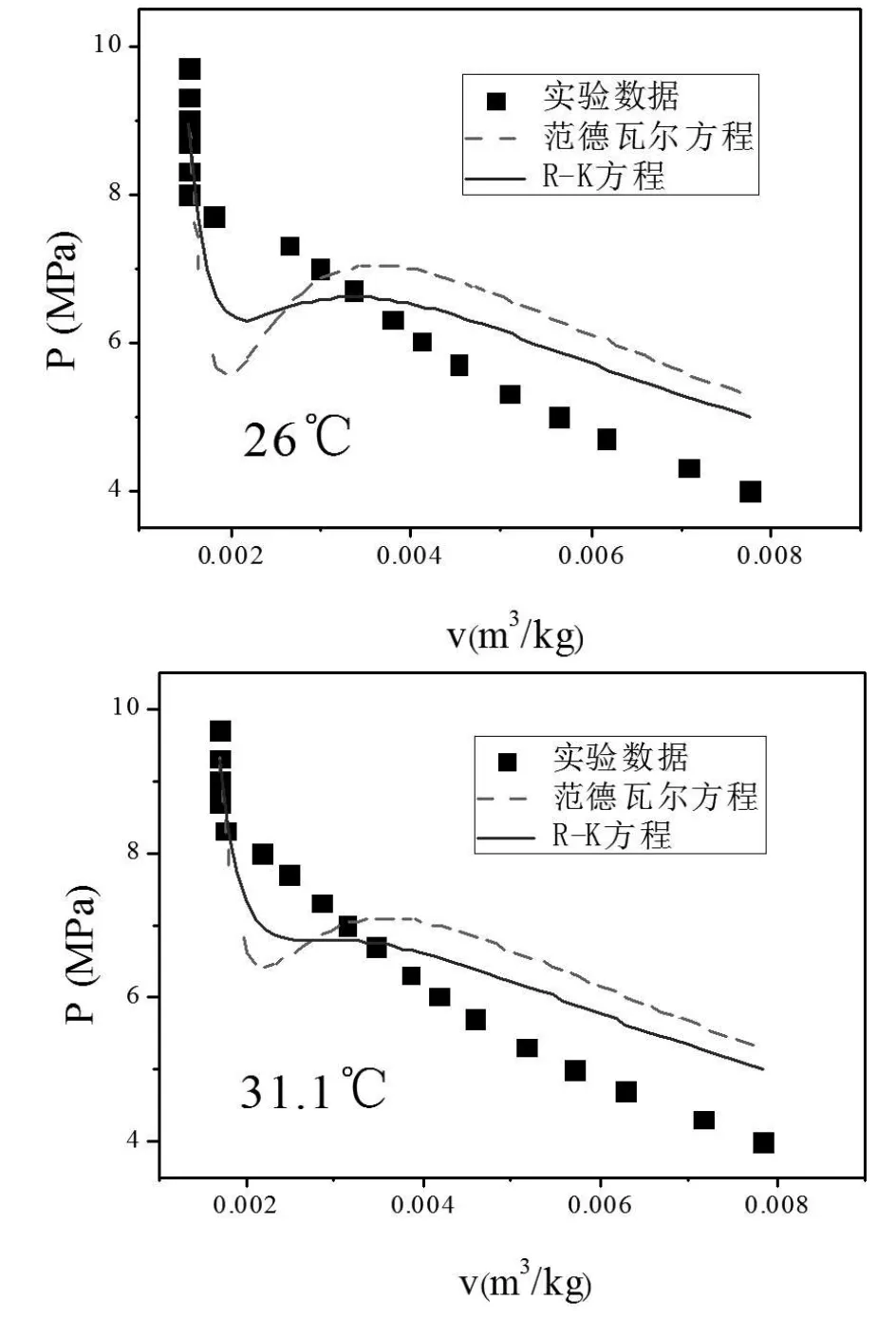
图3 不同温度下范德瓦尔方程与R—K方程拟合曲线

表1 拟合结果表

从图3及表1可看出，温度越高拟合曲线与实验曲线越接近，拟合相关系数越大，说明范德瓦尔方程与R—K方程更加适合描述高温气体，该结论与3.2节一致；在同一温度下，与范德瓦尔方程相比，R—K方程的拟合曲线明显与实验曲线更为接近，拟合相关系数更大，进一步说明R—K方程比范德瓦尔方程更适合描述CO2的PVT关系；2个方程在临界状态附近误差都较大，这是因为2个方程的临界压缩因子都偏大（范德瓦尔方程导出的临界压缩因子Zcr=0.375，R—K方程给出的临界压缩因子Zcr=1/3），而实际CO2的Zcr仅为0.275，因此计算结果与实验数据偏差较大；温度越低，R—K方程的优势更加明显，当温度分别为26℃、31.1℃及40℃时，R—K方程的相关系数分别比范德瓦尔方程分别大了24.32%、20.53%及11.11%。