BWT生成算法在移动平台实现的对比和优化研究

王国政，朱光彦

(中州大学信息工程学，郑州 450044)

一、BWT算法简介以及项目背景

云技术的普及使得越来越多的用户数据从个人终端被转移到了云端。而移动互联网的广泛应用则在很大程度上成就了云端数据与个人用户之间的桥梁。随着移动终端平台的发展，其软硬件能力也得到了大幅度的提升。由此而来的云端数据本地化就成为了移动平台应用的新的发展方向之一。大量的云端数据的本地化涉及到数据的下载、上传和移动平台对离线数据的处理。虽然移动平台有了不错的硬件能力，但是其互联网带宽、硬件空间和内存处理能力仍然存在着很大的局限性。而由此也对该平台上有云端数据本地化需求的应用程序的数据压缩和处理能力提出了很高的要求。

Burrows-Wheeler Transform，也称为BWT变换，就是一种被广泛应用于数据压缩领域的系列算法。其高效的压缩和搜索性能使它的使用领域非常广泛。从一般文本压缩到基于DNA串的高级压缩和搜索操作，都能看到BWT技术的身影。虽然该技术在文本压缩领域有着广泛和深远的影响，其使用范围却受到了运行环境的限制。比如在移动平台(手机、平板电脑)上，该方法对于平台的运算能力和运行时内存的需求就会显得过于繁重。从另一个角度来讲，虽然移动平台在运行时内存和处理速度方面提供具有高束缚性的环境，但也正是这种移动平台对高效的数据压缩类算法有着很大需求。而基于其惊人的压缩比和在保持压缩比的同时提供的高效数据搜索效率的性质，BWT算法在移动平台有着广泛的需求和前景。这种平台束缚性和平台需求的矛盾，使得关于BWT算法是否合适被应用在移动平台之上，就成为了一个非常值得考量的问题。本论文以实际项目为背景，对此问题进行了深入探究。其软件项目基础是一个基于测验的互联网教育类网站“Tenclip”的手机移动平台应用(APP)实现。该网站对其APP处理大量离线的测验数据有着很高的需求，因此产生的对基于文本的数据压缩和搜索的需求，使其理所当然的成为BWT算法实现的优质平台。

二、BWT算法的项目应用

在项目的硬件和软件基础上，BWT作为算法核心支撑着该项目主要功能的实现。BWT算法是现今最高效的压缩算法之一，同时它也对高速的搜索功能有着强有力的支持。正如其英文名称Burrows–Wheeler Transform(变换)所揭示的一样，BWT压缩算法最核心的概念就是对文本T进行的变换。举例来说，如果T=BANANA$，则经过BWT转化后，T就变成了ANNB$AA。通过这种变化，在保证高效(时间复杂度和空间复杂度)的原文全文搜索的基础上，可以进而对变化文本进行高效的压缩。［1］

该移动端应用APP的流程包括:用户首先通过APP测试浏览窗口或者搜索窗口获得需要的Quiz(小测试)。小测试包含单项选择题、多项选择题、填空题和简答题。选定测试之后用户可以直接点击测试题目进入测试进行答题，在答题的过程当中需要网络连接，用户回答完问题后提交自己的答案，APP通过网络对用户的答案进行评估、评分和评奖。或者用户可以选择离线答题模式。APP则会下载用户所选择的测试，以供用户进行离线答题。当网络连接恢复之后，用户的评价体系就会自动完成。

对于每一个测试的数据结合，系统采用BWT算法生成其索引文件(Index Files)，这里应用到的是“BWT生成算法”。因为所有通过网络传输到客户端的文件都要被压缩存储，在此应用的是“BWT压缩算法”。而之后索引文件ID的获得则用到“BWT搜索算法”。

离线数据以两种形式存储在本地。一种被称为“Personal Download个人下载”(简称PD);另一种叫做“Personal Bank个人数据银行”(简称PB)。PB中存储的是网站所有Quiz的离线文本文档，它是用户在下载APP的时候预装的网站当时所有Quiz的快照。PD则包含用户下载的所有的Quiz。他们两者之间可能会有交集。从体积上讲，PD远远小于PB。因为PB的大小一般会超过60M，基于它的BWT创建算法是无法在移动端进行的，所以该部分数据被预装在了APP之中。而PB的大小一般小于1M(在50K左右)，稍后的BWT算法分析中可以看到，即使当PB大小上升到1.5M，普遍的Android移动端还是能胜任其BWT的各种算法过程处理的。

三、BWT算法在移动平台的应用瓶颈

BWT虽然能够同时实现惊人的压缩比和对搜索的高级支持，但是BWT生成算法则可能会很轻易的成为整个算法过程的瓶颈，主要包含以下三点原因:

1.现在普遍认可的 BWT生成算法有两种［2］。一种叫做 Forward Transform Algorithm(简称FT算法)。FT算法基于对原文本的旋转变体(cyclic shifting)的全排列。另一种叫做Native Suffix Array Construction Algorithm(简称NSAC算法)。这种算法首先生成原文本的Suffix Array(后缀数组)，然后通过后缀数组生成BWT文本。NSAC算法的后缀数组又可以通过两种算法生成:原生排序算法或者更复杂的线性排序算法。NSAC算法是比较常用的算法，但是其时间复杂度在最坏的情况下是O(n2)，效率过于低下。

2.要考虑的第二个因素是由于移动系统硬件或者移动操作系统(在这里是Android)导致的在APP在运行的时候的强制的内存限制［3］(试验中为24 M)。

3.第三个阻力是在系统实现的时候可能利用到的Java的本地排序算法。通过Java文档可知，Java的本地排序算法，在一般的排序状况下是能够保证O(nlgn)的时间复杂度的。但是经过系统的实践证明，在具体实现中，尤其是当排序标准不是一般性数字比大小而是自定义排序标准的时候，Java类库提供的本地排序算法并不一定是最好的选择，因为它在时间复杂度和空间复杂度方面都不能提供最佳的运行效率。

下面就通过对三种BWT生成算法的效率以及可以实现的优化两个角度讨论解决以上三个困境的有效途径。

四、问题分析和解决方案

最原始的创建某文本的BWT变体的方式是通过FT算法［4］。该算法的核心思想如表1所示，是对原文本的所有旋转变体进行排序。

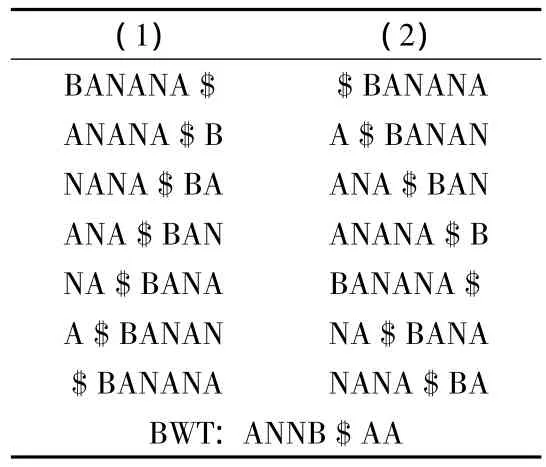
表1

其中表格(1)部分为T的所有旋转变体，(2)即为按照字典序对所有变体的字符串进行的排序。而通过对(2)的最后一个字符的顺序扫描，即可获得T的BWT变体文本:ANNB$AA。

可以看到以上算法的空间复杂度为O(n2)。通过实现一个辅助数组缓存可以实现把空间复杂度降低到O(n)。时间复杂度方面，理论上O(nlgn)的时间复杂度效率是可以实现的，但是一旦我们转化的文本文字来自于英文文本，其最坏时间复杂度O(n2)就变得非常的常见了，因为Java原生排序的算法多是基于各种快速排序(Quick Sort)的变体。

第二种生成BWT变体的算法是通过后缀数组的线性变化实现的。思路很简单，一段文本T的BWT变体即为T的后缀数组的每一个字符的前一个字符构成。如表2所示F为后缀数组，L即为T的BWT变体。

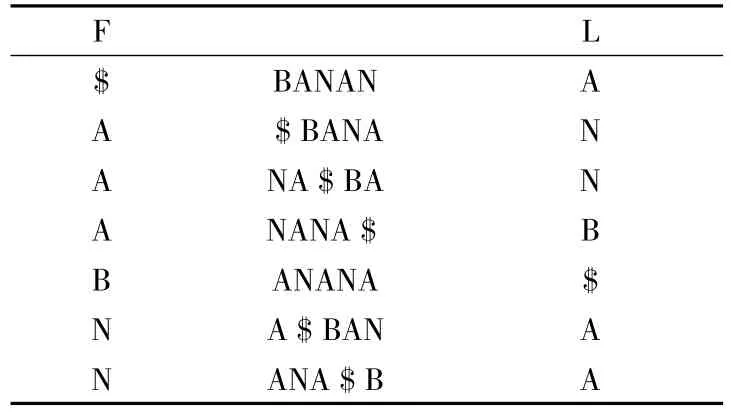
表2

因为该算法通过线性扫描后缀数组实现，它的运行效率也就主要依赖于后缀数组的生成算法的选择。3种主流算法在该项目中进行了比对研究。第一种算法叫做Native Suffix Array(NSA)创建算法，与前文讨论过的FT算法类似，它也是依靠对所有后缀数组的全排序。其时间复杂度基于所选择的排序算法在一般情况下可以控制在O(nlgn)，但是基于不同的原文文本语言，O(n2)的情况也会变得比较常见。

如图1基准测试所示，该算法只适用于对小于100K的文本文档进行处理，对大于100K的原文本文档，消耗的时间超过40秒。如果是大于400K的测试文档，算法所消耗内存超出Android系统的对于单个程序运行的内存限制。在时间复杂度和空间复杂度方面的表现不佳，使得实施更加优质算法成为必要。

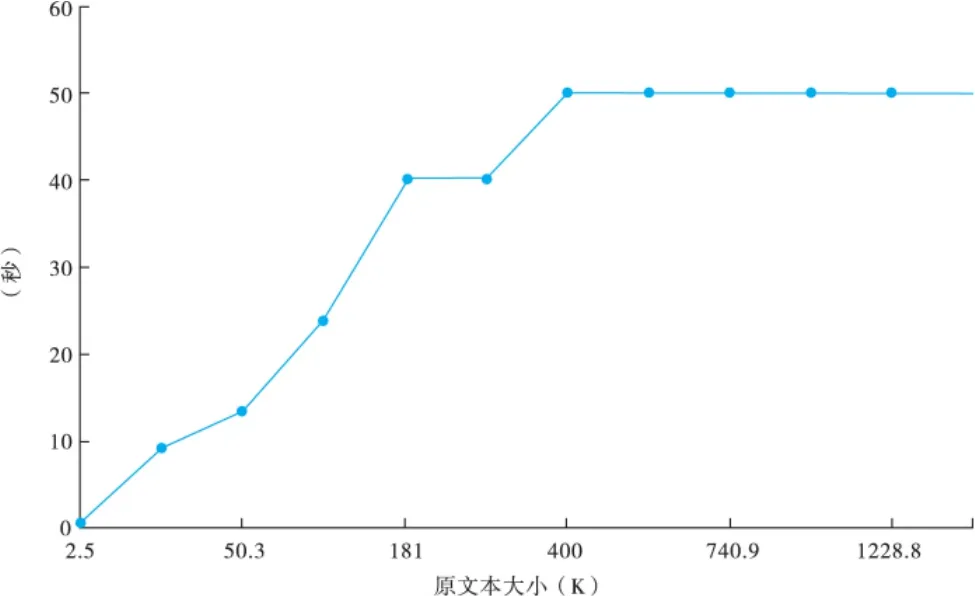
图1 NSA算法的BWT变体生成效率基准测试

第二种和第三种算法的后缀数组的生成算法都是线性的时间复杂度，他们都基于同一种思路:先把原文本部分排序，再用排序的部分对剩余的部分进行全排序。第二种算法被称之为DC3(或者叫做skew)［5］。第三种线性算法叫做 SAIS［6］，它被称为现阶段时间复杂度和空间复杂度效率最高的算法。以下就这两种算法的基准测试效果如图2所示(注:其中蓝色(最左侧)曲线仍为NSA算法;橘黄色(右侧倒数第二条)曲线为Skew算法;灰色(最右侧)线表示的是在对Skew算法进行了轻量级Java实现优化后的表现;紫色(左起第二条)曲线表示SAIS算法)。

可以看到SAIS实际上在SKEW没有超出内存的情况下并没有速度优势。但是在空间使用方面，即使对于超过1.5M的文本文件，SAIS算法也能够保证在不内存溢出的情况下，25秒的时间内完成任务，在移动平台上这种运行效率是相当惊人的。

图2 两种算法基准测试效果

五、结论

经过本项目的比对，在BWT生成算法阶段，不同的算法体现出了对系统不同的要求和效率。总体来讲，由于其在时间复杂度和空间复杂度方面的低效表现，原生排序算法应该被排除在可选的算法行列。如果要处理的文件小于500K，Skew算法应该被给予优先考虑。因为在移动平台硬件和软件系统的限制下，Skew算法表现出了高效的运算效率和空间使用效率。而对于大于500K的数据，更加稳定的SAIX算法应该被采用。虽然在速度上稍逊一筹，其在时间和空间很好的平衡性使得其在更大的数据样本上成为更加合适的选择。通过以上的优化，BWT的生成算法阶段的三个瓶颈就可以被有效克服，使其在移动平台上的高效应用成为现实。

自从Michael Burrows和David Wheeler于1994年发明了BWT算法以来，其高效的压缩比和变形后强大的数据获取以及搜索能力都成为该算法被广泛应用于各个领域的重要原因。尤其是在大量云数据需要本地化的需求面前，其应用前景也变得格外广阔。移动平台的硬件束缚与BWT搜索算法高需求之间的矛盾仍然是需要解决的一个很重要的问题，其解决方案也将成为今后相关研究的核心发展方向。

［1］Donald Adjeroh，Timothy Bell，Amar Mukherjee.The Burrows-Wheeler Transform，Data Compression，Suffix Arrays，and Pattern matching［M］.Berlin:Springer Science Business Media，2008.

［2］Ferragina P，Manzini G.Opportunistic data structures with applications［J］.Proc.41st Annual Symp.on Foundations of Comp.Sci.，2000:390.

［3］孔凡良.Java程序内存泄漏研究［J］.科技广场，2009(9).

［4］Raymond K W，Franky Lam，William M S.Querying and maintaining a compact XML storage［R］.Proceedings of the 16th international conference on World Wide Web，2007.

［5］刘小华，翟有利.灵活的面向字节基于词的压缩搜索算法［EB/OL］.(2013-11-11).［2015-02-07］.http://www.paper.edu.cn/releasepaper/content/201311-193.

［6］Ge Nong，Sen Zhang，Wai Hong Chan.Two Efficient Algorithms for Linear Time Suffix Array Construction，IEEE Transactions on Computers［C］.IEEE computer Society Digital Library，2010.

［7］Kieffer J C，Yang E H，Nelson G J，et al.Universal lossless compression via multilevel pattern matching［J］.IEEE Transactions on Information Theory，2000，46(4):1227-1245.