平面弹性问题的有限元程序设计
2015-05-29任国彪冯美禄
任国彪,冯美禄
(1.郑州大学数学与统计学院,郑州 450052;2.河南省教育技术装备管理中心,郑州 450001)
1 引言
平面弹性问题是工程上经常遇到的问题,用有限元方法解决平面弹性问题具有计算精度高、方法规则简单的特点。但相对于一般的二阶问题和四阶问题标量求解不同,平面问题要求的是一个向量解,另外在解和Locking上也有不同的限制。因此,平面弹性问题求解时比较复杂,作者根据求解该问题时遇到的情况以及相关的一些思路做出阐述。
有限元法发展到今天,已成为工程数值分析的有力工具。特别是在固体力学和结构分析领域内,有限元法取得了巨大的进展,利用它已成功地解决了一大批有重大意义的问题,很多通用程序和专用程序投入了实际应用。同时,有限元法又是仍在快速发展的一个学科领域,它的理论,特别是应用方面的文献经常且大量地出现在各种刊物和文集当中。三十多年来,有限元法的应用已由弹性力学平面问题扩展到空间问题、板壳问题;由静力平衡问题扩展到稳定问题、动力问题和波动问题。分析的对象从弹性材料扩展到塑性、粘弹性、粘塑性和复合材料等;从固体力学扩展到流体力学、传热学等连续介质力学领域。在工程分析中的作用已从分析和校核扩展到优化设计并和计算机辅助设计技术相结合。可以预计,随着现代力学、计算数学和计算机科学技术等学科的发展,有限元法作为一个具有巩固理论基础和广泛应用效力的数值分析工具,必将在国民经济建设和科学技术发展中发挥更大的作用,其自身亦将得到进一步的发展和完善。
有限元法是现代工程设计和科学计算的重要数值方法之一。利用计算机有限元软件对工程问题进行数值计算和分析已成为有限元法中一个必不可少的环节。
2 平面弹性问题的模型

2.1 下面考虑纯位移的平面弹性问题:
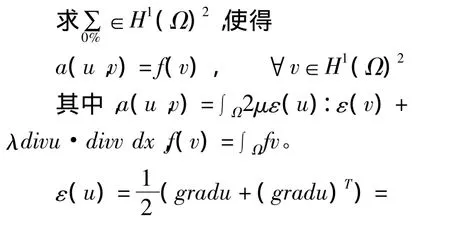

2.2 离散方程
设平面弹性有限元(K,PK,∑K),单元自由度数为en,总体自由度数为MP,有限元空间为Vh,由有限元导出的插值函数为:

2.3 求标准基函数
对于自由度较少的单元,可以直接求解其标准基函数,对于自由度比较复杂的单元,如采用边积分值、外法向导数值、单元积分值,标准基函数比较复杂,手工很难求出。其实,在有限元计算中,标准基函数不必显式给出,下面给出一种求基函数的方法。
设有限元的形函数空间为PK=span{φi;1≤i≤n},两个分量的自由度分别为Di、Ei,将自由度表示为形函数的组合:
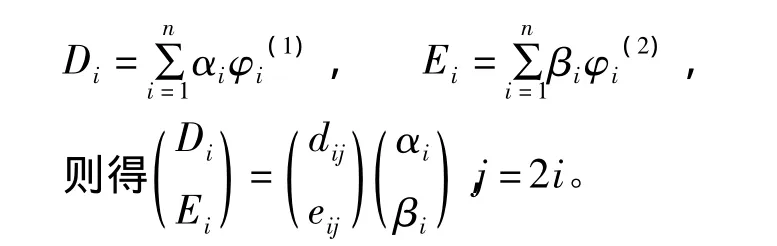

3 有限元算法与编程
3.1 单元编号和单元节点编号
单元编号和单元节点编号的原则是方便未知量求解,以及求解向量的使用。
单元节点编号的方法:
因为平面弹性问题是一个向量问题,因此在单元编号上和普通有限元方法单元节点编号是不同的。一般来说,按逆时针编号(顺时针也可以),按自由度组先第一分量、后第二分量编号,一个接一个自由度组连续编号。
(gij)en×en,1 ≤ i≤ ES,1 ≤ j≤ en。
下面是以CR元例,说明单元编号和单元节点编号,CR元的共有3组6个自由度,分别是三边ei的中点,如图1所示。
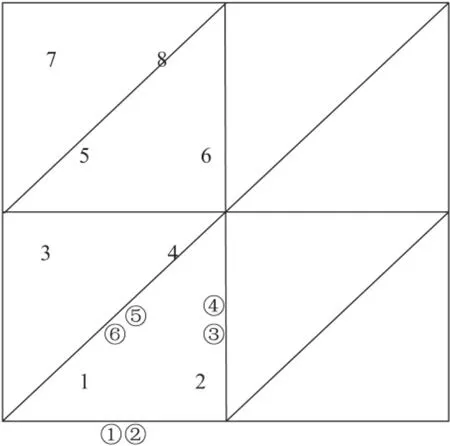
图1 单元和单元节点编号
3.2 单刚矩阵的形成:
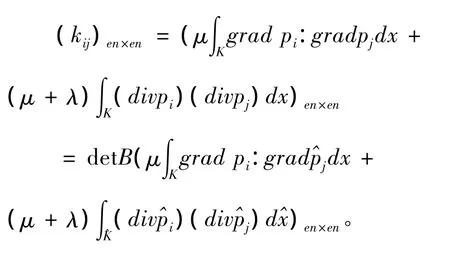
3.3 荷载向量的形成:
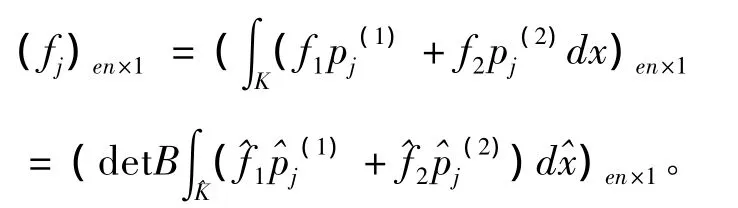
3.4 合成总刚矩阵:
设第m个单元的单刚矩阵AKj=(kij)en×en,它的总体单元节点编号是 m1,m2,L,men,那么它在总刚中的位置是:

3.5 合成总体载荷向量:
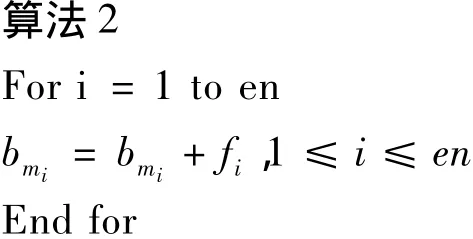
3.6 支撑条件
在形成总体刚度矩阵时还需要加入支撑条件,这里仅以固支条件为例给予说明。传统的方法是将总刚矩阵A的主对角线元素aij置为很大的一个数,如10308,这种满足支撑条件的方法会使得A的条件数变大,不利于迭代求解。事实上,只须将主对角线元素aii置为1,第i行、第i列其它元素置为0,对应的荷载列阵第i行的元素也置为0。这种支撑条件的优点是可以使A的条件数大大变小,因而有利于迭代法求解。

方程组求解,方法很多,有分解法、迭代法、共轭梯法等。
4 误差估计
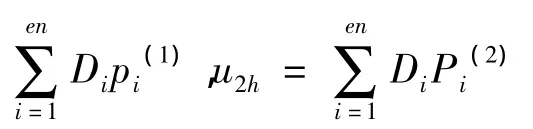


5 算例
算例1:考虑下面纯位移的齐次平面弹性问题:
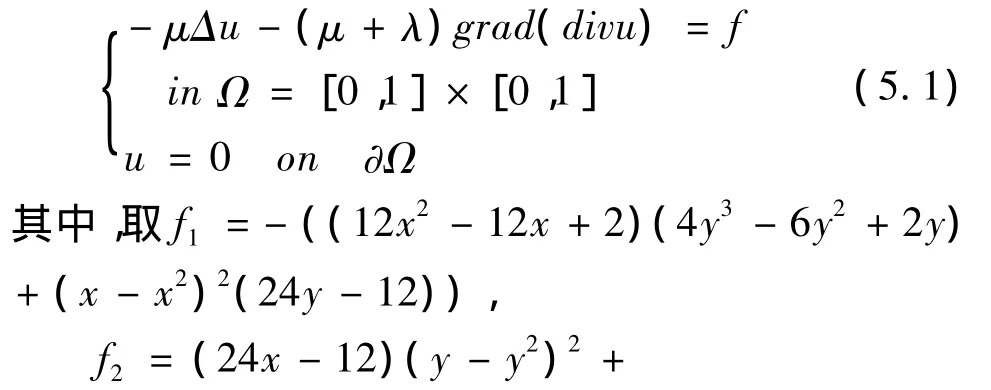

单元采用正则均匀剖分,在μ,λ不同取值下的0模、0模误差和1半模误差的计算结果分别见表一、表二和表三。
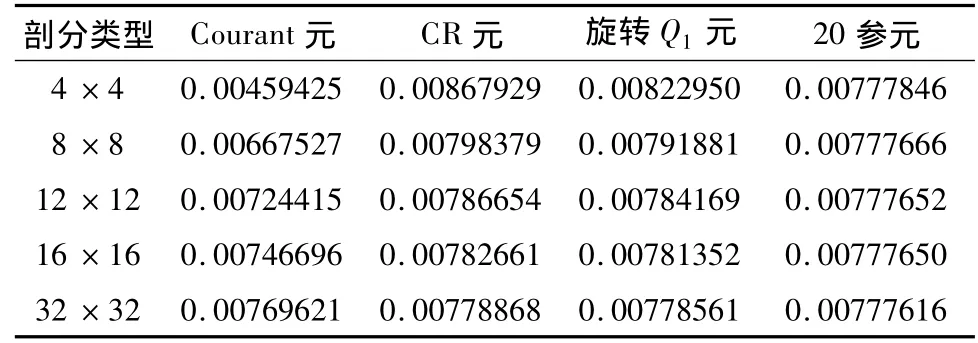
表一 解的0模(μ=λ=1)
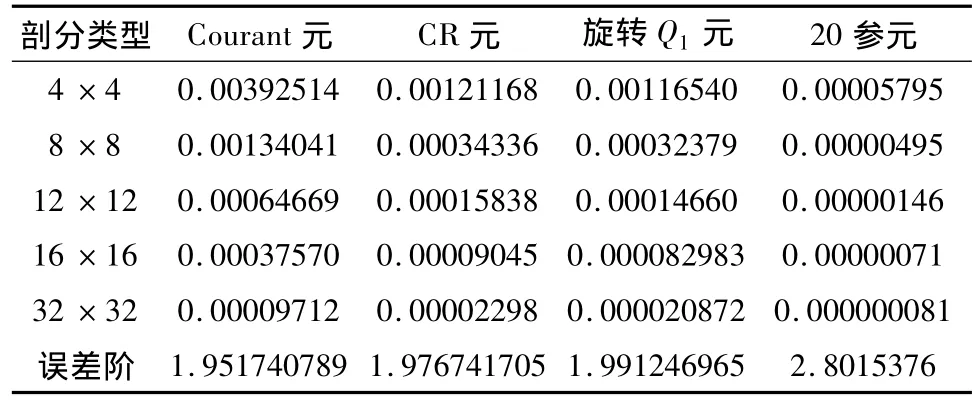
表二 计算精度(0模误差)表(μ=λ=1)
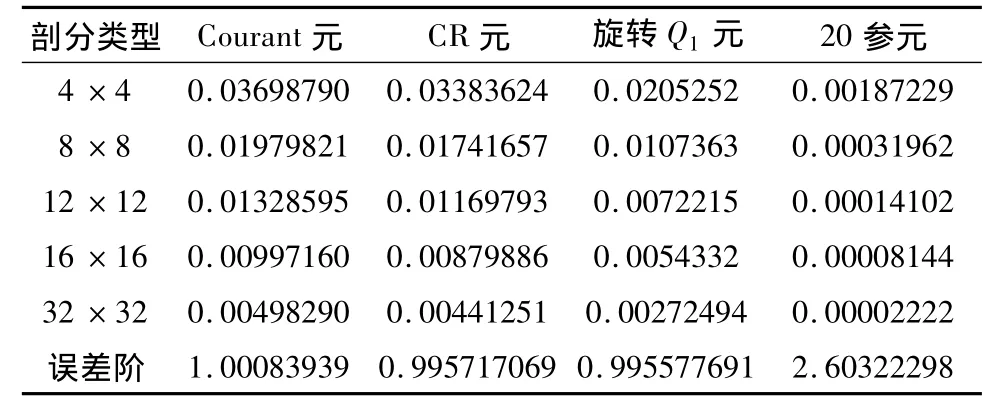
表三 计算精度(1模误差)表(μ=λ=100000)
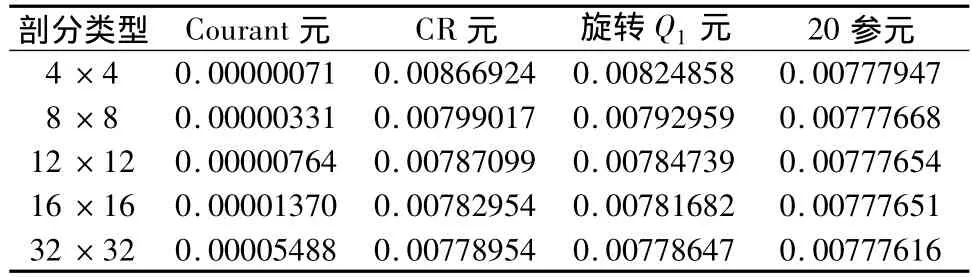
表四 解的0模μ=λ=1)
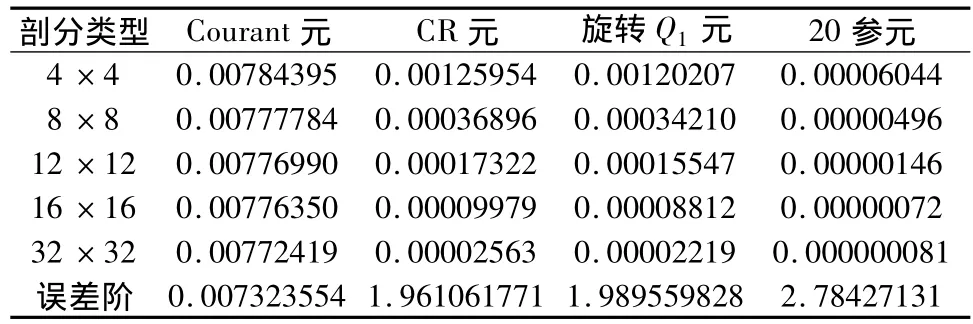
表五 计算精度(0模误差)表(μ=1,λ=100000)
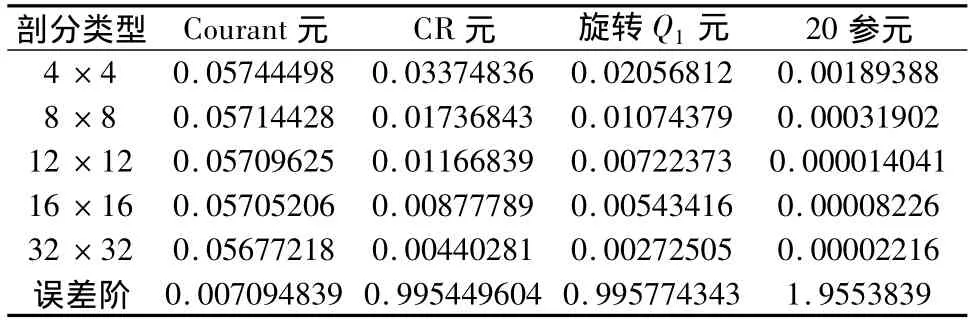
表六 计算精度(1模误差)表(μ=1,λ=100000)
从表四、表五、表六的数值结果我们可以看出:有限元方法在求解平面弹性问题的有效性。
[1]李开泰,黄艾香,黄庆怀.有限元法及其应用[M].北京:科学出版社,2006.
[2]刘尔烈,崔恩第,徐振铎.有限单元法及程序设计[M].天津:天津大学出版社,2002.
[3]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
