基于改进粒子群算法的风储联合系统多目标协同调度

代兵琪 王 哲 李春生

（1.青岛大学自动化工程学院，山东 青岛 266071；2.国网山东高密市供电公司，山东 高密 261500）

近年来，随着全球化石能源的大量消耗，能源枯竭和环境污染问题日益突出，因此，风力发电在世界范围内得到了快速发展。然而，风能不同于常规能源的是，其具有不确定性和间歇性的特点，这会使得风电功率波动很大，给大规模风电并网带来很大的挑战[1]。因此，减小风电场的输出功率波动，提高风电场的发电效益显得尤为重要。目前，国内外使用储能装置调度风电场运行的研究已经取得一定成果。文献[2]采用单一电池储能方式，提出利用超前控制策略，减小短期内风电功率的波动。文献[3]利用抽水蓄能装置风电场的弃风，来获得风电场的效益最大化。文献[4]利用混合储能装置，通过设计的控制器，可以合理控制储能元件的充放电全过程，有效平抑了风电场的输出功率波动。

本文基于抽水蓄能电站容量大的特点，给风电场配置一个小型抽水蓄能电站，建立了抽水蓄能与风电场联合运行的多目标协同调度模型。采用基于虚拟理想粒子的多目标改进PSO 算法进行求解，计算出一天内各时段的抽水蓄能装置功率最优分配，从而使风电场输出功率波动最小和发电效益最大。

1 多目标调度数学模型

风电场与抽水蓄能联合系统运行原理图如图1所示。当风能过剩时，可以利用多余的风能带动抽水蓄能的水泵将下水库中的水抽到上水库中，把风能以水的重力势能形式储存起来；当风能过小，不足以满足电网负荷要求时，通过抽水蓄能的水轮机利用上水库储存的水发电。这样，可以充分利用风能，降低风电场输出功率的波动，达到削峰填谷的目的，同时，又提高了风电场的发电效益。

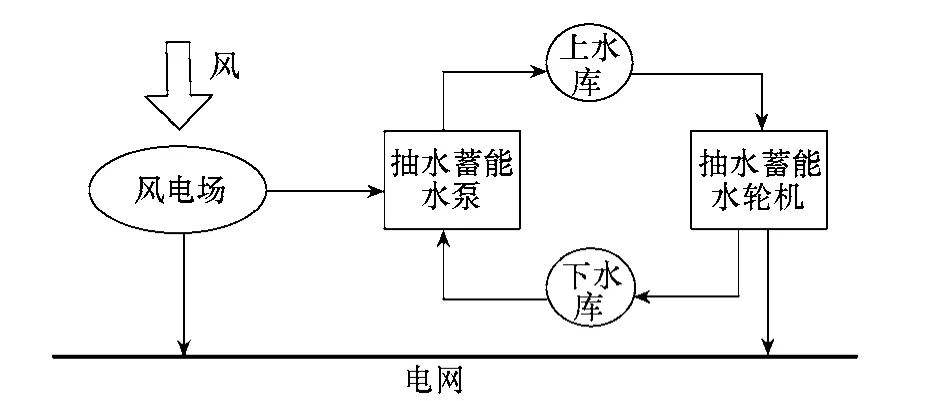
图1 风储联合系统原理图

1.1 目标函数

为减小风电场出力波动对电网的影响和使风电场发电效益最大，本文的目标函数选取风电场出力波动最小和风电场收益最大，把一天分为24 时段，以1h 为一个调度时段，把每个调度时段中储能装置的吸收和发出的功率作为优化变量。

1）以风电场出力波动最小为目标函数，则有

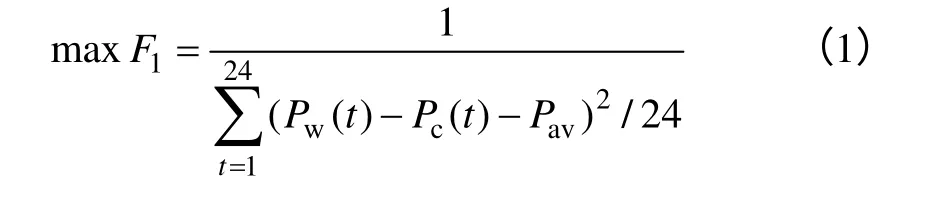
式中，Pw(t) 为t时间窗口风电机组出力；Pc(t)为t时间窗口系统中储能装置吸收或发出的功率（正值为吸收功率，负值为发出功率）；Pav为风储系统吸收和发出功率的平均值，可由式（4）求得：

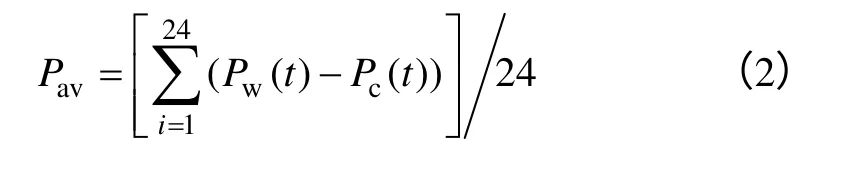
2）以最大化风电场发电效益为目标函数，则有

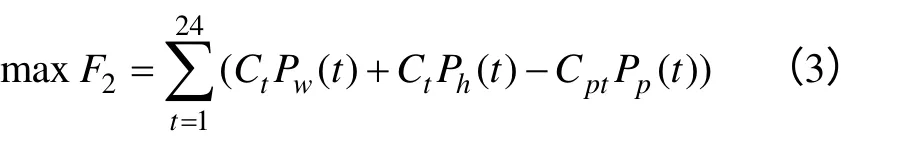
式中，Ct为t时间的电价；Cp为吸收电能所需费用。

1.2 约束条件

1）电网功率约束条件

式中，Pe(t)为t时刻风电场输送至电网的功率，Pmin和Pmax分别为电网限制的最大和最小功率。

2）抽水蓄能约束条件

（1）库容能量平衡方程

式中，Ec(t)为t时刻抽蓄装置容量；Pp(t)为t时刻抽蓄装置的抽水功率；Ph(t)为t时刻抽蓄装置的发电功率；Δt为抽水或发电时间。η1和η2分别表示电能转化为水的势能和水的势能转化为电能的效率。

（2）抽蓄装置功率和容量约束，分别为

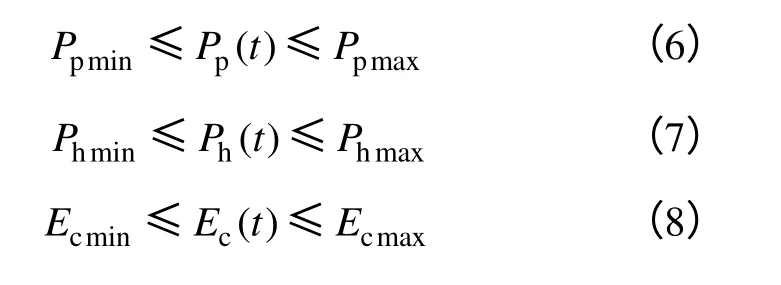
式中，Pp(t)为t时刻抽蓄装置的抽水功率；Ph(t)为t时刻抽蓄装置的发电功率；Ec(t)为t时刻抽蓄装置的容量；Ppmin、Phmin和Ecmin为相应变量的最小值，Ppmax、Phmax和Ecmax为相应变量的最大值。

2 模型求解方法

2.1 标准粒子群优化算法

在标准粒子群算法中，假设在D维搜索空间中，有N个粒子以一定的速度飞行，粒子位置可表示为：xi=(xi1,xi2,...,xiD)， 因此其速度可以表示为vi= (vi1,vi2,… ,viD)。每次迭代中，粒子将跟踪的两个极值，一个是单个粒子所找到的最优位置Pi，另一个是整个粒子群的最优位置Pg，粒子根据以上两个位置来更新自己的位置，其更新公式为：

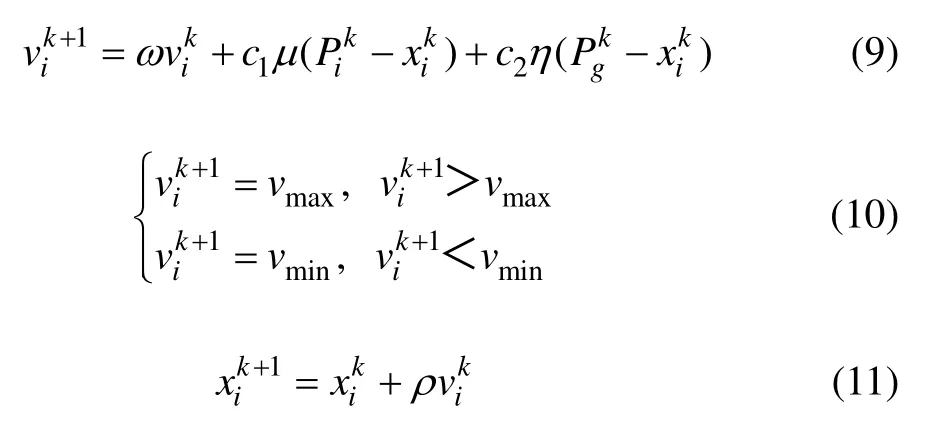
式中，ω为惯性权重系数，c1是粒子自身加速系数；c2是全局加速系数；μ和η是在[0，1]区间的随机数；ρ是约束因子。

2.2 改进粒子群算法

基本粒子群算法在迭代进行到后期时会出现全局搜索能力不足,效果较差的缺点,从而难以找到全局最优解。

为了提高算法的性能，含时变加速系数的改进粒子群算法对速度更新公式进行了改变，加入了新的迭代量，速度更新公式如下。

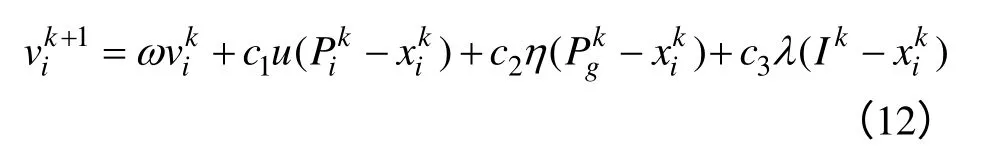
式中，Ik为第k次迭代中的最优解；λ是[0，1]区间的随机数，加速系数根据下面的公式进行更新。

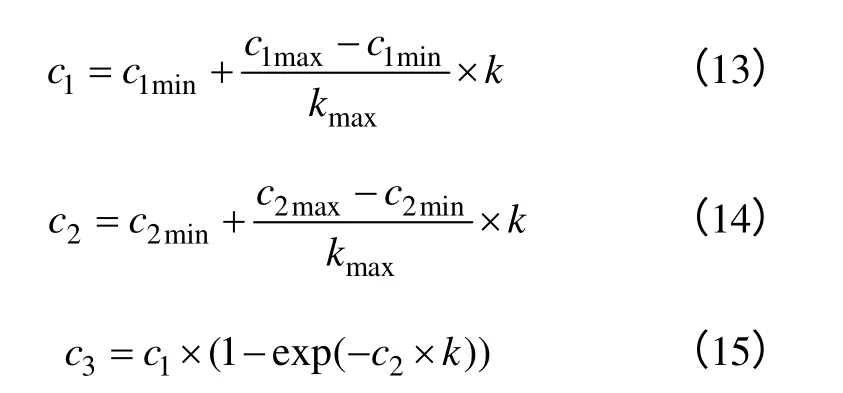
式中，c1min=c2min= 0.5，c1max=c2max= 2，kmax为最大迭代次数。

2.3 基于虚拟理想粒子的多目标改进粒子群算法

1）算法基本原理

在多目标优化问题中，最关键的一步就是折衷解的选取，现有折衷解的求解方法是在事先得到的帕累托最优集中，根据实际需要进行选取。为了避免复杂的比较，简化程序步骤，本文采用一种多目标改进粒子群算法，该算法构造了一个虚拟的理想粒子，其他粒子通过与该粒子的几何平均距离来判断自身位置的优劣，如图2所示。

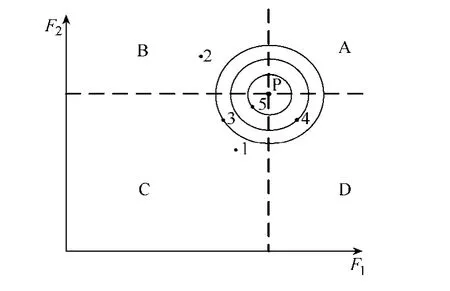
图2 算法基本原理

图2中将两个单目标函数分别求解，得到的最大值F1max和F2max作为理想粒子的坐标，记为P(F1max,F2max)。由于同时考虑2 个目标时，相互之间的约束条件不同，因此，点P是一个虚拟的点。图2中的坐标系被虚线划分成了ABCD 四个区域，其中，区域A 是实际多目标问题中，不可能优化到的理想区域，而其他区域可以优化得到。如图2所示，取坐标系中的5 个经过优化得到的点，根据这5 个点与理想粒子点P的几何平均距离，可以看出，点5 最优，也就是实际问题中，最终要选取的折衷解。

在基于虚拟理想粒子的多目标改进PSO 中，虚拟点P作为优化目标，是粒子位置更新的评判标准，它指引着新粒子无限地去靠近理想解。该算法只需适当修正目标函数，将多目标优化问题简化为单目标优化问题，有效了程序的步骤。因此，基于虚拟理想粒子的多目标改进粒子群算法的目标函数可构造为

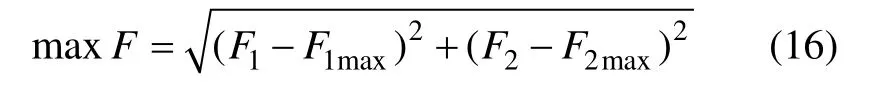
2）算法流程

基于虚拟理想粒子的多目标改进粒子群算法的流程如图3所示。

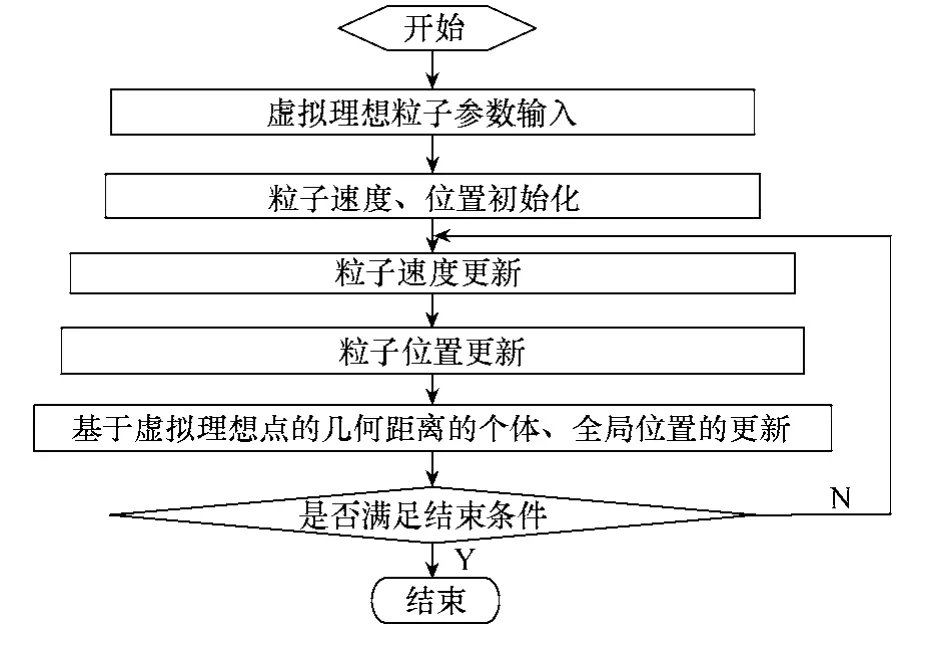
图3 算法流程图

3 算例分析

本文以某装机容量为12 MW 的风电场系统为例，当风场的风况进入稳定期时，风场每天的风况大体相似，风电场的某日出力情况如图4所示，假定电网的限制功率为3MW≤Pi≤8MW，储能装置初始储能Ec（1）为0，风力上网定价由式（17）确定。算法中，初始种群规模N取40，迭代次数为100 代，其他参数设置见表1。

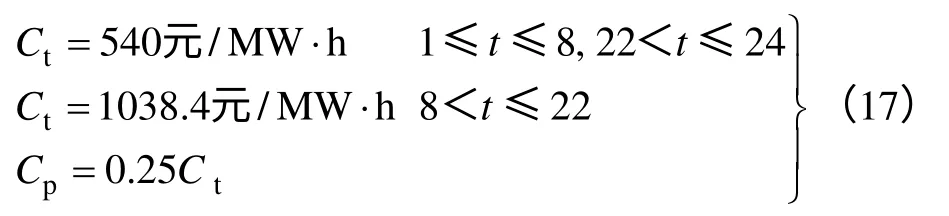
根据上述参数，运用改进粒子群算法求解该算例，得到运行结果如图5所示。

由图5中的Pareto解集可以得出，经过运行优化后，联合风电场输出功率方差的倒数随着风电场的收益增大而减小，使两个目标函数不能同时达到最 大。本文基于虚拟理想粒子的多目标改进PSO进行优化时，公式（16）中的F1max和F2max的取值如表2所示。

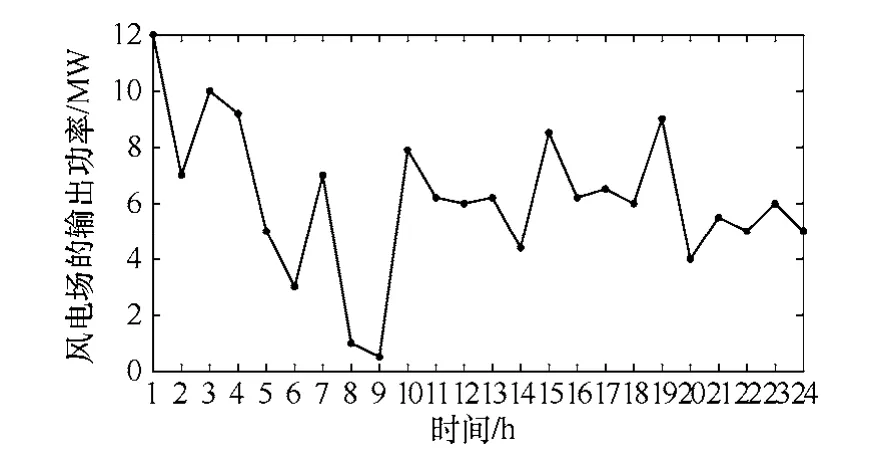
图4 风电出力曲线

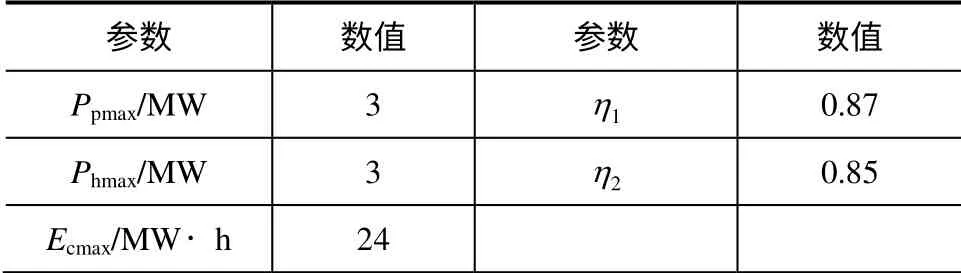
表1 模型参数设置

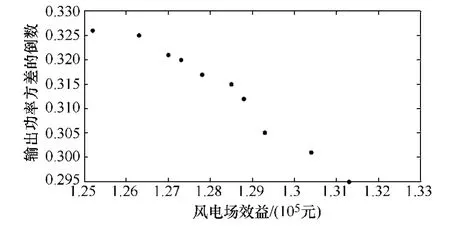
图5 迭代100 次后的Pareto 解集

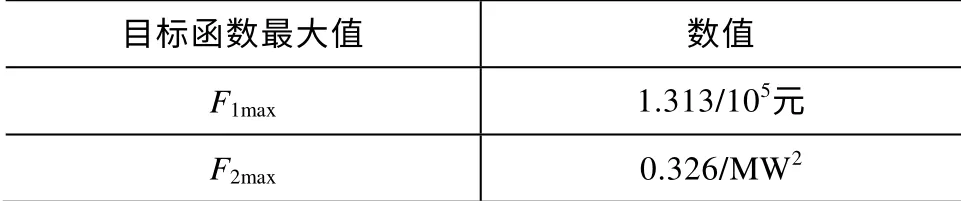
表2 多目标PSO 优化时F1max 和F2max 取值

经过多目标改进PSO 算法优化后，风电场的收益为128764 元，比仅有风电场时的收益124870 元多了3894 元。

风电场在各时段的输出功率如图6所示。可以看出联合优化运行后的输出功率的方差为3.2MW2，远小于仅有风电场时输出功率的方差6.6MW2。

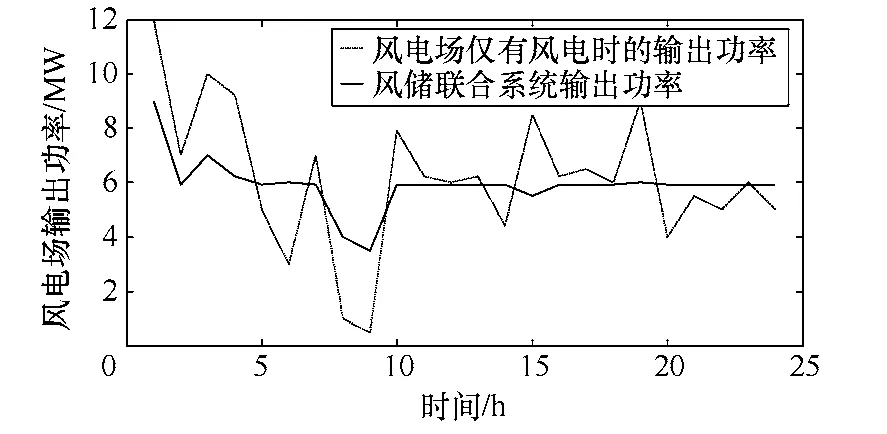
图6 风储联合系统运行后输出功率

通过上述分析可以看出，风储联合运行，不仅可以减小风电场输出频率对风电出力波动的影响，同时还使风电场获得了更大的效益。

4 结论

本文提出了基于改进粒子群算法的风储联合系统多目标协同调度模型。该模型以风电场输出功率波动最小和发电效益最大为目标，以储能装置的吸收和输出功率和容量为约束条件。从算例结果可以看出，该模型有效平滑了风电场输出功率和增加了风电场效益，提高了风电利用率，为风电更大程度地参与电力系统调度提供了一个有效方案，同时，也验证了基于虚拟理想粒子的多目标改进粒子群算法解决优化问题的可行性和有效性。但是，该模型未考虑风电场风速预测技术，在后期工作中有待进一步研究。

[1] 李蓓,郭剑波.平抑风电功率的电池储能系统控制策略[J].电网技术,2012,36(8): 38-43.

[2] 于芃,周玮,孙辉,等.用于风电功率平抑的混合储能系统及其控制系统设计[J].中国电机工程学报,2011,31(17): 127-133.

[3] 丁明,徐宁舟,毕锐.用于平抑可再生能源功率波动的储能电站建模及评价[J].电力系统自动化,2011,35(2): 66-72.

[4] 潘文霞,范永威,杨威.风-水电联合优化运行分析[J].太阳能学报,2008,29(1): 80-84.

[5] 温令云,龚文杰,张伟,等.基于CROA 的智能电网电动汽车有序充放电策略研究[J].青岛大学学报(工程技术版),2013,28(3): 23-26,36.

[6] 杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11): 1-5.

[7] 马静,石建磊,李文泉,等.基于功率多频率尺度分析的风光水气储联合系统日前调度策略[J].电网技术,2013,37(6): 1491-1498.

[8] 张步涵,曾杰,毛承雄,等.电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术,2006,30(15): 54-58.