Van der Pol型自激单摆的张弛振荡特性*
2015-05-28郑远广鲍丽娟
郑远广 鲍丽娟
(南昌航空大学数学与信息科学学院,南昌 330063)
引言
自激振动是典型的非线性现象,广泛地存在于自然界和工程系统中[1,2].在自激振动系统中,其自身的阻尼不断消耗系统的能量,要维持周期性振动,系统需要从外界获得周期性的能量补充.然而外界提供的只是恒定的能源,系统必须通过自身特有的激发和反馈机制把这种恒定的能源转化成系统周期性的能量补充,从而维持其周期性振动.与自由振动和受迫振动相比,自激振动系统有如下显著特点:自激振动系统是耗散系统,振动过程中存在能量的消耗和补充;外界提供的能源是恒定的,外界对系统补充的能量是受系统自身特有的激发和反馈机制控制,因此系统是自治的;自激振动的周期和振幅仅与系统自身的参数有关,与初始条件无关.
自激振动常常对工程系统产生不利影响.在机械加工过程中,由于车刀与切屑之间的滑动摩擦力与其相对速度存在非线性关系,这导致切削过程中会发生自激振动,降低加工质量和效率[3].结冰输电线的横截面是非圆形的不规则形状,在风力的作用下会产生与风速成非线性关系的阻力和升力,在一定条件下会导致输电线产生自激振动,称为输电线舞动,这严重影响输电线的使用寿命[4].与此相类似,高层建筑和大型桥梁,在风力作用下也会发生自激振动,这可能会导致灾难性的后果.在输水管道中,由于水流与管道之间的非线性耦合作用,也可以导致自激振动的发生,从而影响流速和发出噪声[5].另一方面,自激振动也存在有利的一面,比如,射流在煤矿开采、石油钻井、以及岩石切割等方面具有广泛应用,可以利用流体自激振动原理来提高射流的速度,从而提高其工作效率[6].
在工程实践中,为了消除有害的自激振动和利用有益的自激振动,就必须研究自激振动现象的产生机制.van der Pol光电系统是自激振动系统的原形,其中的自激振动现象得到了广泛的研究[7,8].含van der Pol型自激项的单摆系统是典型的含自激励的机械系统,对其自激振动现象进行研究有助于了解实际机械系统中自激振动的产生机制.该van der Pol型自激单摆系统的平衡点是不稳定的,当摆幅较小时,系统从外界吸收能量增加摆幅,而当摆幅较大时,系统消耗能量抑制摆幅,从而系统发生稳定的周期运动.文献[9]的研究表明自激单摆系统存在丰富的动力学现象,受到外界激励时,可以发生混沌运动.文献[10]考察了高频横向和纵向激励对自激单摆系统振动的影响,发现横向的高频激励能有效抑制系统的自激振动,然而在纵向激励下,自激振动一直存在.文献[11,12]讨论了时滞与高频激励联合作用对自激单摆系统振动的影响,发现加入时滞后有利于抑制系统的自激振动.当阻尼值较大时,该自激单摆系统发生张弛振荡(relaxation oscillation),其中快速运动过程和慢速运动过程交替出现.张弛振荡现象首先是在van der Pol电路系统中发现的[7],其后,人们发现张弛振荡现象广泛地存在于生态系统[13]、生理系统[14]、化学系统[15]等现实系统中.文献[13]运用几何方法研究了捕食与被捕食系统中的张弛振荡现象,得到系统发生张弛振荡的充分条件.文献[14]利用张弛振荡特性解释了心脏的电活动规律.文献[15]基于数值方法分析了化学系统中的振动现象,发现当参数变化时,系统由周期振动变为张弛振荡.
张弛振荡的存在性及其特性通常与系统的结构和参数有关,然而至今为止,对van der Pol型自激单摆的张弛振荡特性的研究工作还很少.基于这一事实,本文将考察含大阻尼的van der Pol型自激单摆的张弛振荡的存在性及其特性.在下一节首先介绍van der Pol型自激单摆的系统模型.接着在第三节讨论张弛振荡的存在性及其特性.在第四节进行数值算例分析.最后在第五节对全文进行总结.
1 系统模型
van der Pol型自激单摆系统模型为

其中y∈(-π,π)变量表示单摆离开垂直位置的摆角,k和h是取值O(1)的系统参数,为较大的阻尼系数,且0<ε≪1为小参数.引入新的时间变量s和变量-h sin y(t),方程(1)变为

这里一点表示对时间t的导数.由于0<ε≪1为小参数,y(t)变化速度比较快,称为快变量,而 x(t)称为慢变量,方程(2)为典型的快-慢系统.若再引入时间变量t,则方程(2)变为
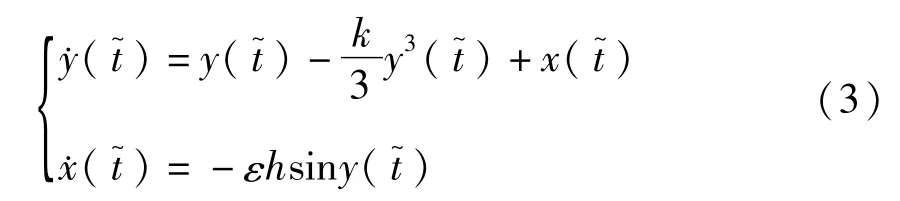
这里一点表示对时间的导数.在方程(3)令ε→0,则得到仅关于快变量的快子系统

其中变量x看成系统中的参数.
几何奇异摄动理论是分析快-慢系统动力学行为的有效工具[16,17].该理论体系主要包括 Tikhonov和Fenichel关于慢变流形和不变流形的存在性及其性质的系列定理[18-20].Tikhonov定理指出稳定的慢变流形对解轨线具有吸引性,而不稳定的慢变流形对解轨线具有排斥性.Fenichel系列定理主要讨论了不变流形的存在性及其性质,指出慢变流形是不变流形的近似,并进一步描绘了在慢变流形附近的解轨线结构.几何奇异摄动理论表明快-慢系统的动力学行为与系统的慢变流形的结构紧密相关.因此,为求得系统的动力学行为,关键的步骤是要确定慢变流形的结构,包括其形状、稳定性、分岔点的类型和分布.
2 系统的张弛振荡特性
根据几何奇异摄动理论,系统(2)的慢变流形为
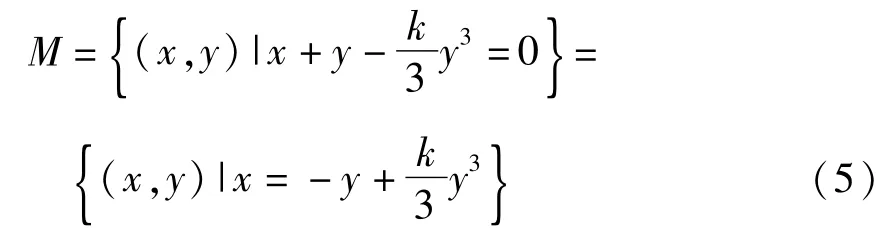
可见慢变流形M就是快子系统(4)的奇点集合.对于0<k=O(1),慢变流形为S-形的曲线,见图1.为确定慢变流形M的结构,求得快子系统(4)在平衡点 y=y(x)(其中 y(x)满足 x+y(x)=0)的唯一特征根为λ=1-ky2.因此,根据快子系统(4)的平衡点的稳定性,慢变流形M可分成如下三部分
见图1,上下粗线为稳定的慢变流形部分M1和M3,中间的虚线为不稳定的慢变流形部分M2,点


和

是慢变流形上的两个Saddle-node分岔点.

图1 慢变流形M=M1∪M2∪M3的结构,其中M1∪M3和M2分别为稳定和不稳定的慢变流形部分,S1和S2是Saddle-node分岔点Fig.1 The structure of slow manifold M=M1∪M2∪M3,where M1∪M3 and M2 are the stable and unstable slow manifold,S1 and S2 are Saddle-node bifurcation points
得到了系统慢变流形的结构后,就可以运用几何奇异摄动理论分析系统的动力学行为.根据几何奇异摄动理论,稳定的慢变流型M1∪M2对解轨线具有吸引性,当解轨线被吸引到稳定的慢变流形上时,由于 ˙y(t)≈0,因此解轨线将沿着慢变流形缓慢地运动.当解轨线被吸引到上半部分的慢变流形M1上时,由于 y(t)∈M1时有 ˙x=-h sin y(t)<0,所以解轨线自右向左运动.当解轨线到达鞍结分岔点S1时,解轨线离开不稳定的慢变流形M2,而被吸引到下半部分稳定的慢变流形M3上,这时有˙x(t)>0,所以轨线自左向右运动.当解轨线到达鞍结分岔点S2时,又被吸引到上半部分的慢变流形M1上,见图2(a).由此系统发生张弛振荡,见图2(b).
对于大阻尼系数α,有.从系统(2)的第一个方程可以看到,当解轨线不在慢变流形上时,有,因此,张弛振荡的快速运动过程将在瞬间完成.张弛振荡的慢速运动过程经过的慢变流形部分为

图2 系统(3)的张弛振荡,(a)解轨线,(b)时间历程图Fig.2 Relaxation oscillation of system(3),(a)Solution trajectory,(b)Time series

和

这里Y*>0满足方程

从而可以求得张弛振荡解轨线的近似表达式为

从解轨线的近似表达式可以看到,解轨线的形状与慢变流形的形状相关,仅由参数k的值决定.
由于张弛振荡的快速运动过程在瞬间完成,所以张弛振荡的周期主要由慢速运动过程所需要的时间决定.把代入系统(2)的第二个方程得

因此,张弛振荡的周期为

由周期的近似表达式可见,其周期T与参数k和h相关,且是h的递减函数.
总结以上分析,可以得到如下结论
结论1: 对于大阻尼α和参数0<k=O⑴,系统发生张弛振荡运动;张弛振荡轨线的近似表达式为(6)式,其形状仅与参数k相关;张弛振荡周期的近似表达式为(7)式,其与参数k和h相关,且是h的递减函数.
依据以上理论分析结果,可以得到van der Pol型自激单摆的运动特性如图3所示.

图3 van der Pol型自激单摆的运动特性,y表示摆角Fig.3 Dynamics of the pendulum with van der Pol type self-excitation,where y represents the angle of the pendulum
从图3可见,当摆角y在区域和时,摆球缓慢运动;而摆球快速通过区域;点为快速运动和慢速运动的分界点.
3 算例分析
为进一步了解张弛振荡解的特性和验证理论分析的正确性,本节进行算例分析.取大阻尼值α=30和常用的参数值 k=0.75、h=1,则方程(2)为

系统的慢变流形为

由于k=0.75>0,慢变流形 M为 S-形曲线,根据结论1可知系统发生张弛振荡,这与数值结果相符,见图4,这里数值结果是在MATLAB中用刚性方程积分器ODE23S算得的,其中RelTol=1e-10和 AbsTol=1e-8.
通过方程求得 Y*=2.3094>0,由式(6)求得张弛振荡的近似表达式为

此近似表达式与数值结果相吻合,见图4(a).
由式(7)求得张弛振荡的周期为

理论值与数值结果相吻合,见图4(b).

图4 系统(8)的张弛振荡,(a)解轨线,(b)时间历程图Fig.4 Relaxation oscillation of system(8),(a)Solution trajectory,(b)Time series
4 结论
自激振动对机械系统的性能具有重要影响,研究机械系统中的自激振动机制有助于消除有害的自激振动而利用有益的自激振动.van der Pol型自激单摆系统是典型的含自激励的机械系统,本文阐述了其中张弛振荡的产生机制,并给出了张弛振荡解的近似表达式.研究表明当系统发生张弛振荡时,单摆快速通过平衡位置,而在远离平衡位置的一段区域上停留较长时间.本文的研究结果可以在一定程度上说明一般的自激机械系统中张弛振荡的产生机制,可以为工程实践提供一定的理论指导.
1 Van der Pol B.Forced oscillations in a circuitwith non-linear resistance(reception with reactive triode).The London,Edinburgh,and Dublin Philosophical Magazine and Journal of Science Series7,1927,3:65~80
2 贾启芬,于雯,刘习军等.多自由度分段光滑非线性系统的近似解-中华文物龙洗的自激振动.力学学报,2004,36(3):373~378(Jia Q F,Yu W,Liu X J,Wang D J.Approximate analytical solution of the piecewisesmooth nonlinear systems of multi-degrees-of-freedom-The self-excited vibration of the chinese cultural relic dragon washbasin.Acta Mechanica Sinica,2004,36(3):373~378(in Chinese))
3 Stepan G,SzalaiR,Mann B P,etal.Nonlinear dynamics of high-speed milling,analyses,numerics and experiments.Journal of Vibration and Acoustics,2005,127(2):179~203
4 蒋扇英,徐鉴.奇异摄动方法在输电线非线性振动问题中的应用.力学季刊,2009,30(1):33~38(Jiang S Y,Xu J.Singular perturbation method and its application in nonlinear systems with fast and slow variables coupling.Chinese Quarterly ofMechanics,2009,30(1):33~38(in Chinese))
5 Brika D,Laneville A.Vortex-induced vibrations of a long flexible circular cylinder. Journal of Fluid Mechanics,1993,250(4):481~508
6 王萍辉,马飞.自激振动空化射流振动分析试验.机械工程学报,2009,45(10):89~95(Wand P H,Ma F.Vibration analysis experiment of self-resonating cavitating water jet. Journal of Mechanical Engineering,2009,45(10):89~95(in Chinese))
7 Van der Pol B.On"relaxation-oscillations".The London,Edinburgh,and Dublin Philosophical Magazine and Journal of Science Series7,1926,2:978~992
8 萧寒,尹小波.多自由度van der Pol型系统振幅增大控制.动力学与控制学报,2008,6(1):32~34(Xiao H,Yin X B.Enlarging amplitude control of van der Pol type with multidegree of freedom system.Journal of Dynamics and Control,2008,6(1):32~34(in Chinese))
9 Ambika G,Babu Joseph K.Transition to chaos in a driven pendulum with nonlinear dissipation.Pramana Journal of Physics,1988,31(1):1~8
10 Bourkha R,Belhaq M.Effect of fast harmonic excitation on a self-excited motion in Van der Pol oscillator.Chaos,Solitons&Fractals,2007,34(2):621~627
11 Belhaq M,Sah SM.Horizontal fast excitation in delayed van der Poloscillator.Communications in Nonlinear Science and Numerical Simulation,2008,13(8):1706~1713
12 Sah SM,Belhaq M.Effect of vertical high-frequency parametric excitation on self-excited motion in a delayed van der Pol oscillator.Chaos,Soliton& Fractals,2008,37(5):1489~1496
13 Liu W S,Xiao D M,Yi Y F.Relaxation oscillations in a class of predator-prey Systems.Journal of Differential Equations,2003,188(1):306~331
14 Van der Pol B,Van der Mark J.The heartbeat considered as a relaxation oscillation,and an electrical model of the heart.The London,Edinburgh,and Dublin Philosophical Magazine and Journalof Science Ser.7,1928,6:763~775
15 Chumakov G A,Chumakova N A.Relaxation oscillations in a kineticmodel of catalytic hydrogen oxidation involving a chase on canards.Chemical Engineering Journal,2003,91(2-3):151~158
16 Verhulst F.Singular perturbation methods for slow-fast dynamics.Nonlinear Dynamics,2007,50(4),747~753
17 郑远广,王在华.含时滞快-慢系统的若干动力学问题.力学进展,2011,41(4):400~410(Zheng Y G,Wang Z H.Advances in dynamics of slow-fast systems with time delay.Advances in Mechanics,2011,41(4):400~410(in Chinese))
18 Tikhonov A N.Systems of differential equations containing a small parameter multiplying the derivative.Matematicheskii Sbormik,1952,31(73):575~586
19 Fenichel N.Geometric singular perturbation theory for ordinary differential equations.Journal of Differential Equations,1979,31(1):53~98
20 Jones C K R T.Geometric singular perturbation theory in dynamical systems.Berlin:Springer-verlag,1994
