含间隙弹簧振动系统的非线性模态特性*

李艳清 江俊

（西安交通大学机械结构强度与振动国家重点实验室，西安 710049）

引言

线性振动系统的模态在工程实际系统的分析中发挥着重要作用，如：避免结构的共振发生，利用模态叠加法求解结构的响应等.Rosenberg［1，2］基于线性模态的思想提出了非线性模态的定义：保守系统的模态是周期解，模态曲线在系统总能量曲线所围得闭区域是单值函数，系统解同时通过平衡点，且同时到达最大值点.在非线性系统中，非线性模态也有很重要作用，当外激励频率和模态频率相近时，系统同样会产生共振行为［3］；在一定条件下，非线性模态的合成解可以近似表示原系统的准确解［4，5］，因此求解并研究非线性模态，特别是多余模态，如何影响系统响应有着实际的应用意义.

确定非线性模态主要基于三种思想：一种是先将非线性系统预处理，使其近似看作线性系统，然后求解线性系统的模态，在此基础上将模态解展开为泰勒级数，通过参数变化来近似确定原系统的非线性模态［6］，但是此方法不能获得系统的模态频率，并且非线性模态的精度与泰勒级数的阶数有关；另一种是采用Poincaré截面图和动力系统不变流行理论构建求解分段线性振动系统的非线性模态，并在极坐标系下将其级数展开，确定系统的不同模态，模态的频率-振幅的关系［7］，此方法只能获取在平衡点附近的系统模态以及频率；最后一种是采用扰动方法求解系统的非线性模态，并获取相应的多余模态［8］，用级数近似拟合突变刚度，将分段刚度系统看作光滑系统来近似求解.

系统的参数对非线性模态影响很大，相对于相似模态运动，多余模态的运动形式多样化，包括模态的数量和振动方式等，因此非线性模态会出现内共振［9］和分岔［8，10］等.文献［11］分析了两自由度分段线性系统的模态形式及分岔的条件.文献［12］分析了单自由度双线性刚度系统中，间隙的大小和数目以及系统刚度对模态频率的影响，采用线性系统的模态参数扰动可以近似获得弱非线性系统的模态.在强非线性系统中，文献［13］基于不变流行概念，采用Galerkin方法求解偏微分方程获取大振幅强非线性振动系统的非线性模态.文献［14］采用实验方法验证系统的非线性模态和多余模态，模态分岔和内共振条件.一般地，对于分段光滑系统可以采用先对系统刚度［6，8］或模态运动区域［7］进行分析，然后再求解系统的模态，而模态解的精度由预处理的刚度或模态区域决定.

本文主要针对分段光滑线性两自由度系统的非线性模态进行研究，该系统在位形空间不同区域内的运动由不同的具有线性刚度的子系统控制.本文将直接求解各个子线性系统的相应模态，然后通过在分段刚度变化处进行组装来获取系统的非线性模态，而系统的模态频率则通过采用加权平均的方法获得.最后，本文将基于理论分析的结果，采用数值计算的方法寻找系统的多余模态，并分析多余模态与同、异相模态的关系.

1 系统模型

本文研究的系统模型是一个两自由度具有分段阶跃刚度、无阻尼的弹簧-质量块系统（见图1）.两质量块与地面光滑接触，两弹簧为含间隙弹簧，x1＝0和x2-x1＝0分别为两弹簧刚度发生变化的分界点.当振子位移小于分界点时，弹簧间隙闭合，刚度为 ki，i＝1，2；当振子位移大于分界点时，弹簧间隙分开，刚度为 ki-εi，其中 εi，i＝1，2，是弹簧间隙引起的系统刚度的变化量（见图2）.系统的运动方程为：

图1 两自由度分段刚度模型Fig.1 DOFmodelwith piecewise stiffness

其中

m1和m2分别为两振子的质量，其对应的无量纲方程为：

其中

因本文只分析刚度变化对模态的影响，所以在分析系统模态时，不失一般性，取单位质量，即m1＝m2＝1.0，则可得：

图2 模型在位形空间中不同区域内的刚度取值，直线分别为x1＝0和x2-x1＝0Fig.2 The stiffness values in different regions of configuration space for themodel，lines represent x1＝0 and x2-x1＝0 respectively

图2中椭圆曲线表示系统的能量曲线，在保守系统中，两振子在能量曲线所围的封闭区域内振动.当质量块在能量线上运动时，系统的动能为零，势能取最大值；当质量块在封闭区域内振动时，系统同时具有动能和势能，但总能量恒定.当x1＝0和x1＝x2两弹簧变形量为零，为弹簧刚度变化的分界线，此分界线将质量块运动分为了四个区域，在不同区域内系统的刚度取不同值，且在分界直线处发生变化.当振子在第一个区域内时，两弹簧同时处在拉伸状态，间隙张开，因此刚度减小，这时两弹簧的刚度分别为 k1-ε1，k2-ε2；在第二个区域内，弹簧1处于压缩状态，间隙闭合，刚度为k1，此时弹簧2仍处于拉伸状态，间隙张开，刚度为k2-ε2；在第三个区域内，两弹簧同时处于压缩状态，间隙闭合，两弹簧的刚度分别为k1，k2；在第四个区域内，弹簧2处于压缩状态，间隙闭合，刚度为k2，而弹簧1处于拉伸状态，间隙张开，刚度为k1-ε1.可以看出：振子在不同的区域内，两弹簧刚度的取值不同，对应的振幅也不同.

2 非线性模态的求解

2.1 非线性模态运动的初始位移

模态运动是指两个质量块同时通过平衡点，即间隙分界点，且同时达到最大位移点的运动.为此假设模态运动的解形式为：

其中，当A、B符号相同时，表示同向模态运动，两振子的相位差为0.当A、B符号相反时，表示反相模态运动，两振子的相位差为π.将解（4）代入方程（1）中可得：

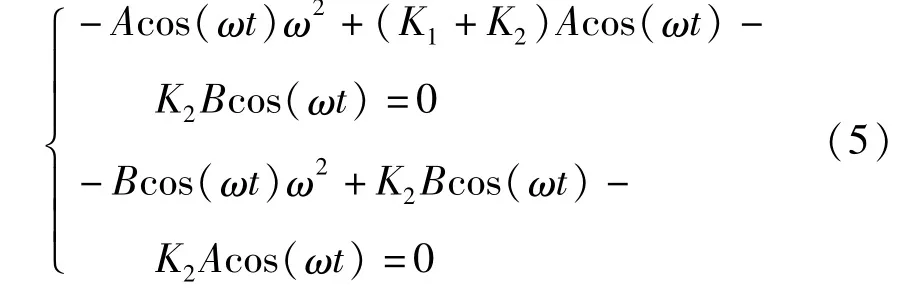
振幅A、B和ω为待求的值，其中幅值还需满足系统的能量方程.

在保守系统的运动过程中，无初始速度的系统振子，系统的动能为零，机械能等于两振子的弹性势能之和，即：

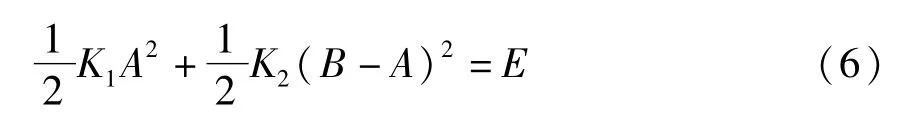
其中E为系统的机械能.

根据最小势能原理可以得到控制方程：

其中V为系统的势能，x＂2和x′2分别为x2对x1的二阶导数和一阶导数，Vx1和Vx2分别为在能量曲线上对x1和x2求导.Vx1和Vx2满足以下关系

将（8）代入控制方程（7）中可得：

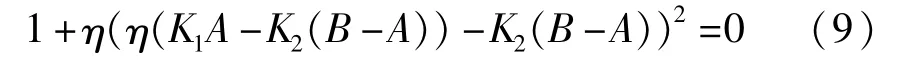
其中η＝x′2是x1归一化后，系统的模态解，表示模态曲线在位形空间中的斜率.如果系统的模态曲线为一次函数，则 η为常数，有 x＂2＝η′＝0.

由（2）和（3）可知，振子在不同位置，刚度 K1和K2的取值不同，其对应的幅值也不同.由能量方程（6）和控制方程（9）可以求解得模态解的振幅A和B.其将作为数值求解系统非线性模态的初始位移.

2.2 非线性模态频率的求解

方程（5）中公因子 cos（ωt）是关于 t的变量，若方程（5）恒为零，其对应系数为零，可得如下关于振幅比A／B和ω的方程组：

采用带入消元法可得到关于ω的方程：

方程（10）是关于ω2的二次方程有两个解，分别为：

在图2中不同的区域内，K1和K2取值不同.将式（2）和（3）中的第一个值或第二个值代入公式（11）可求得系统模态频率的最大值：

或最小值：

为求解该分段光滑线性系统的近似模态频率，本文定义如下加权平均刚度：

将（13）代入（11）可求得系统的模态频率为：

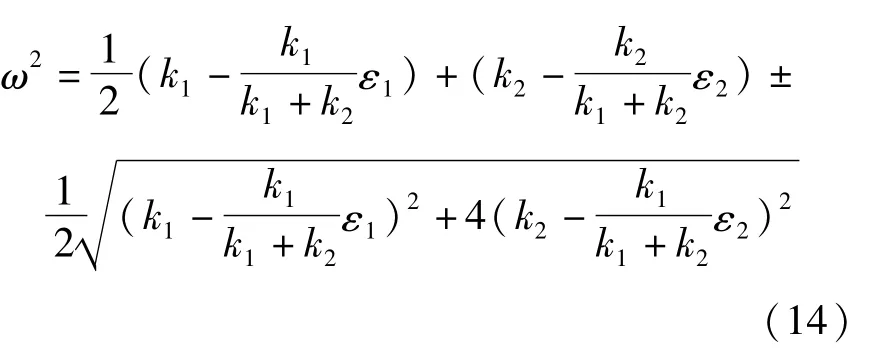
该公式不同于文献［8］中给出的等效模态频率公式：

其中：

在下一节中将通过数值方法来比较两种计算分段光滑线性系统模态频率的公式的精度.

2.3 非线性模态曲线斜率的确定

系统的模态运动在位形空间（x1-x2）中是弹簧刚度的函数，从方程（9）中可以得到系统在初始位移处模态运动的曲线：

（a）当两振子在图2第一区域时，K1＝k1-ε1，K2＝k2-ε2，代入系统模态曲线斜率公式得：

（b）当两振子在图2第二区域时，K1＝k1，K2＝k2-ε2，模态曲线斜率公式为：

（c）当两振子在图2第三区域时，K1＝k1，K2＝k2-ε2，代入系统模态曲线斜率公式得：

（d）当两振子在图2第四区域时，K1＝k1-ε1，K2＝k2，模态曲线斜率公式为：

各个区域的模态曲线的斜率都是一正一负成对出现，在取模态斜率时，要根据其在不同区域的其模态走势，来决定斜率的正负值，模态运动曲线满足方程

2.4 非线性模态的数值求解

对于给定系统，非线性模态是一种特殊的运动方式，且由初始位移决定.对于保守系统，如果系统的初始速度为零，则由方程（6）确定满足非线性模态运动的初始位移是关键.在位形空间内，模态运动曲线连接能量曲线上的两个固定点（即拉伸或压缩的最大位移点），并且在两定点处，曲线斜率不变（即两振子的速度同时为零）.也就是说，上述两质点位移和速度需满足以下条件：i）两振子位移满足方程（6），即该位移点在能量曲线上；ii）两振子的速度均为零，或在i）中位移点的两侧其符号同时发生变化.

图3中实线表示的是非线性模态运动，而虚线所表示的一般运动曲线，其与能量曲线可以有多个交点，且在每个交点处，趋近交点和远离交点的斜率不同，所以两振子的速度不同时为零.由此可采用如下数值解法来求解非线性模态：

1）在能量曲线上取一个初始位移点，为求同相和反相模态，可以把3.1节的理论幅值作为初始位移点的预估值.对于多余模态，其初始位移点必定在能量曲线上同相和反相模态初始位移点的预估值之间；

2）选定初始位移点后，采用龙格库塔法求解方程（1），获取两振子的位移和速度.a）当所求位移和速度同时满足条件i）和ii）时，计算停止，两振子的位移曲线即为模态曲线；b）若位移满足i），而速度不满足ii）时，停止计算，说明所取的初始位移点不在模态运动的曲线上；c）若所求的位移点与选定的初始位移点的差值小于预设的误差，则计算停止，说明两振子完成了一个周期的运动，该运动曲线不满足条件，不是非线性模态运动曲线.

图3 位形空间中的非线性模态解和一般运动解.（a）同相模态的确定；（b）反相模态的确定Fig.3 The solutions of nonlinear normalmode and of othermotions.（a）The determination of the in-phasemodes；（b）The determination of the anti-phasemodes

3 非线性模态特性的分析

由于上节的分析是针对分段线性系统各个光滑段分别进行分析处理，其只是对于真实系统非线性模态的近似处理，其可为数值求解该系统非线性模态提供初值的估算方法.通过数值计算与理论结果的比较也可以帮助我们认识，在多大程度上近似理论分析可以用来对非线性模态特性进行估计.在本文下面的分析中系统参数将取如下值：m1＝1.0，m2＝1.0，k1＝1.0，k2＝1.8，E＝10.0.

3.1 同相模态

同相模态是指系统振子同步振动，两弹簧同时拉伸或同时压缩，且同时同向达到最大位移或通过分界点，两振子的运动在第Ⅰ和Ⅲ区域内（见图4）.如果模态曲线与x轴的夹角为45°，说明两振子的位移差是常数，两振子的速度相同，两弹簧的压缩比不变，加速度大小也不变.如果模态曲线在第Ⅰ区域的倾角大于45°，则表明：Δx2大于Δx1，m2的速度和加速度也比较大.如果模态曲线在第Ⅲ区域的倾角大于225°，则表明：Δx2的大于 x1，m2的负向速度和负向加速度也较大.反之亦成立.

图4 同相模态运动曲线，刚度值 k1＝1.0，k2＝1.8.虚线（ε1，ε2）＝（0.0，0.75），点划线（ε1，ε2）＝（0.45，0.75），实线（ε1，ε2）＝（0.75，0.75）Fig.4 The in-phase normalmode curves，the stiffness is k1＝1.0，k2＝1.8.where dash line is in the case of（ε1，ε2）＝（0.0，0.75），the dot-dash line（ε1，ε2）＝（0.45，0.75），and the line（ε1，ε2）＝（0.75，0.75）

但非线性模态曲线的形状由系统的刚度和间隙值决定，下面讨论 ε2＝0.75，而 ε1变化时，对应的同相模态曲线的变化情况.由图4可以看出：k1、k2和k2-ε2不变，能量曲线在Ⅰ和Ⅳ区域的形状仅由ε1决定，且随着ε1的增大而伸长.此时，模态曲线向右下方倾斜.由于能量曲线在Ⅱ和Ⅲ区域的形状不由ε1决定，随着ε1的增大，能量曲线的形状未发生变化，但模态曲线倾斜和弯曲发生变化，并偏离x2-x1＝0直线，表明非线性特征逐渐增强.

在图5中，实线为数值计算的模态曲线，红虚线为理论估算的模态曲线.当间隙（裂纹）诱导的刚度变化量小时，理论模态曲线和数值模态曲线基本重合（见图 5a，参数（k1，k2，ε1，ε2）＝（1.0，0.8，0.15，0.15））；而随着间隙诱导的刚度变化量大时，理论模态曲线和数值模态曲线走势虽然基本一致，但可以看出，数值模态曲线已不再是直线.表明此时非线性特征增强（见图 5b，参数（k1，k2，ε1，ε2）＝（1.0，1.8，0.3，0.75））.

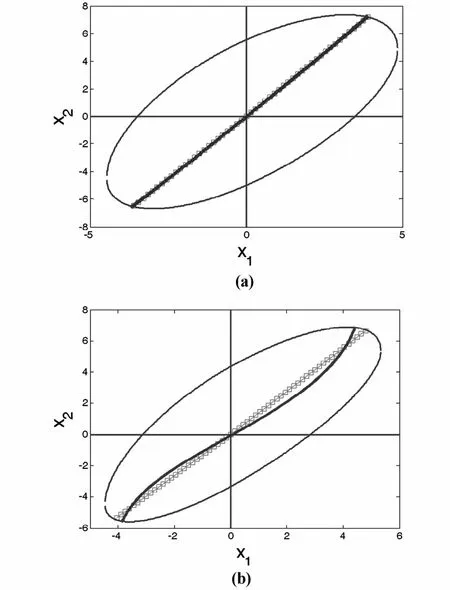
图5 同相模态运动曲线.虚线表示理论结果，实线为数值计算结果.Fig.5 The in-phase normalmode curve.The dash line is the theoretical one and the line is the numerical one.

表1给出了间隙诱导不同刚度变化量下，采用理论公式（14）计算系统同相模态频率与数值计算的同相模态频率的比较，可以看出：本文提出的理论计算模态频率，结果误差不超过2%，较文献［8］中采用的等效模态频率更为准确.表中还可以看出：数值确定的模态曲线的初始位移与理论预估的初始位移相差不大，后者可作为数值求解模态曲线的预估值.

表1 E＝10.0、k1＝1.0、k2＝1.8同相模态对应数值和理论结果Table 1 E＝10.0、k1＝1.0、k2＝1.8 The theoretical and numerical value about the in-phase normalmode

3.2 反相模态

在反相模态运动中，两振子运动的相位差为180o，即同时反向达到最大位移，交替出现一个弹簧拉伸、另一个弹簧压缩.图6为间隙诱导不同刚度变化量下的反相模态曲线图.可以看出：只要εi，i＝1，2，不为零，反相模态曲线就不经过原点.但间隙诱导的刚度变化量值越小，反相模态曲线越靠近原点.另外，反相模态曲线经过第Ⅰ、Ⅱ和Ⅳ区域，在第Ⅱ和Ⅳ区域，两弹簧出现一拉、一压的情形，而在第一区域，两弹簧同时处在拉伸状态，但是两振子的运动方向相反.

图6 反相模态运动曲线，刚度值 k1＝1.0，k2＝1.8.虚线（ε1，ε2）＝（0.0，0.75），点划线（ε1，ε2）＝（0.45，0.75），实线（ε1，ε2）＝（0.75，0.75）Fig.6 The anti-phase normalmode curve，the stiffness is k1＝1.0，k2＝1.8.where the dash line is in the case of（ε1，ε2）＝（0.0，0.75），the dot-dash line（ε1，ε2）＝（0.45，0.75）and the line（ε1，ε2）＝（0.75，0.75）

在图7中，实线为数值计算的模态曲线，虚线为理论估算的模态曲线.由于假设解的形式决定了理论模态曲线通过坐标原点，当间隙（裂纹）诱导的刚度变化量小时，理论模态曲线和数值模态曲线相接近（见图7a，参数（k1，k2，ε1，ε2）＝（1.0，0.8，0.15，0.15））；而随着间隙诱导的刚度变化量增大时，虽然理论模态曲线和数值模态曲线的斜率基本一致，但可以看出，数值模态曲线偏离原点的距离也在增大，其原因主要由于系统的非对称性所致（见图7b，参数（k1，k2，ε1，ε2）＝（1.0，1.8，0.3，0.75））.

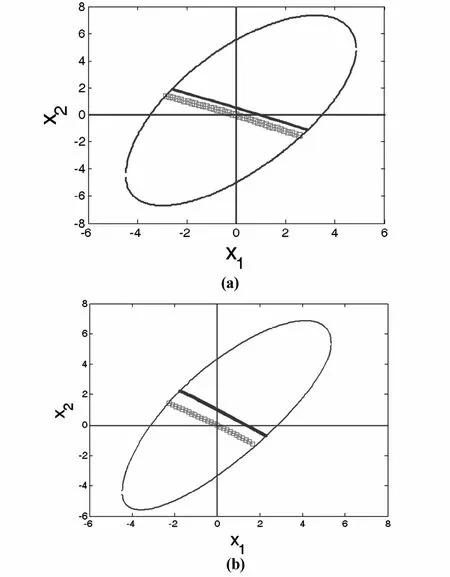
图7 反相模态运动曲线.虚线表示理论结果，实线为数值计算结果.Fig.7 The anti-phase normalmode curve.The dash line is the theoretical one and the line is the numerical one.

表2给出了间隙诱导不同刚度变化量下，采用理论公式（14）计算系统反相模态频率与数值计算的反相模态频率的比较，可以看出：本文提出的理论计算模态频率较文献［8］中采用的等效模态频率更为准确.表中还可以看出：随着间隙诱导刚度变化量的增大，理论预估的初始位移与数值确定的模态曲线的初始位移相差越来越大，说明理论假设的反相模态曲线的解有待于进一步改进.

表 2 E＝10.0、k1＝1.0、k2＝1.8反相模态对应数值和理论结果Table 2 E＝10.0、k1＝1.0、k2＝1.8 The theoretical and numerical value about the anti-phase normalmode

图8 非线性系统的多余模态运动曲线及其对应的初始坐标，其中：参数（k1，k2，ε1，ε2）＝（1.0，1.8，0.3，0.75）.初始位移分别为：（a）（x0，y0）＝（-2.7000，-5.3573）；（b）（x0，y0）＝（-1.3250，-4.5087）；（c）（x0，y0）＝（0.4250，-2.8978）；（d）（x0，y0）＝（4.6000，2.9023）；（e）（x0，y0）＝（5.3000，4.8673）Fig.8 The abundant normalmode curves and the corresponding initial values.The parameters（k1，k2，ε1，ε2）＝（1.0，1.8，0.3，0.75）.The initial values are（a）（x0，y0）＝（-2.7000，-5.3573）；（b）（x0，y0）＝（-1.3250，-4.5087）；（c）（x0，y0）＝（0.4250，-2.8978）；（d）（x0，y0）＝（4.6000，2.9023）；（e）（x0，y0）＝（5.3000，4.8673），respectively

3.3 多余模态

非线性系统的模态数会大于系统的自由度数.非线性模态除去与其线性化系统对应的模态外的其它模态，称为多余模态.多余模态往往是由于非线性系统满足内共振条件时产生的，其表现为基本（同相和反相）模态之间的能量转换运动.

由于非线性多余模态的形式和数量事先是未知的，本文采用数值方法，通过在能量曲线上搜索，来寻找满足模态运动条件的多余模态的初值.图8给出了在给定系统参数值时，找到的五个多余模态曲线和其相对应的初值点坐标.可以看出：多余模态分别呈现Z型和S型.Z型模态曲线的上下两段曲线与反相模态曲线方向相同，包含有反相模态运动的信息，而连接上下两段曲线的中间曲线与同相模态曲线方向相同，含有同相模态的信息.S型模态曲线上下两段曲线与同相模态曲线方向相同，包含同相模态运动信息，而连接上下两段曲线的中间曲线与反相模态曲线方向相同，含有反相模态的信息.由此可知：多余模态确实是由同相模态运动和反相模态运动组合而成的.

4 结论

本文针对含间隙的二自由度弹簧-质量系统模型的非线性模态开展了研究.首先，通过假设模态解的形式，求解出了分段光滑系统的同相模态和反相模态解.并提出了一种加权估算系统同相和反相模态频率的理论公式.通过数值求解系统的同相和反相模态，证实：本文所提的预估系统模态频率的公式较之前文献中的等价模态频率的计算公式更为准确.另外，理论模态解可以作为数值求解方法的预估初值.由于非线性系统的模态数会高于系统的自由度数，本文根据系统模态满足的条件，并采用数值方法，通过对能量曲线上点的搜索，发现了系统的五个多余模态.这五个多余模态均表现为同相和反相模态的内共振运动行为.

虽然，理论分析的结果在一定程度上（间隙诱导的刚度变化量小时）可以反映该非光滑系统的同相和反相模态，但随着间隙诱导的刚度变化量增大时，理论预测的误差越来越大，因此，有待于进一步改进理论假设解函数的形式，以便更准确地预测系统的同相和反相模态，甚至是多余模态，对此需要进一步研究.

1 Rosenberg R M.On normal vibrations of a general class of nonlinear dual-mode systems.Journal of Applied Mechanics，1962，29：7～14

2 Rosenberg RM.Nonsimilar normalmode vibrations of nonlinear systems having two degrees of freedom.Journal of Applied Mechanics，1964，31：283～290

3 Lacarbonara W，Rega G，Nayfeh A H.Resonant non-linear normal modes.Part I：analytical treatment for structural one-dimensional systems.International Journal of Non-Linear Mechanics，2003，38：851～872

4 Zhang Y M，Lu Q S.On the superposition of Shaw’s nonlinear normalmode.Acta Mechanica Sinica，2002，34：143～146

5 Xu J，Lu Q S，Huang K L.Nonlinear normalmodes and their superposition in a two degree of freedom asymmetric system with cubic nonlinearities.Applied Mathematics and Mechanics，1998，19：1077～1086

6 Slater JC.A numericalmethod for determining nonlinear normalmodes.Nonlinear Dynamics，1996，10：19～30

7 Chen S，Shaw SW.Normalmodes for piecewise linear vibratory systems.Nonlinear Dynamics，1996，10：135～164

8 Vestroni F，Luongo A，Paolone A.A perturbation method for evaluating nonlinear normalmodes of a piecewise linear two-degrees-of-freedom system.Nonlinear Dynamics，2008，54：379～393

9 Srinil N，Rega G.Two-to-one resonantmulti-modal dynamics of horizontal／inclied cables.Part II：Internal resonance activation，reduced order models and nonlinear normal modes.Nonlinear Dynamics，2007，48：253～274

10 Rand R H，Pak CH，Vakakis A F.Bifurcation of nonlinear normalmodes in a class of two degree of freedom systems.Acta Mechanica，1992，3：129～145

11 Casini P，Vestroni F.Characterization of bifurcating nonlinear normal modes in piecewise linear mechanical systems. International Journal on Non-Linear Mechanics，2011，46：142～150

12 Butcher E A.Clearance effects on bilinear normalmode frequencies.Journal of Sound and Vibration，1999，224（2）：305～328

13 Jiang D，Pierre C，Shaw SW.Large-amplitude nonlinear normalmodes of piecewise linear systems.Journalof Sound and Vibration，2004，272：868～891

14 Giannini O，Casini P，Vestroni F.Experimental evidence of bifurcating nonlinear normal modes in piecewise linear systems.Nonlinear Dynamics，2011，63：655～666

15 郭其威，吴松，刘芳，赵阳东等.航天器模态分析-试验体系工程实践研究.动力学与控制学报，2014，12（3）：274～278（Guo QW，Wu S，Liu F，et al.Research on engineering practice of modal analysis-test of spacecraft.Journal of Dynamics and Control，2014，12（3）：274～278（in Chinese） ）