分数阶混沌系统的主动滑模同步*

仲启龙 邵永晖 郑永爱

（扬州大学信息工程学院，扬州 225127）

引言

尽管分数阶微积分理论有300多年的历史，但因长时间没有实际的应用背景而发展缓慢.自从1983年Mandelbort指出自然界及许多科学技术领域中存在大量的分数维事实，分数阶微积分才取得了很大的进展.另一方面，OGY控制方法［1］和 PC同步方法［2，3］的提出，使整数阶混沌系统的控制和同步有了突破性的发展.然而由于分数阶混沌系统的同步在保密通信、信号处理和系统控制等领域比整数阶混沌系统拥有更突出的应用前景和发展前途，因此近年来，分数阶混沌系统的研究受到很多学者的重视，有了很多的成果.分数阶混沌系统同步的方法相继被提出，例如，自适应同步［4］、耦合同步［5］、主动控制同步［6］、滑模控制同步［7-11］、鲁棒观测器同步［12-13］等.近来，一些学者结合多种控制方法实现了分数阶混沌系统的同步.结合自适应控制和模糊滑模控制，文献［14］实现了分数阶混沌系统同步；文献［15］利用主动滑模变结构控制实现不同维分数阶混沌系统的同步；文献［16］设计整数阶滑模面，利用单向耦合特性实现分数阶混沌系统同步.文献［17］利用分数阶微积分设计滑模面，实现不同维的分数阶混沌系统同步，但该文中需要对每一维状态分量分别设计滑模面.

针对文献［17］中需要对每一维状态分量分别设计滑模面，本文提出一个新的同步分数阶混沌系统的主动滑模控制方法，该方法首先用分数阶积分对所有维状态分量设计一个滑模面，分数阶混沌系统在该滑模面上稳定.然后采用极点配置的方法获得主动滑模控制器中的增益矩阵.通过仿真实验验证了该方法的可行性与有效性.

1 分数阶微积分

分数阶微分的定义有多种，其中应用较多的是Riemann-Liouville（R-L）分数阶微分和Caputo分数阶微分［18］.在理论研究中应用较多的是R-L定义.由于Caputo的分数阶微分定义更容易给出分数阶微分方程的初值条件，因而在工程中应用较广.本文采用R-L积分算子以及Caputo定义.

定义1Riemann-Liouville分数阶积分算子这里 q＞0，f：R→R，Γ（·）为伽玛函数，且

定义2Caputo分数阶微积分定义

这里 n-1≤q≤n∈N，f（t）为在 t＞0时在［0，t］上有n+1阶连续有界可导的函数.

文献［19］研究并给出了判断分数阶线性系统稳定性的充要条件.

引理1考虑自治系统如下

其中，

如果有

1）当且仅当对矩阵A的任意特征值｜arg（eig（A））｜＞απ／2恒成立，则系统是渐近稳定的，

2）当且仅当对矩阵A的任意特征值｜arg（eig（A））｜＞απ／2恒成立，则系统是稳定的，

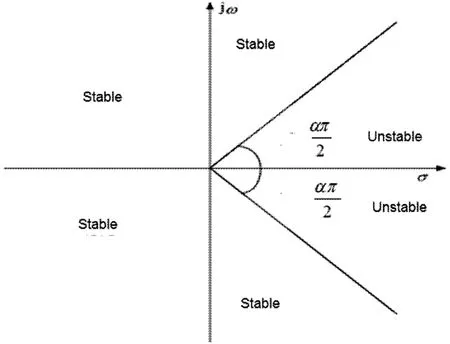
图1 阶线性系统的稳定性区域Fig.1 Stability region of linear system with order

α阶线性系统的稳定区域如图1所示，对于分数阶非线性系统如果其在平衡点处的Jacobian矩阵的所有特征值都在稳定区域内，则该平衡点为稳定的平衡点.

2 分数阶混沌系统的主动滑模同步

系统形式如下：

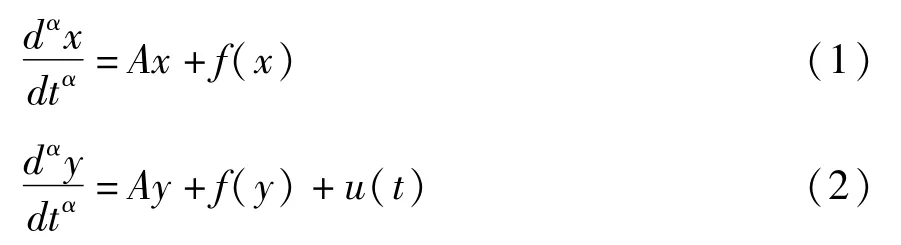
其中 x＝［x1，x2，…，xn］T为驱动系统输入，y＝［y1，y2，…，yn］T为响应系统输入，A为系统线性项系数矩阵，f（·）为系统的非线性项，u（t）＝［u1，u2，…，un］T为系统控制输入项.

设响应系统与驱动系统之间的状态误差.

则

其中 e＝［e1，e2，…，en］T.

我们只要选取合适的控制器u（t），使得，即驱动系统与响应系统同步.

控制器设计如下：

其中 k＝［k1，k2，k3］T∈R，

误差系统方程为

设计滑模面为

其中 c＝［c1，c2，c3］∈R，则

当分数阶系统在滑模面运动时，滑模面应满足

将误差系统（7）代入（11）得

化简上式可得等效控制

将系统（13）代入误差系统（7）得

其中B＝k，K＝（ck）-1cA

利用极点配置［20］的方法使得系统矩阵（ABK）的特征值为｛p1，p2，…，pn｝，误差系统配置在稳定范围内.

其中｛γ0，γ1，…，γn-1｝是系数矩阵 A的特征多项式的系数，即

｛β0，β1，…，βn-1｝是系数矩阵（A-BK）的特征多项式的系数，即

矩阵

然后设计滑模到达控制律

式中 μ，τ＞0，sgn（·）为符号函数.将（9）式代入（19）式得

将（7）式代入得

化简

定理1从任意初始条件出发，误差系统（7）始终满足 ˙s＝-μsgn（s）-τs的滑模到达条件，则误差系统（7）能在有限时间内到达趋近滑模面（8）.

证明： 考虑如下的Lyapunov指数

这里 μmin＝min｛μi｝，τmin＝min｛τi｝，i＝1，2，…，n.因此，对所有μmin＞0和τmin＞0，系统的轨迹在控制律（19）的作用下达到滑动模态.证毕.

当误差动态系统到达滑模面时有

由极点配置定理可控制系统的特征值｛p1，p2，…，pn｝满足｜arg（pi）｜＞，i＝1，2，…，n.所以系统渐进稳定，所以驱动系统与响应系统同步.

3 仿真示例

以分数阶Lorenz混沌系统为例进行仿真，以下分别为响应系统和驱动系统.

其中 a＝0.96，a＝10，b＝28，c＝8／3.

系统误差方程为

设计控制器如下

因此误差系统（27）可以表示成

滑模面定义为：

滑模面应满足以下条件

化简（32）式可得等效控制

然后将（33）式代入（29）式的系统的误差方程得

化简得

利用极点配置的方法，设定参数 c1，c2，c3与k1，k2，k3使得｜arg（pi）｜＞απ／2，i＝1，2，3，其中 pi为误差系统参数矩阵的特征值.特征值设计如下：p1＝-0.0063，p2＝-0.0018+2.0001i，p3＝-0.0018-2.0001i，k1＝k2＝k3＝1，则 c1＝1.5475，c3＝-0.0379，˙s＝-0.2sgn（s）-20s.

初值（x10，x20，x30）T＝（2，-1.5）T，（y10，y20，y30）T＝（5，-3，-2）T，时间步长 h＝0.01，在 t＝20s时加入控制.

图2 同步误差与控制变量状态曲Fig.2 States trajectories of the synchronization error and state variables

用Matlab对驱动系统与响应系统进行仿真，图2为系统同步误差与控制变量状态曲线图.从图中可以看出，当未加控制变量时，系统误差始终在变化；当t＝20s时加入控制变量后，驱动系统与响应系统很快趋于同步.

4 结论

基于分数阶混沌系统的同步问题，本文提出同步分数阶主动滑模控制方法，首先设计分数阶积分滑模面，然后利用极点配置法处理控制器增益矩阵，控制系统达到同步，并且进行了稳定性分析证明.以分数阶Lorenz为例进行仿真，仿真结果验证了该方法的可行性与有效性.

1 Ott E，Grebogi C，Yorke JA.Controlling chaos.Physics Review Letters，1990，64：1196～1199

2 Carroll T L，Pecora L M.Synchronizing chaotic circuits.IEEE Transactions of Circuits System I，1991，38：453～456

3 Pcora L M，Carroll T L.Synchronization in chaotic systems.Physics Review Letters，1990，64（8）：821～824

4 Yang Q G，Zeng CB.Chaos in fractional conjugate Lorenz system and its scaling attractors.Communications in Nonlinear Science and Numerical Simulation，2010：4041～4051

5 Zhu H，Zhou S B，He Z S.Chaos synchronization of the fractional-order Chen’s system.Chaos，Solitons and Fractals，2009，41：2733～2740

6 Radwan A G，Moaddy K，Salama K N，et al.Control and switching synchronization of fractional order chaotic systems using active control technique.Journal of Advanced Research，2013，13（1）：125～132

7 刘丁，闫晓妹.基于滑模控制实现分数阶混沌系统的投影同步.物理学报，2009，58（6）3747～06（Liu D，Yan X M.Projective synchronization of fractional2order chaotic systems based on sliding mode control.Acta Physica Sinica，2009，58（6）：3747～06（in Chinese））

8 Yin C，Dadras S，Zhong SM，et al.Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach.Applied Mathematical Modelling，2013，37：2469～2483

9 Chen N，Wang N Z.Synchronization of chaotic systems via slidingmode controlwith fractional approach law.In：Con-trol and Decision Conference（CCDC），2011：1304～1307

10 曹鹤飞，张若洵.基于滑模控制的分数阶混沌系统的自适应同步.物理学报，2011，60（5）：050510（Cao H F，Zhang R X.Adaptive synchronization of fractional-order chaotic system via slidingmode control.Acta Physica Sinica，2011，60（5）：050510（in Chinese））

11 孙宁，张化光，王智良.基于分数阶滑模面控制的分数阶超混沌系统的投影同步.物理学报，2011，60（5）：050511（Sun N，Zhang H G，Wang Z L.Fractional sliding mode surface controller for projective synchronization of fractional hyperchaotic systems. Acta Physica Sinica，2011，60（5）：050511（in Chinese））

12 Li C L，Sua K L，Tong Y N，et al.Robust synchronization for a class of fractional-order chaotic and hyperchaotic systems.Optik-International Journal for Light and Electron，2013，124（18）：3242～3245

13 Gammoudi IEl，Feki M.Synchronization of integer order and fractional order Chua’s systems using robust observer.Communication in Nonlinear Science and Numerical Simulation，2013，18：625～638

14 Lin T C，Lee T Y.Chaos synchronization of uncertain fractional-order chaotic systemswith time delay based on adaptive fuzzy sliding mode control.IEEE Transactions on Fuzzy Systems，2011，19（4）：623～635

15 Bai J，Yu Y G.The synchronization of fractional order chaotic systems with different dimensions through sliding mode control.International Workshop on Chaos-Fractals Theories and Applications，2011，4：239～243

16 Razminia A，Baleanu D.Complete synchronization of commensurate fractional order chaotic systems using sliding mode control.Mechatronics，2013，23（7）：873～879

17 黄丽莲，齐雪.基于自适应滑模控制的不同维分数阶混沌系统的同步.物理学报，2013，62（8）：080507（Huang L L，Qi X.The synchronization of fractional order chaotic sysemswith differentorders based on adaptive slidingmode control.Acta Physica Sinica，2013，62（8）：080507（in Chinese））

18 Podlubny I.Fractional differential equations.New York：San Diego Academic Press，1999

19 Ahmed E，El-Sayed AM A，El-Saka H A A.Equilibrium points，stability and numerical solutions of fractional-order predator-prey and rabies models.Journal of Mathematical Analysis and Applications，2007，325（1）：542～553

20 Naceri A，Mansouri N，Charef A.Prediction-based feedback control of fractional order system.IEEE，2008：908～912