基于压缩感知的一类带噪声电气系统的故障诊断

叶北林 梁凯豪 熊平原

（1.从化市职业技术学校，广州 510920;2.仲恺农业工程学院计算科学学院，广州 510225;3.仲恺农业工程学院机电学院，广州 510225）

复杂的电力系统往往会包含很多子系统，以建筑上的电力系统为例，它包含了照明子系统、供配电子系统、动力设备子系统、办公及管理自动化子系统等[1]，不同子系统之间的相互作用增加了整个系统的复杂性。

目前，出现的故障智能诊断方法主要有神经网络、支持向量机（SVM）、高斯过程分类器等方法[2-4]，这些方法极大提高了故障的诊断效率。龚瑞昆等[2]针对电力变压器故障，先对量子神经网络进行局部融合诊断，再将各局部诊断信息引入决策融合网络进行全局融合，提出了基于量子神经网络信息融合的故障诊断方法。尹金良等[3]围绕变压器故障诊断问题，构建了基于拉普拉斯近似方法的高斯过程分类器，分类器中均值函数采用常函数，协方差函数采用全平方指数函数，而似然函数采用误差函数。崔江等[4]针对模拟电路的故障诊断问题，先对电路故障样本进行训练建立支持向量机模型，并根据训练参数构建故障字典；然后对未知样本进行测试，判断故障类型。但这些方法也存在一定的诊断误差，运用量子神经网络的故障误诊率为2.2%，采用高斯过程分类器的误诊率为8.3%，而基于SVM 的故障误诊率为2.4%。张龙和陈宸等根据Candes、Donoho和Tao 等提出的压缩感知理论建立了一种在建筑电气系统上的故障诊断方法，该方法在故障诊断准确率上取得了较好效果[1]，但是该方法没有考虑到在带干扰的电力系统中的故障诊断情况以及算法的鲁棒性。本文主要考虑在带干扰的电力系统中，如何准确地诊断故障的位置以及诊断算法的鲁棒性。将故障诊断问题看作是稀疏故障信号和故障类型的一种对应关系，并构建测量矩阵和测量相应位置的电阻，从而恢复故障信号，判断故障类型。

1 基于压缩感知的电气故障诊断

1.1 压缩感知故障诊断原理

电气系统的故障诊断实质上是从故障信息集到故障类型集的一种映射关系，即由观测到的信息判断故障的状态类型[5]。假设故障信息集Y包含了m个故障信息值，即故障信息集Y中的任意一个元素y，有y∈Rm。设故障类型集只有k个元素，每个 元素表示一种故障类型。

电气系统故障诊断过程可以看作一个分类过程，根据观测到的信息y，利用故障诊断算法输出故障类型，再根据故障类型，判断故障发生的位置。

1.2 测量矩阵的构建

利用压缩感知方法进行电气系统故障分类时，先要构建压缩感知问题的测量矩阵。从第i类故障中随机抽取ni(i= 1,2,… ,k)个训练样本，每个训练样本都测量其m个故障信息值，将第i类故障的训练样本组合到一起，则得到第i类故障的训练样本矩阵[1]

式中，∈Rm×1为第i类故障的第j个训练样本，的m个分量为样本所对应的m个故障信息值，为第i类故障的训练样本矩阵。

将所有k个类别的训练样本矩阵组合起来，则构建出初始测量矩阵

式中，aij∈R，而Ai,j∈Rm×1。

1.3 带噪声故障诊断的l0 范数最小化问题

设测试样本属于第i类故障，则测试样本的故障信息向量y∈Rm可以表示为完备化后的第i类故障训练样本矩阵的线性组合[5]，即

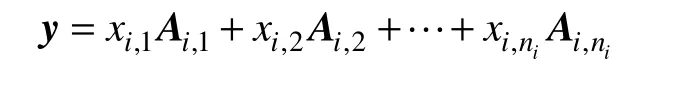
式中，xi,j为权重系数。当测试样本的故障信息向量y的故障类型未知时，则y可以通过测量矩阵A表示为

式中，x=(x1,x2,…,xk)T∈RN×1，xi= (xi,1,xi,2,…,xi,ni)T∈Rni×1。此时，如果给定的y属于第i类故障，则有

此时，称x为ni稀疏向量，即Card(supp(x) ) ≤ni，其中supp(x)表示向量x的支撑集，Card(supp(x))则表示支撑集的元素个数，同时，可把x看作y的稀疏向量分解，即求式（4）中，x的l0范数最小值

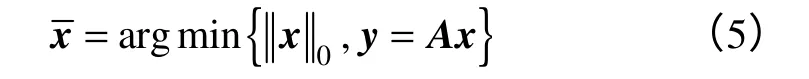
在实际的测试当中，测试样本的故障信息向量y往往会受到干扰，而出现测量误差。我们称这些干扰为噪音。则式（6）中的测试样本的故障信息向量y应该表示为

要确定测试样本的故障类型，只要在式（6）中，对y做稀疏向量分解，求x的l0范数最小值，则可得到稀疏向量x，根据稀疏向量x中，非零分量所在的位置，则可以确定测试样本的类型。带噪声的l0范数最小化问题为

但不幸的是，式（7）的l0范数最小化问题为NP-hard问题[6]，其计算量呈现阶乘级数增长，当A的行数和列数较大时，普通计算机也难以求解该问题。因此，必须通过其他算法求解式（7）的l0范数最小化问题。

2 l0 最小化问题的求解

2.1 l0 问题与l1 问题解的一致性

由于式（7）的l0范数最小化问题是是一个NP-hard 问题，一个自然的想法就是用l1范数最小化问题来求解l0问题，即求解

但是，这里需要解决l0问题与l1问题的解是否一致的问题。Candes，Romberg 和Tao[7]证明了在测量矩阵A满足RIP 条件（restricted isometry property）下，l0问题与l1问题的解是一致的，即用l1最小化能用y准确恢复x。

2.2 故障测量矩阵的RIP 条件

我们说测量矩阵A满足s-阶RIP 条件，如果存在常数δs∈ [ 0,1)，使得

Candes 和Tao 等证明了[8]，若测量矩阵A满足2s阶RIP 条件，且RIP 常数则对任意的s稀疏向量x，即 Card ( supp(x) )≤s，均有l0问题与l1问题的解是一致的。但是，对于给定的一个测量矩阵A，难以从理论上证明其满足RIP 条件，当A的行数和列数较多时也不容易在计算机上快速验证其RIP 条件。

2.3 测量矩阵的高斯分布检验

当测量矩阵A为高斯随机矩阵时，则A满足RIP 条件δs≤δ的概率非常高。因此，将验证A的RIP 条件δs≤δ改为验证A的元素服从高斯分布。这里采用分布拟合检验方法验证A的元素服从高斯分布[9]，检验过程如下：

1）建立假设检验H0：aij服从高斯分布，备择假设H1：aij不服从高斯分布。

2）用M- 1个点t i(i= 1,2,…,M-1)将( -∞,+∞)分为M个互不相交的子区间(t i,ti+1]。用vi表示观测值ai j(i∈ [m] ,j∈ [N])落入区间(t i,ti+1]的个数，这个个数又称为组频数。记pi为总体落入区间的概率，即为标准高斯分布的密度函数。构造检验统计量

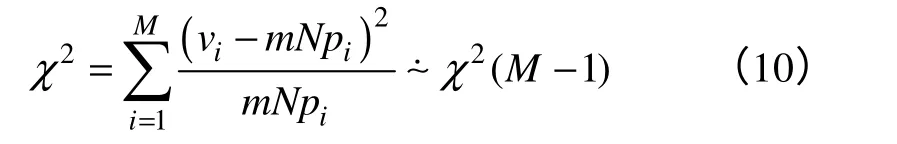
3）对于给定的显著性水平α，查χ2分布表，找临界值χα2(M- 1)，使得

得到拒绝域(χα2(M- 1),+∞)。

4）根据ai j(i∈ [m] ,j∈ [N])，计算检验统计量χ2，若χ2位于拒绝域之外，则接收原假设，拒绝备择假设，认为aij服从高斯分布；否则，认为aij不服从高斯分布。

若测量矩阵A通过了高斯分布拟合检验，则可以用算法来求解l1问题（8）；否则，需要对测量矩阵A重新调整，重新构建。

2.4 IRLS 算法

用Daubechies I 和Devore R 等提出的IRLS (iteratively reweighted least squares minimization)算法对l1问题（8）进行求解[10]。求解l1问题（8）的IRLS 算法为

IRLS 算法 IRLS( y ,e) 输入：测量矩阵A，测试向量y ，噪声模拟值e 输出：稀疏向量x 初始 化： w0=(1 ,…,1) ,ε 0=1.迭代：Dn=diag (1 w1n ,1 w2n ,…,1 wNn ),x n + 1 =Dn AT ( ADn AT ) -1( y -e ),εw nn j+ + 1 1 = = m ■■■(i nx nj■■■■ +ε 1 n ),2 r+( ε xn n2+ N+1 1 )■■■K-12+1.■■■■,迭代停止条件： ε n= 0，或迭代次数n 大于某个给定的值。

IRLS 算法中，r(xn+1)K+1表示将向量xn+1的各个分量取绝对值，并从大到小排列，取第K+ 1个位置的分量，即r(xn+1)K+1为xn+1各分量中第K+ 1个绝对值最大的分量。

3 故障诊断实验及结果分析

3.1 电气故障模拟实验

采用建筑电气系统测试平台MA2067 进行试验。该平台能够模拟建筑电气系统的运行及故障发生机制，它包含了弱电系统和强电系统两部分，其中强电系统是该实验平台的主体[11-12]。该实验平台通过故障设置面板的22 个开关模拟22 个故障位置的是否存在故障。这22 个位置的故障可以分为四大类阻值故障，分别为线路阻抗故障、连续性故障、接地电阻异常、绝缘电阻过小[13]。若将正常作为一类诊断状态，则一共有五类诊断状态。不同故障状态对应不同的故障位置，根据诊断的故障状态类型就可以判断故障发生的位置[14]。在实验中，采集实验平台10 个不同测试位置的电阻值组成故障信息 向量y，即y∈R10，10 个故障测试位置见表1。

在五类故障诊断状态中，对每类故障诊断状态分别随机地收集15 组样本数据，每组样本数据都包含了10 个不同故障位置的电阻值，计算其均值和标准差，数据见表1。将这75 组数据组合起来，则得到初始测量矩阵，将的每一行标准化，则得到完备测量矩阵A∈R10×75。

表1 实验平台测试故障位置

将( -∞,+∞)分为10 个互不相交的子区间，由分 布拟合检验，在显著性水平α= 0.05下，算得χ2= 3.17小于χ02.05(10) = 3.940。因此，可认为测量矩阵A为高斯随机矩阵。

3.2 结果分析

为了检验在第1 节中所建立的方法的有效性，这里选择第2 类故障诊断状态进行检验，设定其原始故障信号x，此时测定其10 个不同故障位置的故障信息值（电阻值）

将其标准化后分析根据IRLS 算法是否能够由y准确恢复故障信号x，若x可以准确恢复，则根据故障信号x可以判断故障类型。需要注意的是，由于在测试过程中，故障信息值y不可避免会存在误差e（这里又称噪声），这里不妨假设ej～N(0,0.1)。 因此，关键的问题是，由y恢复出来的故障信号x~ 与设定的故障信号x是否会很大差异。利用Matlab 实现IRLS 算法，结果如图1所示。图1中上图为设定的故障信号，而下图为恢复出来的故障信号。

由图1可知，恢复出来的故障信号和设定的故障信号基本一致。由于恢复出来的故障信号的非负分量分布在第2 类故障的位置，与设定的故障类型一致。此实验说明了故障诊断模型（7）的有效性。

图1 故障信号

随机选择一种故障类型，设定故障信号，测定相应位置的电阻值并加入高斯噪声，用算法恢复故障信号，诊断故障类型。在200 次随机试验中，有196 次识别准确，故障识别率为98%。而在无噪声的情况下，采用神经网络的故障识别率为97.78%，用SVM 的故障识别率为97.6%。

图2为恢复的故障信号和设定的故障信号两者之间随着迭代次数的增加，其误差的变化。由图2可知，经过3 次迭代之后，恢复的故障信号能够较好拟合实际故障信号，两者误差稳定在1%。而且，算法没有出现因为误差叠加而失控的情况。

图2 迭代误差

4 结论

本文针对带噪声的故障识别问题进行研究，在验证实验当中，算法只需要经过3 次迭代则能够恢复故障信号，而且恢复出来的故障信号和原来的故障信号一致，这说明利用压缩感知和IRLS 算法进行电气系统的故障诊断具有诊断效率较高，诊断准确的特点。通过多次实验计算可知，利用压缩感知方法的故障识别率约为98%，而利用支持向量机对电气系统进行故障诊断的故障识别率为97.6%[15-16]，比支持向量机的故障识别率高。另外，故障识别率的高低与测量矩阵的构建有关，测量矩阵如何影响识别率的问题，我们将进一步研究。

[1] 张龙,陈宸,韩宁,等.压缩感知理论中的建筑电气系统故障诊断[J].智能系统学报,2014,9(2): 204-209.

[2] 龚瑞昆,马亮,赵延军,等.基于量子神经网络信息融合的变压器故障诊断[J].电力系统保护与控制,2011,39(23): 79-84,88.

[3] 尹金良,朱永利,俞国勤,等.基于高斯过程分类器的变压器故障诊断[J].电工技术学报,2013,28(1): 158-164.

[4] 崔江,王友仁.基于支持向量机与最近邻分类器的模拟电路故障诊断新策略[J].仪器仪表学报,2010,31(1): 45-50.

[5] 韩安太,郭小华,廖忠,等.基于压缩感知理论的农 业害虫分类方法[J].农业工程学报,2011,27(6): 203-207.

[6] 许志强.压缩感知[J].中国科学:数学,2012(9): 865-877.

[7] Candes E J,Romberg J K,Tao T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics,2006,59(8): 1207-1223.

[8] Candes E J,Tao T.Decoding by linear programming[J].IEEE Transactions on Information Theory,2005,51(12): 4203-4215.

[9] 夏帆,倪青山.基于分布拟合的异方差检验[J].数量经济技术经济研究,2012(8): 114-123.

[10] Daubechies I,Devore R,Fornasier M A.Iteratively reweighted least squares minimization for sparse recovery[J].Communications on Pure and Applied Mathematics,2010,63(1): 1-38.

[11] 王英英,罗毅,涂光瑜,等.电力系统连锁故障的关联模型[J].电工技术学报,2012(2): 204-209.

[12] 郭金叶,佘维,李江林,等.一种基于EFPN 的电力系统故障诊断方法[J].电力系统保护与控制,2012(14): 10-15.

[13] 尹项根,陈庆前,王博,等.基于四层集合模型的复杂电力系统脆弱性评估体系[J].电工技术学报,2013,28(1): 225-233.

[14] 曾庆锋,何正友,杨健维.基于有色Petri 网的电力系统故障诊断模型研究[J].电力系统保护与控制,2010,38(14): 5-11,127.

[15] 刘友波,胡斌,刘俊勇,等.电力系统连锁故障分析理论与应用（一）——相关理论方法与应用[J].电力系统保护与控制,2013(9): 148-155.

[16] 曹玉苹,田学民.基于SVM 和Kalman 预测的非线性系统故障预报[J].控制与决策,2009,24(3): 477-480.