移相全桥动态模型及自适应模糊PID控制器设计
2015-05-27童文秀
童文秀 王 武
(福州大学,福州 350108)
随着DC/DC变换器在远距离传输、计算机、工业设备、军队、航天航空和其他领域中的应用越来越广泛,对DC/DC变换器的要求也越来越高。移相全桥DC-DC变换器利用变压器的漏感实现功率器件的零电压开通,大大降低了功率器件的开关损耗。移相全桥变换器具有高效,高功率密度,低电磁干扰的优点,已经成为目前大功率高频开关电源最常用的拓扑结构。但由于DC/DC变换器是强非线性系统,负载和扰动都能使变换器发生较大的变化。
随着离散控制算法和数字信号处理技术的发展,在电力电子控制装置中,数字控制几乎取代传统的模拟控制。传统PID控制是较早发展起来的控制策略之一,它具有算法简单、鲁棒性好、可靠性高的特点。因此,对DC/DC变换器这种强非线性系统,传统的PID控制越来越难以满足其不断提高的性能指标要求。自适应模糊控制是利用模糊数学的知识模仿人脑的思维方式,对模糊现象进行识别处理,然后给出精确的控制量,从而控制被控对象,能够实现控制器参数的自整定,解决了PID的固有问题。
1 移相全桥变换器动态模型建立与分析
移相全桥每个桥臂的两个开关管180°互补导通,两个桥臂导通之间相差一个相位,即为移相角。通过调节移相角的大小,来调节输出电压脉冲宽度,在变压器副边得到占空比可调的正负半周对称的交流方波电压,从而达到调节相应的输出电压的目的。文献[1]较为详细地介绍了移相全桥的工作原理。移相全桥变换器主电路如图1所示。
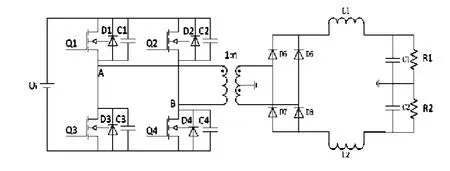
图1 移相全桥变换器主电路
通过建模,可以对变换器进行定性和定量分析。在诸多文献中,所推导及所涉及的移相全桥小信号模型皆基于BUCK 电路衍生而来。文献[2]较为详细地推导出移相全桥的小信号模型。通过抓住两者的不同点在于移相全桥具有固有的缺点,即存在占空比丢失,通过分析出扰动对占空比的影响,推导出传统移相全桥小信号模型等效电路,如图2(a)所示。

图2 移相全桥不同模型的等效电路
从图2(a)可得传统移相全桥的控制-输出传递函数为

式中,Rd= 4n2Lrf;f为开关频率;Lr为变压器漏感;Ui为输入电压;Io为输出电流;L为滤波电感, 1:n为原副边匝比。
然而传统小信号模型所忽略的参数,比如寄生参数、谐振电感和调制比等,皆是影响电路分析的关键因素,必然造成较大的误差。接下来本文将推导出一种基于先进动态模型的新移相全桥控制-输出传递函数。移相全桥动态模型等效电路如图2(b)所示。
其中等效电阻Req取决于变换器的所有损耗并影响变换器的效率。
直流和交流等效电路如图3所示。
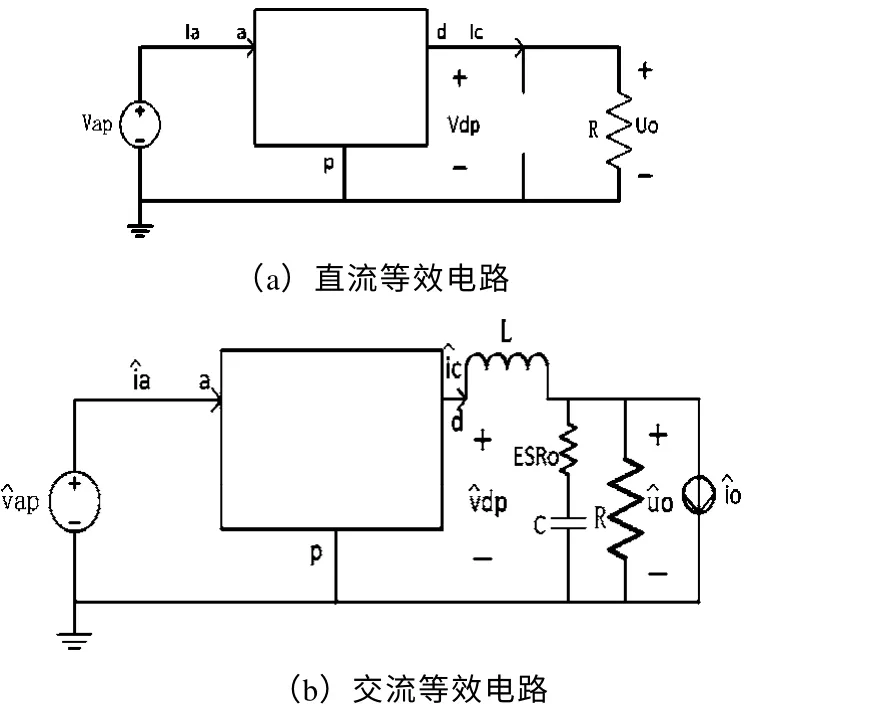
图3 直流和交流的等效电路
从图3(a)中,可得式(2)。
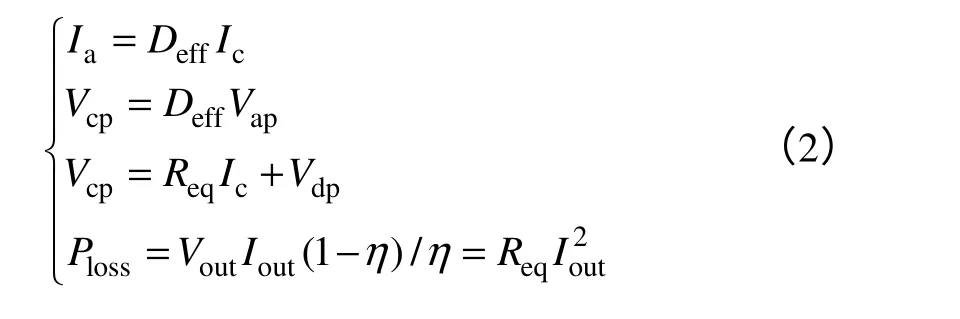
式中,Vap=nVin,Vdp=Vo,Ploss为变压器总的损耗,η为变换器效率,直流等效电路中电感等效电阻也包含在Req里。
从图3(b)中,可得式(3)。
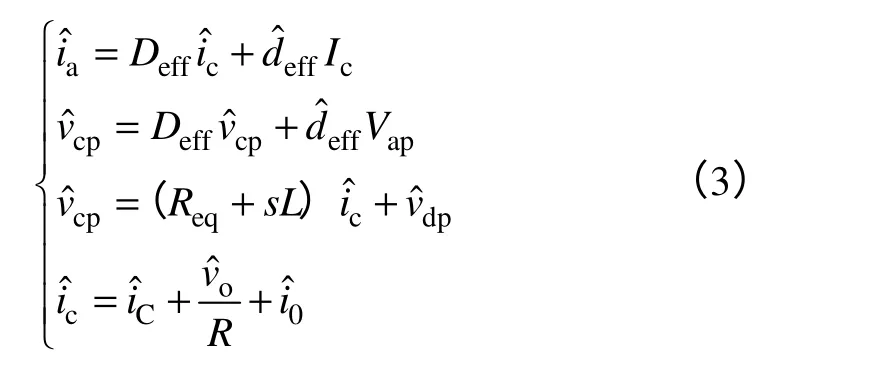
又因为

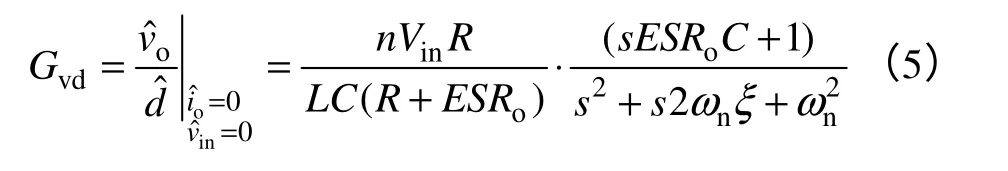
其中阻尼比ξ和自然频率ωn分别为

由上式可知,与传统的传递函数相比,多了一个零点。从式中也可看出,ESRo影响诸多因素,因此寄生参数不可省略。
2 自适应模糊PID 控制设计
1)传统PID 控制原理
传统PID控制是由比例、积分和微分环节构成,其参数是指比例系数Kp,积分系数Ki和微分系数Kd。它们对系统性能会产生不同的影响。文献[3]较为详细地分析了各系数的主要功能。
传统PID控制的控制规律为
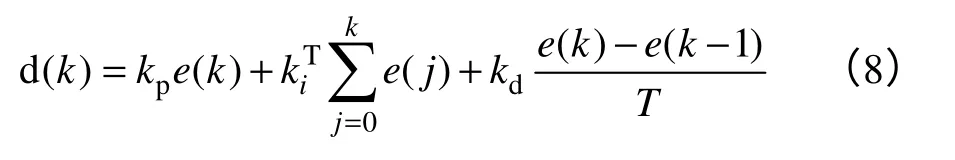
2)自适应模糊PID 控制原理
传统PID 控制器不具有在线整定参数的功能,因此不能满足在不同情况下系统对参数的自整定要求,难以保证其控制效果。自适应模糊PID 控制器通过在线识别被控过程参数来实时整定控制参数,其控制效果的好坏取决于辨识模型的精度,这对于复杂系统是非常困难的,不过操作人员仍有许多成功的经验对其进行控制,自然人们就想到将这些经验存入计算机,由计算机根据现场实际情况自动调整PID 参数,进而实时控制,于是就出现了自适应模糊PID 控制。
3)自适应模糊PID 控制系统结构
文献[4]提出的模糊PID控制,是直接对PID控制器的输出进行模糊增益控制。其控制对象只有一个,必造成比较大的误差。本文研究的自适应模糊PID控制器结构如图4所示,主要以输出电压Uo和参考电压Uref的误差变化率和误差,即ec和e作为控制器的输入参数,实时地修改Kp、Ki、Kd这3个控制参数,得到输出占空比d,从而使被控对象达到良好的动态特性。
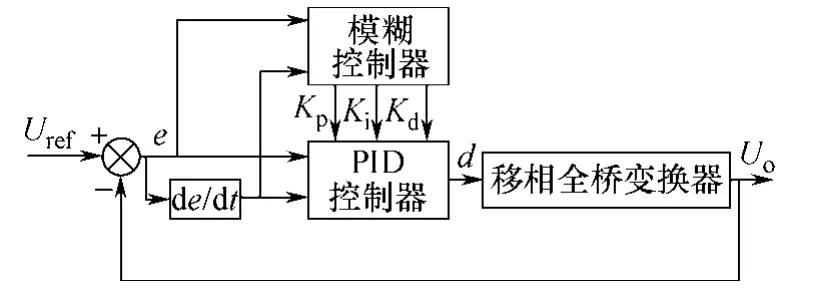
图4 自适应模糊PID 控制系统结构
4)确定模糊语言变量
设定e、ec、Kp、Ki、Kd的论域为:e、ec和Kp的论域为[-3,3],Ki的论域为[-0.3,0.3],Kd的论域为[-0.08,0.88]。我们选择简单的三角形隶属函数,每个模糊子集变量都包含有7 个元素,分别是PB(正大)、PM(正中)、PS(正小)、ZO(零)、NS(负小)、NM(负中)和NB(负大)。
5)模糊规则
Kp、Ki和Kd的模糊规则见表1。

表1 Kp、Ki 和Kd 的模糊规则

(c)Kd 模糊控制规则 e ec NB NM NS ZO PS PM PB NB PB PB PM PM PS ZO ZO NM PB PB PM PS PS ZO NS NS PM PM PM PS ZO NS NS ZO PM PM PS ZO NS NM NM PS PS PS ZO NS NS NM NM PM ZO ZO NM NM NM NB NB PB ZO ZO NM NM NM NB NB
3 仿真结果及分析
将实际参数代入式(5)中可得移相全桥变换器的控制-输出传递函数为
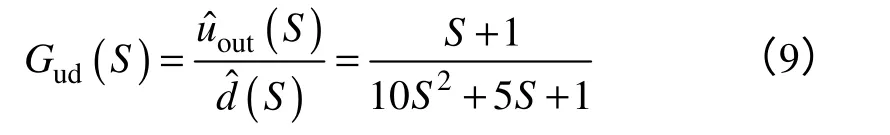
传统PID和自适应模糊PID控制对比的Matlab仿真模型如图5所示。

图5 传统PID 和自适应模糊PID 控制对比仿真图
为了对比稳态特性,Kp、Ki、Kd都分别设为2、0.3、0.05。仿真结果如图6(a)所示。
由图6(a)仿真结果可知,自适应模糊PID控制的响应时间小于传统PID控制,并能够较快达到稳态,且自适应能力较强,具有很好的自适应性和稳态性能。
为了对比动态特性,在第60个采样时刻加入了50的干扰。仿真结果如图6(b)所示。
由图6(b)仿真结果可知,自适应模糊PID控制比传统PID控制能够在同一干扰下,较快回到稳定值,具有较好的动态响应性能。
4 实验结果与分析
根据所述方案,使用TMS320F28033 数字信号处理器控制移相全桥,实现将96V 输入电压升至正负母线360V 的输出电压,满载为2750W,开关频率为60K。图7为移相全桥实验电路板。

图6 传统PID 与自适应模糊PID 控制特性对比

图7 移相全桥实验电路板
通过实验,由示波器测得图8中的各波形。
其中,图8(a)为母线电压波形图,从图中可看出应用该方案的数字控制能较好地使输出电压稳定到参考电压。可得出该控制方法具有较好的稳态特性。
图8(b)到(d)分别为突加轻载,半载和满载时输出电压的变化波形,可以看出应用该方案的数字控制能较好地使输出电压恢复到参考电压。可得出该控制方法具有较好的动态特性。
从图8(b)可知母线电压跌落20V,母线电压调节时间为45.6ms。 从图8(c)可知母线电压跌落32V,母线电压调节时间为31.2ms。
从图8(d)可知母线电压跌落36V,母线电压调节时间为56ms。
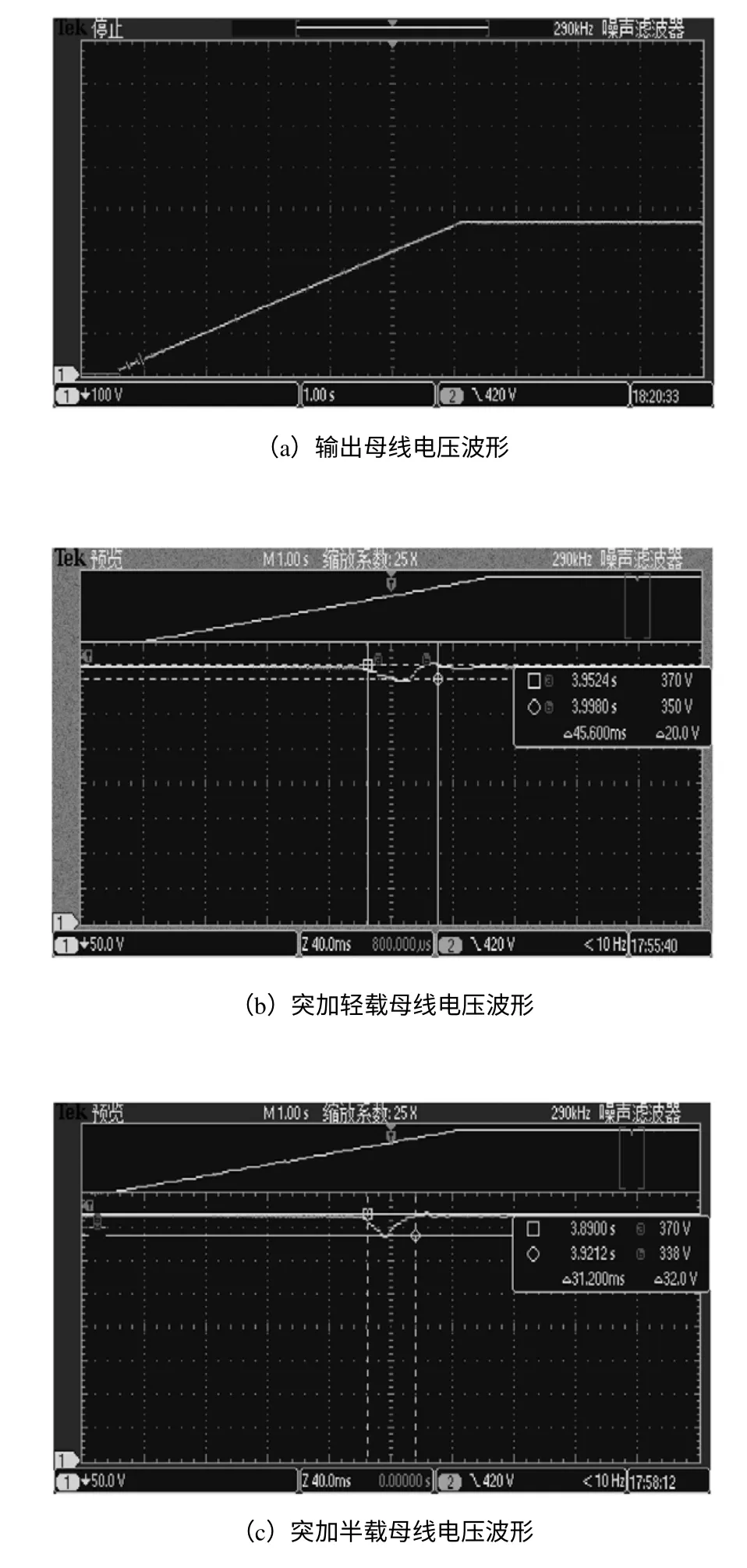
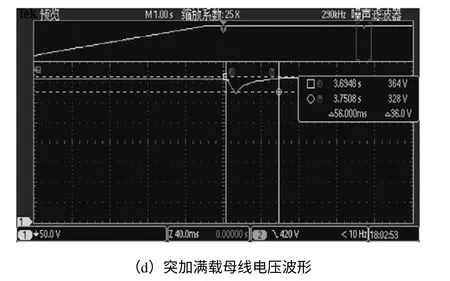
图8 移相全桥实验波形
5 结论
本文在移相全桥先进的动态模型的基础上,推导出新的移相全桥的控制-输出传递函数。在Matlab2012b 的Simulink 仿真环境下,以移相全桥为控制对象,应用fuzzy 模块,分别使用自适应模糊PID 和传统PID 控制方法进行仿真。从仿真结果的稳态特性和动态特性的对比下,我们可知,自适应模糊PID 控制比传统PID 控制具有更好的稳态特性和动态特性。最后并通过实验波形分析,得出自适应模糊PID 控制具有较好的稳态特性和动态特性。
[1] 李琪.PWM 全桥软开关直流变换器的研究[D].杭州:浙江大学,2006.
[2] 洪峰.数字控制移相全桥软开关变换器[D].南京: 南京航空航天大学,2004.
[3] 嵇保健,赵剑锋.DC/DC 变换器数字控制方法研究[J].电力电子技术,2010,44(4): 29-30,76.
[4] 王萍,辛爱芹,邹宇.高性能模糊PID 控制DC/DC变换器[J].电力电子技术,2007,41(8): 102-103.
