基于集对分析的三角模糊数多属性决策方法

胡凌云，袁宏俊，吴庆鹏

(1.安徽财经大学 管理科学与工程学院，安徽 蚌埠233030;2.安徽财经大学 统计与应用数学学院，安徽 蚌埠233030)

多属性决策是对已知方案的评价择优问题进行研究，其理论和方法在实际生活的诸多领域都有广泛应用。三角模糊数多属性决策是其中一类模糊信息的多属性决策问题，很多学者已对其进行深入研究，并取得了丰硕的成果［1］。文献［2］提出基于三角模糊数信息的FCM 聚类算法的迭代方法;文献［3］提出三参数区间数表示灰色模糊数的模糊综合评判方法;文献［4］提出三角模糊数多指标决策问题的理想点法;文献［5］讨论不同距离测度对三角模糊数TOPSIS 决策结果的影响;文献［6］提出一种基于逼近理想解排序(TOPSIS)拓展的决策分析方法。集对分析是研究两个或多个事物同、异、反联系和转化的一种新的不确定系统分析理论［7］，已应用于属性值为区间数的模糊信息的多属性决策问题中;文献［8］针对区间数的多属性决策问题，提出了一种基于集对分析的排序方法;文献［9］依据传统的逼近理想解的排序方法(TOPSIS)基本思路，基于联系数贴近度提出了一种区间数多属性决策新方法;文献［10］将区间数转化为三元联系数，提出了一种解决区间数多属性决策问题的SPA - TOPSIS方法;文献［11］将三角模糊数表示成联系数，提出一种基于联系数的三角模糊数多属性决策评价模型;文献［12］提出基本决策模型的二次联系数概念，利用二次联系数值的变化研究区间数多属性决策。受上述文献的启发，笔者从概率统计的角度提出均值与方差也是三角模糊数特征参数，并注意到三角模糊数的中值相对确定和其他值相对不确定的特点，将三角模糊数的中值直接取作均值，利用均值和方差把属性值和属性权重的三角模糊数转换成集对分析的二元联系数U=a+bi，构建属性值的二元联系数的绝对正理想和绝对负理想，依据传统的逼近理想解的TOPSIS 方法，在联系数距离定义的基础上提出了一种基于集对分析的三角模糊数多属性决策新方法。实证分析表明，所提出的方法步骤简单、可行且结果有效。

1 基本概念

定义1 设R+为正实数集，若=［xL，xM，xN］，其中xL＜xM＜xN∈R+，则称为一个三角模糊数，xL和xN分别为三角模糊数的下确界和上确界，xM为三角模糊数的中值。

由定义1 可知，三角模糊数的中值是确定的，而三角模糊数的其他数值是不确定的，在特定的范围内取值，三角模糊数的表示中蕴含着确定和不确定的信息。

定义2 设R+为正实数集，a，b，c∈R+，i∈［-1，1］，j= -1，则称u=a+bi+cj为同异反三元联系数，简称联系数，a，b，c分别称为联系数的同一度、差异度和对立度。

当c=0 时，称u=a+bi为同异型二元联系数;当a+b+c=1 时，称u=a+bi+cj为归一化同异反三元联系数。

定义3 二元联系数的运算定义。

加法运算：设两个联系数u1=a1+b1i和u2=a2+b2i，则u1和u2的和为：

乘法运算：设两个联系数u1=a1+b1i和u2=a2+b2i，则u1和u2的乘积为：

定义4 若xL＜xM＜xN∈R+，三角模糊数为=［xL，xM，xN］，规定：

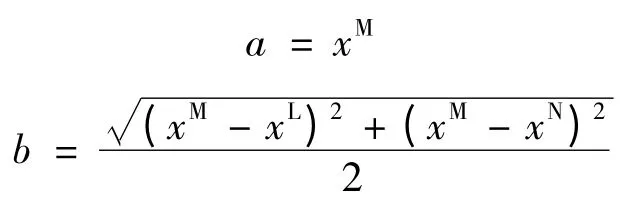
则可将三角模糊数转换成同异型二元联系数，即：

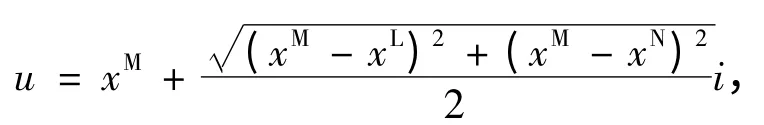
其中i∈［-1，1］。

定义4 给出了一种将三角模糊数转化为二元联系数的方法，三角模糊数的多属性决策问题转化为集对分析的二元联系数多属性决策问题。

定义5 设联系数u1=a1+b1i和u2=a2+b2i，规定u1和u2的联系数距离为：

2 三角模糊数多属性决策问题

在三角模糊数多属性决策问题中，设有m个方案构成方案集：X ={X1，X2，…，Xm}，每个方案各有n个属性值指标，表示第k个方案在第t个属性上的三角模糊数属性值，即］，设第t个属性的权重也可用三角模糊数表示，即1。要求对m个方案作出多属性决策分析，确定这些方案的优劣排序，选出最优方案。

3 三角模糊数多属性决策方法步骤

(2)属性规范化后将三角模糊数转换为同异型二元联系数。根据定义4，将规范化后的各属性值三角模糊数转换为同异型二元联系数：

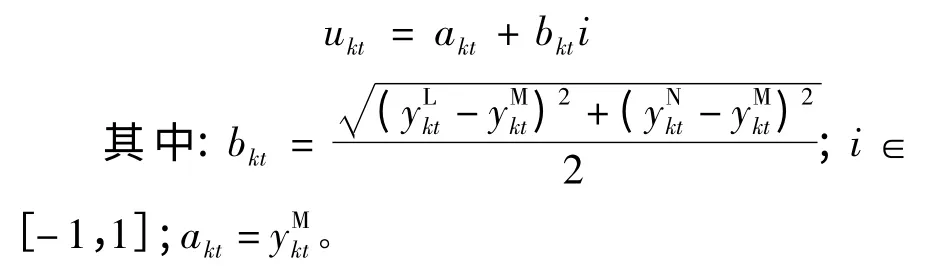
类似地，将各属性权重三角模糊数转换为权重二元联系数：

(3)确定属性值的绝对正理想联系数和绝对负理想联系数。借鉴传统的TOPSIS 排序方法，在属性值二元联系数表示的基础上，构建属性值的绝对正理想联系数：

(4)计算各方案属性联系数与绝对正理想联系数和绝对负理想联系数的距离。由定义3 分别将权重联系数与各类联系数作乘积运算，算得属性值加权联系数、绝对正理想加权联系数和绝对负理想加权联系数。按照定义5 构造属性加权联系数与绝对正(负)理想加权联系数的距离和，对其按属性进行累加算得各方案与绝对正理想的联系数距离各方案与绝对负理想的联系数距离

(5)计算相对联系数距离：

(6)优劣排序和择优。根据步骤(5)中计算出的相对联系数距离Dk的大小对各方案进行优劣排序和择优，Dk值越大方案越好，Dk中最大值对应的方案就是最佳方案。

4 实例分析

为了说明基于集对分析的三角模糊数多属性决策方法的有效性和可行性，采用文献［3］中的实例：影响舰载机机型的性能参数有最大航速V1、越海自由航程V2、最大净载荷V3、购置费V4、可靠性V5和机动灵活性V6等方面，现有4 种机型X1，X2，X3，X4可供选择，各机型性能参数的属性值和属性权重均用三角模糊数表示，经过规范化处理后，给出的数据均是越大越好的效益型数据，具体数据如表1 所示，试确定最佳舰载机机型和优劣排序。

表1 舰载机机型的性能参数属性值和属性权重(已进行规范化处理)

按照步骤(2)，将表1 中三角模糊数转换为同异型二元联系数，具体数据如表2 所示。

根据步骤(3)，由表2 中各舰载机属性值数据的同异型二元联系数可以确定绝对正理想联系数和绝对负理想联系数，具体如下：

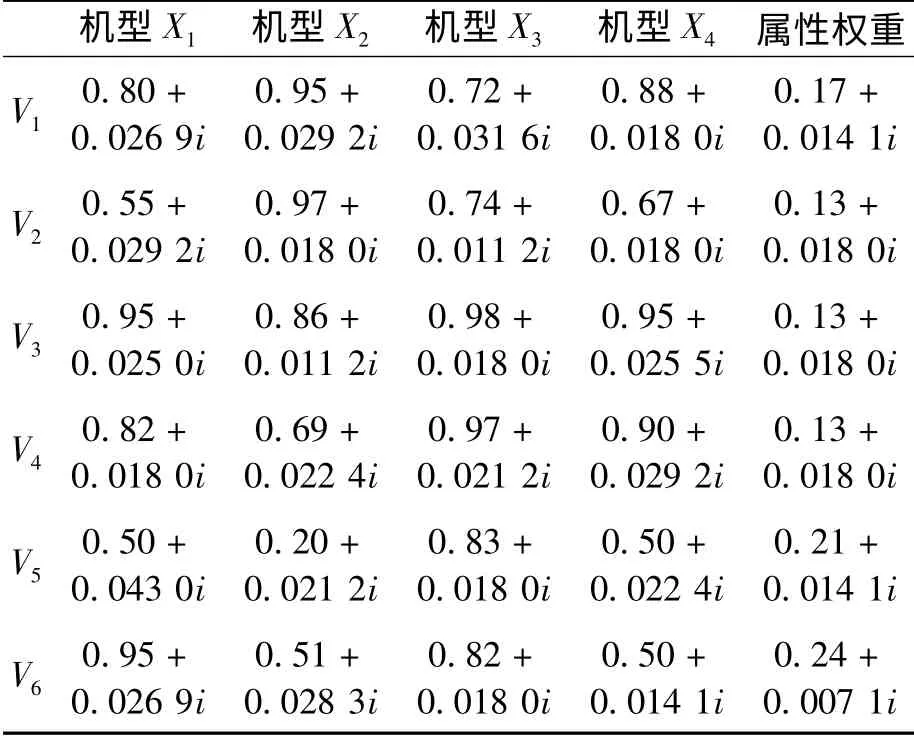
表2 舰载机机型数据的同异型二元联系数

再根据步骤(4)，计算出各舰载机机型的属性值加权联系数与绝对正理想和绝对负理想加权联系数的距离，具体数据如表3 和表4 所示。

表3 属性值加权联系数与绝对正理想加权联系数的距离

表4 属性值加权联系数与绝对负理想加权联系数的距离

由表3 和表4 的数据计算出各舰载机机型的相对联系数距离分别为：

因此这4 种舰载机机型的优劣排序是：X3≻X1≻X4≻X2，第3 种舰载机机型最优，结果与文献［3］的结论一致。

5 结论

三角模糊数的多属性决策是一类模糊信息的多属性决策问题，但由于三角模糊数中蕴含着确定和不确定的信息，借助于集对分析中联系数的处理方法，将三角模糊数的数据处理问题转换为同异型二元联系数的数据处理问题，在属性值二元联系数的表示基础上，构建属性值的绝对正理想联系数和绝对负理想联系数，依据传统的逼近理想解的TOPSIS 方法，以相对联系数距离的大小来对评价方案进行优劣排序，提出了一种集对分析的三角模糊数的多属性决策新方法，实例分析验证了所提出方法是合理且有效的。

［1］徐泽水.不确定多属性决策方法及应用［M］.北京：清华大学出版社，2004：54 -87.

［2］樊治平，于春海，尤天慧.一种基于三角模糊数多指标信息的FCM 聚类算法［J］. 控制与决策，2004(12)：1407 -1411.

［3］卜广志，张宇文.基于三参数区间数的灰色模糊综合评判［J］.系统工程与电子技术，2001(9)：43-45.

［4］许叶军，达庆利.基于理想点的三角模糊数多指标决策法［J］.系统工程与电子技术，2007(9)：1469-1471.

［5］和媛媛，周德群，巩在武.三角模糊数TOPSIS 决策方法及其实验分析［J］.系统工程，2010(11)：95-103.

［6］张市芳.动态区间三角模糊多属性决策的TOPSIS 扩展方法［J］.数学的实践与认识，2013(18)：183-188.

［7］赵克勤.集对分析及其初步应用［M］.杭州：浙江科技出版社，2000：34 -154.

［8］叶跃祥，糜仲春，王宏宇，等.一种基于集对分析的区间数多属性决策方法［J］.系统工程与电子技术，2006(9)：1344 -1347.

［9］汪新凡，杨小娟.基于联系数贴近度的区间数多属性决策方法［J］.数学的实践与认识，2008(3)：16-22.

［10］汪新凡.区间数多属性决策的SPA-TOPSIS 方法［J］.湖南工业大学学报：自然科学版，2008(1)：61-64.

［11］刘秀梅，赵克勤，王传斌.基于联系数的三角模糊数多属性决策新模型［J］.系统工程与电子技术，2009(10)：2399 -2403.

［12］刘秀梅，赵克勤.基于二次联系数的区间数多属性决策方法及应用［J］. 模糊系统与数学，2011(5)：115 -121.