基于低频子带列均衡的图像稀疏表示改进算法
2015-05-27杨媛媛
杨媛媛,谢 涛,陈 伟
(1.武汉理工大学 信息工程学院,湖北 武汉430070;2.南京信息工程大学 海洋科学学院,江苏 南京210044)
随着多媒体技术及通信技术的迅猛发展,大量图像数据需要传输和处理。传统压缩都是基于奈奎斯特准则对图像进行采样的,因此受到了信号带宽的限制。
2006 年,由美国科学院院士DONOHO 等提出的压缩感知(compressed sensing,CS)理论[1-2]为数据压缩开辟了新的道路,近几年CS 也越来越多地用于图像压缩研究。在图像压缩感知中常用小波变换做稀疏表示,但由于其子带分布特性,其稀疏度在列间分布不均匀,致使测量矩阵尺寸、压缩比和恢复时间都受到制约。笔者对压缩感知中基于小波变换的图像信号稀疏表示方法进行了改进,提出了基于低频子带列均衡的图像稀疏表示算法,并进行了实验仿真。
1 理论基础
压缩感知技术对信号的测量是在信号进行稀疏表示后进行的,如图1 所示,因此可以远低于奈奎斯特准则的理论采样率来进行采样。压缩感知理论最大的贡献在于,将数据的采集和压缩过程合二为一,避免了传统理论下采集大量数据,在压缩过程中又丢弃大量冗余数据所造成的资源浪费,大大减少了信号采集、压缩、存储和处理的时间和复杂度。
很多时候,待处理数据本身并不是稀疏的,因此需要对其进行稀疏表示。假设一维信号x∈RN×1,可将其用一组稀疏基Ψ={Ψ1,Ψ2,…,ΨN}进行表示,其表示形式为:


图1 压缩感知理论下信号处理流程
式中,αi为向量x在由Ψ 所表示的稀疏域上的投影稀疏,是N×1 的向量。若α 的取值中,非零值有k个,或者较大系数值有k个,则称α 为k稀疏的。常用的稀疏基有小波基、DCT 基、Gabor基和冗余字典等。在测量时,用向量积对信号x进行M次测量。为保证精确重构,M取值应大于k而小于N。测量过程如下:式中,θ 为M×N矩阵,所得测量值y为1 ×M向量。

测量矩阵若满足约束等距性准则(restricted isometry property,RIP)或测量矩阵和稀疏矩阵不相关,则可通过L1优化问题求解:

目前典型恢复算法为匹配追踪算法(matching pursuit,MP)[3],正交匹配追踪算法(orthogonal matching pursuit,OMP)[4],正则正交匹配追踪算法(regularized orthogonal matching pursuit,ROMP)[5]和压缩采样匹配追踪算法(compressive sampling matching pursuit,CoSaMP)[6]等。
2 基于小波变换的图像压缩感知
一直以来在图像压缩领域中,各标准多采用离散余弦变换(discrete cosine transform,DCT)。其主要问题在于必须对图像进行分块处理,这会引起“方块效应”[7]。近10 年来,小波变换作为一种新兴的变换技术得到了迅速发展,在图像压缩领域,离散小波变换(discrete wavelet transform,DWT)已成为主流变换方法之一。
DWT 对图像进行处理,实际是对图像在小波域进行分解。首先构造尺度函数和小波函数,它们分别具有低通和高通滤波作用,由其组成的正交镜像滤波器可将图像分解为高频子带和低频子带。早期DWT 变换只局限在一层,即先在水平方向进行低通滤波,再在垂直方向进行高通滤波,然后按滤波结果将信号元素重新排列,图2 所示为一层小波变换后的子带分布情况。

图2 一层小波分解子带分布图
其中,LL 子带包含更多图像中的低频信号,HL 子带包含更多垂直方向的高频信息,LH 子带包含更多水平方向的高频信息,HH 包含更多对角线方向的高频信息。基于小波变换的图像压缩感知原理框图如图3 所示。

图3 基于小波变换的图像压缩感知原理框图
首先采用DWT 对图像进行小波分解,然后将其分解系数进行CS 压缩,解压部分用重构算法恢复出小波域系数后,再进行小波合成,即可恢复出原图像。
如果对一层小波分解后的系数进行CS 压缩,几乎恢复不出原图像,这是因为将LL 子带系数一起压缩,破坏了LL 系数的相关性。因此有学者提出只对LH、HL 和HH 子带进行CS 压缩,LL 则用原数据进行传输的方法[8-9]。但该方法对数据的压缩比不高。
考虑到LL 部分仍存在稀疏性,可将LL 部分进一步做小波分解。图4 所示为四层小波分解子带分布图,进一步将低频信号往左上角搬移,保证LL 子带系数尽可能不稀疏,并且经过四层小波分解后,LL 子带系数间的相关性变弱,因此可对所有子带系数统一进行CS 压缩,重构后仍能得到理想效果。

图4 四层小波分解子带分布图
3 基于小波域低频均衡稀疏表示的图像压缩感知
通过压缩感知,可以从M个测量值中还原出原始数据的N个值(M<N),这种压缩的前提条件是这N个值本身是可压缩的,或者说是稀疏的。假设x的稀疏度为k,为了恢复出这k个数据,M的值应该大于k,且如果k增大,M值也必须增大,k减小,M值也相应减小。以四层小波变换为例,在极限情况下,假设所有非零系数都集中在LL4,则其所在的前N/24列的稀疏度为N/24,后N-N/24列的稀疏度为0。则M应大于N/24,压缩比小于24:1。M值对应的是测量矩阵的行数,故测量矩阵应有N/24行。但实际上后N-N/24列稀疏度很低,不需要这么多行的测量矩阵对其进行测量,因此限制了压缩比的提升。并且在重构数据时,以OMP 算法为例,它是对测量后得到的矩阵进行逐列恢复,由于前几列k值较大,所需迭代次数较多,每次迭代,选择的原子就多一列,矩阵变大。即在恢复前几列时矩阵就已经很大了,而每次迭代都要进行矩阵的最小二乘法运算,这样即使后面列的k很小,所需迭代次数很少,但矩阵已经很大了,因此总体运算量很大。
笔者提出一种改进算法,对低频子带进行列均衡,将LL4 中的大值系数均分到每一列的顶端,而各层HL 和HH 子带保持不变。由于经过四层小波分解后,降低了低频子带系数间的相关性,因此在将该部分系数均分到每一列后,再对全部小波系数进行压缩感知,也可获得较高的压缩比和较好的重构质量。由于优化后降低了前面LL4 子块对应列的稀疏度,因此在测量时,可以将测量矩阵的M值设置得更小,以获取更高的压缩比,在同等压缩比的基础上,获得更高的图像质量。由于OMP 恢复算法是逐列重构数据,故可减少LL4 子块对应列重构时的迭代次数,减小恢复这些列所产生的恢复矩阵的大小,抑制计算量的激增,减少运算时间。
假设待处理图像为N×N大小,则经过四层小波分解后,LL4子带大小为假设LL4子带是完全不稀疏的,将其均分到每一列,则在这种理想情况下每一列的稀疏度都变为:

在非理想情况下,LL4 子带也有一定稀疏性,但相对于各层LH 子带来说,其稀疏度明显要高出很多。通过优化,同样可使LL4 对应列的稀疏度变低,其具体均衡方法如图5 所示,其中阴影部分表示大值系数。
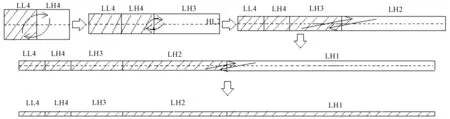
图5 四层小波变换低频子带列均衡原理图
具体操作步骤如下:
(1)将LL4 的低频分量进行上下分块,将其下半部分数据与LH4 的上半部分数据对调,形成新的低频子带,大小为
(2)将步骤(1)得到的低频子带再进行上下分块,将其下半部分数据与LH3 的上半部分数据对调,形成新的低频子带,大小为
(3)将步骤(2)得到的低频子带再进行上下分块,将其下半部分数据与LH2 的上半部分数据对调,形成新的低频子带,大小为
(4)将步骤(3)得到的低频子带再进行上下分块,将其下半部分数据与LH1 的上半部分数据对调,形成新的低频子带,大小为即均匀分布到每一列。
上述方法既实现了低频子带列均衡,也方便了之后对全部小波系数进行CS 压缩和OMP 重构。重构后的数据按照之前的均衡步骤进行反变换,再进行小波合成,即可还原出原始图像。将该方法用于图像压缩感知时的具体流程如图6 所示。

图6 基于低频子带列均衡的图像压缩感知原理框图
通过优化,在设计测量矩阵时即可将M取更小的值且获得更大的压缩比。在同样的压缩比下,由于M远大于每列的k值,因此可获得更好的恢复效果。由于每列的k值很平均且很小,在恢复算法中,前几列的迭代次数较少,矩阵扩大的速度较低,因此整体运算量会显著下降。
4 仿真结果
4.1 峰值信噪比对比
采用256 ×256 大小的Lena 图像作为原始图像,对图像进行四层小波变换,测量矩阵采用高斯随机矩阵,用OMP 算法进行图像重构,对传统四层小波变换图像压缩感知和小波域低频均衡图像压缩感知进行了仿真和结果对比。
分别取M值为32、64、96、128 和164,比较两种算法的峰值信噪比(peak signal to noise ratio,PSNR),结果如表1 所示。
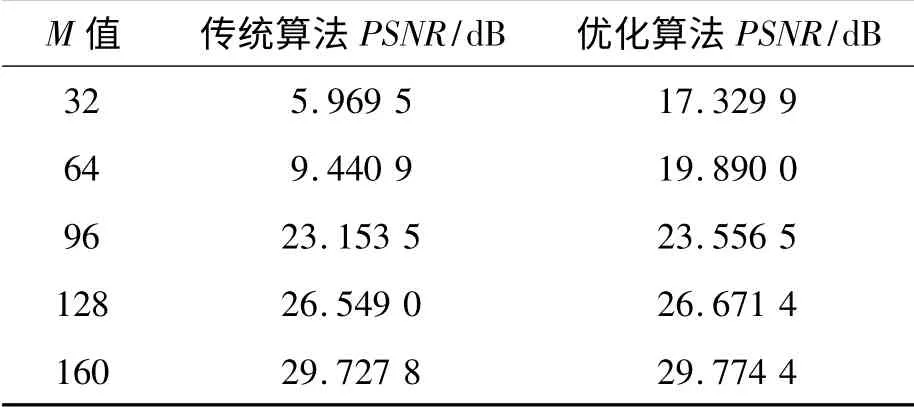
表1 传统算法与优化算法PSNR 对比
由仿真数据可知,优化算法明显比传统算法的PSNR要高,特别是在采样率较低的情况下,传统算法性能会出现严重恶化,而优化算法在这种情况下可大幅提高PSNR,这与之前理论分析是相符的。
4.2 重构时间对比
分别取M值为32、64、96、128 和164,比较两种算法的重构时间,其结果如图7 所示。

图7 两种算法重构时间对比图
由图7 可见,随着采样率的增大,改进算法的运行速度相比原始算法越来越快。采样率低时,迭代次数很少,区别不大。随着采样率增加,低频均衡效果越来越明显,其前面列向量的恢复所需迭代次数明显少于传统算法,矩阵扩充速度减缓,因此整体运算速度大大加快。
4.3 小波域及空域图像对比
经过四层小波分解,得到小波域图像。其左上角有一亮块,对应LL4 中密集的低频分量。经优化处理后,该部分低频分量在列方向上的分布趋于均匀,在小波域图像中表现为亮块消失,分散于各列顶端。
对比M=64 时两种算法所得空域图像,如图8 所示。此时压缩比已经达到了4:1,图8(b)经过优化算法可以恢复出大致图像,而图8(a)采用传统算法,几乎不能恢复。这说明在处理大幅图像信息时,可采用该算法,以较高的采样率获得较好的恢复效果。
5 结论
笔者介绍了压缩感知和稀疏表示的基本理论,对于现有的小波域图像稀疏表示及其在压缩感知中的应用和存在问题进行了分析。根据小波分解系数的分布特点,提出了小波域低频均衡的图像稀疏表示改进算法,通过将低频子带均分到每一列,降低前面列的稀疏度。将其应用于压缩感知,则可减小测量矩阵大小,提高压缩比,降低恢复时间,或在同样的压缩比下提高图像恢复质量。在不同压缩比下对传统算法和优化算法进行了仿真对比,结果显示该算法与传统基于小波变换的压缩感知算法相比,在恢复效果和节省运算时间上均有一定程度的改善。

图8 M=64 时恢复空域图像对比
[1]DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2]CANDES E. Compressive sampling[C]∥Proceedings of the International Congress of Mathematicians. Madrid:[s.n.],2006:1433 -1452.
[3]MALLAT S,ZHANG Z. Matching pursuit in a time -frequency dictionary[J]. IEEE Trans Signal Processing,1993,41(12):3397 -3415.
[4]TROPP J,GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit [J].IEEE Trans Inform Theory,2007,53(12):4655-4666.
[5]NEEDELL D,VERSHYNIN R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Found Comput Math,2009,9(3):317-334.
[6]NEEDELL D,TROPP J A. CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2008,26(3):301 -321.
[7]CHEN J L,YANG J. Improved image coding algorithm based on embeded zerotree wavelet[J]. Image and Signal Processing,2009,9(2):1 -4.
[8]张砺佳. 基于小波变换的图像压缩编码研究[D].北京:中国科学院研究生院,2007.
[9]CEN Y G,CHEN X F,CEN L H,et al. Compressed sensing based on the single layer wavelet transform for image processing[J]. Journal on Communications,2010,31(8A):52 -55.
