启用数学软件讲授高职数学的新思路

◆黄毓先 黄艳茹

作者：黄毓先，北京电子科技职业学院副教授，研究方向为数学；黄艳茹，北京电子科技职业学院讲师，研究方向为数学（100029）。

1 引言

通过近些年来的高职数学教学，及对以往学生的了解，北京电子科技职业学院生源层次复杂，分三年制及五年制高职。三年制又分为本地生源和外地生源，两者也存在差异。五年制高职，普遍来讲，文化基础更差。整体而言，高职学生思想较活跃，但上课注意力不集中，自我约束能力差。课堂上，大多数学生对数学学习缺乏信心和兴趣。按照高职院校学生的培养方向与要求，结合学校高职学生的状况与特点和对课堂教学模式的分析与研究，在教学中采用适宜的教学方式，对探求适合职业学院学生的教学之路有着重要意义。

随着高等教育从精英型向大众型转化，传统的数学教学模式及方式已经很难适应当前形势，正面临越来越多的问题和困难。多年来，数学教学内容、方法和手段变化较少，不能体现数学在科技和现实生活中所起的重要作用，学生缺乏运用数学的思想和方法来解决实际问题的能力。

2 数学实验

随着科学技术的发展及为了适应新的形势，数学教学也面临改革，特别是在信息化时代，要求数学教学增强实践性，数学实验就是基于此而产生的。

物理实验和化学实验是知道的，就是利用仪器设备，通过实验来了解物理现象和化学物质等的特性。同样可通过数学实验来了解数学问题的特性并解决对应的数学问题。过去，因为实验设备、条件、手段的问题，难以解决数学的实验问题。随着计算机的发展，软件功能的增强，许多数学问题都可以由计算机来解决，也为教师利用计算机为工具，用数学实验解决数学问题提供了可能。

数学实验软件平台由若干数学软件组成，它提供各种强大的运算、统计、求解、作图等功能。数学软件按用途，一般可分为通用数学软件和专用数学软件两大类。有关数学软件的类型及选用这里不再详述，见相关方面的介绍。

本文的目的在于探讨高职数学课的教学中引入计算机应用，启用Mathematica 软件讲解一元微积分为主线，根据高职学生理论基础差的特点，改变教学模式，通过数学软件的使用，跨过微积分传统教学中的若干环节，使得所要求解的问题变得简单化。因为学生基础差的原因，强调应用为主、逻辑推理为辅的主导思想，某种程度上讲可以达到事半功倍的效果，促进理实一体化教学。

从某种意义上讲，Mathematica 是一个复杂的、功能强大的解决计算问题的工具，主要功能包括是三个方面：符号演算、数值计算和图形。它可以自动地完成许多复杂的计算工作。显然，针对高职数学中的主要内容，尤其是涉及有关微积分方面的知识，通过Mathematica 三大功能，几乎很多问题都能很轻易解决，这是笔者选用它进行课程改革的主要原因。

3 启用数学软件教学模式

本文就一元微积分主要内容引入计算机应用后，探讨两种教学模式的优劣。传统的教学模式是：数学概念的背景→定义→几何意义→推导公式或介绍相关定理→性质→例题→作业等。

笔者的总体思路在于讲解简单的数学概念来源，类似的问题拿来，用数学软件直接解决，省去若干繁琐的中间步骤，得到期望的结果。这和过去秀水街卖衣服的小贩，虽然自身文化水平很低，小学没毕业，有的还没上过学，口算心算很困难，但能用简易计算器不耽误挣钱一个道理。某种意义下，要的是结果，不注重过程，有些情况下，过程其实已经不再重要。

传统的教学模式强调的是中间过程（背景、定义、定理等，注重逻辑推理等），当然对学生的基础要求较高，但不同的教学对象应采用不同的教学思路。今天的学生是不同层次的高职学生，采用的教学模式应该有很强的针对性，尤其是对基础差的高职学生，省去理论上的若干环节，用数学软件直接得到相应的结果，在笔者看来，不失为一种高效的方法。当然，对于基础好的学生，附加上相应的理论升级教学方法。

下面就用数学软件Mathematica 来讲解一元微积分涉及的主要内容。一元微积分涵盖的教学内容包括函数、极限、导数与微分、导数的应用、不定积分、定积分及其应用。在使用Mathematica 软件的环境下，由于篇幅所限，将相对独立的内容（极限、不定积分）及后面章节基础会用到的内容（导数与微分）略去。

总体思路：介绍简单数学概念→数学软件使用→软件求解结果。

图中涉及的Mathematica 操作命令有定义函数、作图、求导数、求解方程、化简、求积分、求面积、有关分析等。实际操作过程中，可根据需要选择相关命令，有些命令顺序相关性不大。格式除本文介绍的以外，详见有关书籍或Mathematica 软件帮助。

案例1：函数及函数作图（见图1）。

案例2：导数的应用（见图2 及图3）。

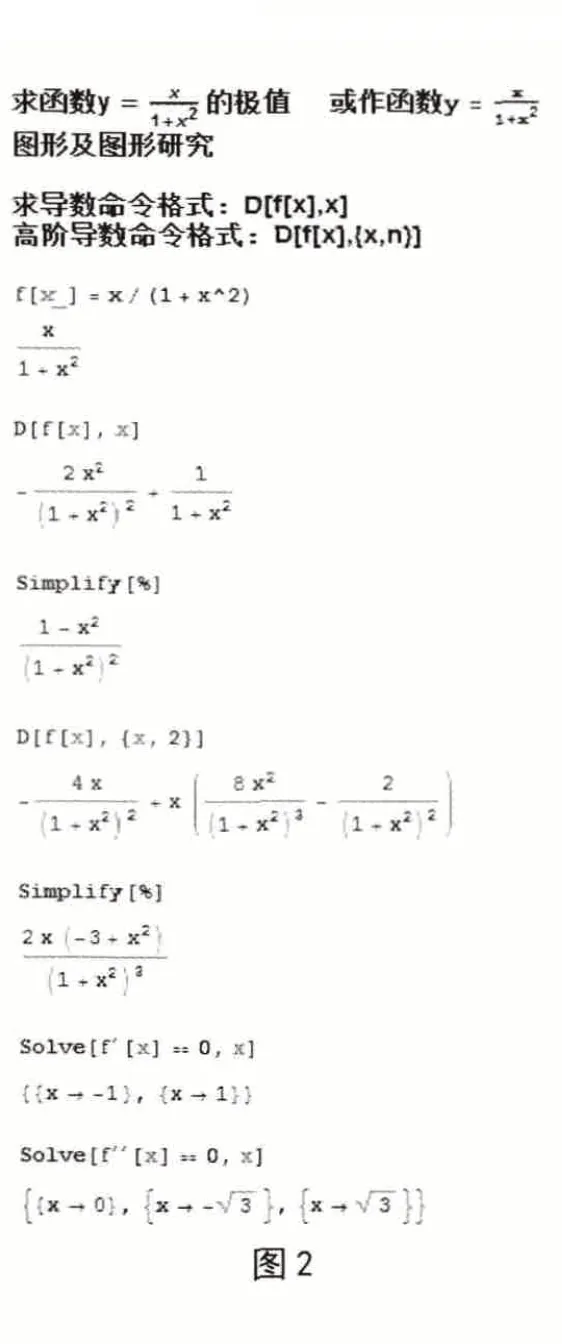
案例3：定积分及定积分应用（见图4）。

以上用Mathematica 的解法描述了一元微积分的主要内容，可从实际案例体会授课方式上带来的变化，再与理论教学对比这些案例。

4 数学理论课与实验课的结合方式

数学实验课主要有三种形式：集中培训、与理论课同步进行（理实一体化）、先培训Mathematica 基础后再与理论课同步进行。

1）集中培训。由于这种形式需要某一集中时间段，不能及时反映数学理论课的教学内容，从而使得教学中常常仅涉及数学软件本身，因而达不到数学实验课所应起到的作用。

2）数学软件与数学理论课同步进行。从理论上讲，可使数学理论学习随时有数学软件的帮助，但软件的操作要占用相当的时间，数学实验课要用机房，上机时间必须固定，硬件环境不够的学校会有些问题。课时安排（1:1）或（1:2），先理论后实验，安排不当有间隔，可能会使得理论课与实验课脱节。

3）软件基础先行。在入学后进行集中培训，讲述基本的软件操作规则，理论课教学中再根据内容随时补充，并伴有机房开放时间内的（学生自己的）随时练习和辅助学习，应该更能发挥数学软件对数学理论课教学的辅助作用。

另外，数学实验课应不排除与专业课结合，形成一种结合专业应用而进行的数学应用课程设计。

5 结论

综上所述，本文以Mathematica 作为软件工具，结合一元微积分的数学内容，用数学软件求解来组织教学内容，省略了传统数学教学理论上难懂的过程，定义、定理、性质等推导过程，直接用数学软件解题，让问题变得简单化，在学生能够体会的计算机环境下，应用软件解决问题。这里推荐采用“案例教学、任务驱动”教学法讲解知识与训练技能，适用于理论、实践一体化教学，以此Mathematica为基础，为将来问题的提出、解决或后面各门课程讲解打下一定的基础。可以预见，通过计算机强大的运算、图形功能和方便的数学软件，使学生可以自由地选择算法和软件，在屏幕上通过数值的、几何的观察、联想、类比，去发现线索，探讨规律，进一步激发学生学好数学的兴趣，为他们的成长打下坚实的基础，为学校的课程改革提供一种可行的模式。

[1]孙平，张忠毅，范广玲.高等数学及其实验[M].哈尔滨:哈尔滨工程大学出版社，2013.

[2]黄毓先.高职数学教学中引入计算机应用方案探析[M].中国教育技术装备，2015(10):133-136.