四维双曲空间中的超曲面

朱 鹏

（江苏理工学院数理学院，江苏 常州 213001）

四维双曲空间中的超曲面

朱 鹏

（江苏理工学院数理学院，江苏 常州 213001）

研究四维双曲空间H4中完备非紧1－极小稳定超曲面的整体性质，得到如下结论：若平均曲率和Gauss－Kronecker曲率满足适当的条件，则双曲空间H4中不存在具有多项式体积增长的完备非紧1－极小稳定超曲面.

多项式体积增长；1－极小稳定超曲面；双曲空间

关于欧氏空间中超曲面整体性质的刻画，已有众多学者给出了研究结果.Cheng等［1］证明了欧氏空间中具有常纯量曲率和非负截面曲率的完备非紧超曲面一定是广义的圆柱面.随后，受Shen等［2］的启发，Alencar等［3］证明了四维欧氏空间中不存在具有非零Gauss－Kronecker曲率和有限全曲率的完备非紧1－极小稳定超曲面.Chern［4］给出了n维欧氏空间中不存在Ricci曲率具有负常数上界的全图，Alencar在文献［3］3302中进一步证明了n维欧氏空间中不存在负纯量曲率的全图.最近，Silva［5］结合Nelli等［6］的技术证明了平均曲率和Gauss－Kronecker曲率在适当的限制下，四维欧氏空间中不存在具有零纯量曲率、多项式体积增长的完备1－极小稳定超曲面.Cavalacante［7］，Zhu［8］等都证明了欧氏空间上有限全曲率的完备超曲面的约化L2上同调空间的维数有限.本文将研究四维双曲空间H4中完备非紧1－极小稳定超曲面的整体性质.

1 预备知识

三维黎曼流形M3具有多项式体积增长，是指存在γ∈（0，3］使得M3中每一点p，都有limr→∞vol（Br（p））／rγ＜＋∞，这里vol（Br（p））是M3中以p为中心，r为半径测地球的体积.设M3是三维完备黎曼流形，映射x：M3→H4是等距浸入，算子A：T p M→T p M为映射x的第二基本形式，其中T p M表示流形M在p点处的切空间.设λ1，λ2，λ3为A的特征值，关于λ1，λ2，λ3的第r个对称函数Sr（r＝1，2，3）定义为

称H r＝Sr／为等距浸入的第r个平均曲率［9］.显然，H1是平均曲率，H3是Gauss－Kronecker曲率，H2与M3的纯量曲率相差常数－1.若H r＋1＝0，则称超曲面M3为r－极小超曲面.

2 主要结果及其证明

研究四维双曲空间H4中完备非紧1－极小稳定超曲面的整体性质，得到如下结果.

定理1 对任意给定的正常数δ1，δ2，双曲空间H4中不存在满足如下条件的完备非紧1－极小稳定超曲面：

i）具有多项式体积增长；

再由P1的正定性，有

结合式（2）（3）（4）和〈P1（X），X〉≤2S1｜X｜2，得不等式

选取φ＝φ3＋2q／2，则有

再结合式（5）和式（6），得

由Young不等式xy≤a－1x a＋b－1yb，其中正实数a，b满足a－1＋b－1＝1，得

其中a为待定的正常数.结合式（7），有

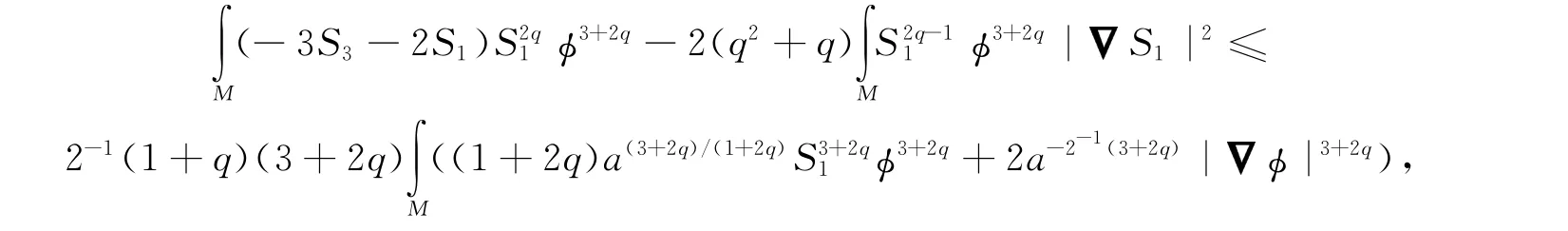
即

其中

注意到（－2H－K）／（H3）≥δ1，｜ （1／H）｜≤δ2，这意味着（－2S1－3S3）／（）≥δ1／9，｜ （1／S1）｜≤δ2／3.于是，

选择充分小的q和a使得T1＞0，并选择仅依赖于到某个固定点p的距离为r的函数

结合式（8），可得

由于M3具有多项式体积增长，令R→＋∞，得证S1为零.这与假设矛盾，证毕.

［1］CHENG Shiuyuen，YAU Shingtung.Hypersurfaces with constant scalar curvature［J］.Math Ann，1977，225：195－204.

［2］SHEN Yibing，ZHU Xiaohua.On stable complete minimal hypersurfaces in Rn＋1［J］.Amer J Math，1998，120（1）：103－116.

［3］ALENCAR H，SANTOS W，ZHOU Detang.Stable hypersurfaces with constant scalar curvature［J］.Proc Amer Math Soc，2010，138（9）：3301－3312.

［4］CHERN Shiingshen.On the curvatures of a piece of hypersurface in Euclidean space［J］.Abh Math Sem Univ Hamburg，1965，29：77－91.

［5］SILVA NETO G.On stable hypersurfaces with vanishing scalar curvature［J］.Math Z，2014，277（1／2）：481－497.

［6］NELLI B，SORET M.Stably embedded minimal hypersurfaces［J］.Math Z，2007，255（3）：493－514.

［7］CAVALCANTE M P，MIRANDOLA H，VITÓRIO F.L2－harmonic 1－forms on submanifolds with finite total curvature［J］.J Geom Anal，2014，24（1）：205－222.

［8］ZHU Peng，GAN Wenzhen，ZHOU Jiuru.On the reducedL2cohomology on complete hypersurfaces in Euclidean spaces［J］.Arch Math（Basel），2015，105（2）：189－200.

［9］ALENCAR H，do CARMO M，ELBERT M F.Stability of hypersurfaces with vanishing r－mean curvatures in Euclidean spaces［J］.J Reine Angew Math，2003，554：201－216.

［10］REILLY R C.Variational properties of functions of the mean curvatures of hypersurfaces in space forms［J］.J Differ Geom，1973，8：465－477.

［11］ALENCAR H，do CARMO M，COLARES A G.Stable hypersurfaces with constant scalar curvature［J］.Math Z，1993，213（1）：117－131.

［12］HOUNIE J，LEITE M L.Two－ended hypersurfaces with zero scalar curvature［J］.Indiana Univ Math J，1999，48（3）：867－882.

Hypersurfaces in a 4－dimensional hyperbolic space

ZHU Peng

（Sch of Math ＆Phys，Jiangsu Univ of Tech，Changzhou 213001，China）

This paper studies the global properties of complete noncompact 1－minimal stable hypersurfaces in a 4－dimensional hyperbolic spaceH4.It is obtained that there is no complete noncompact 1－minimal stable hypersurfaces inH4with polynomial volume growth in case of the restriction of the mean curvature and Gauss－Kronecker curvature.

polynomial volume growth；1－minimal stable hypersurfaces；hyperbolic space

O 186.12

A

1007－824X（2015）04－0044－03

2015－04－13.E－mail：zhupeng＠jsut.edu.cn.

国家自然科学基金资助项目（11471145，11371309）；江苏省“青蓝工程”优秀青年骨干教师培养基金资助项目（苏教［2014］23号）.

朱鹏.四维双曲空间中的超曲面 ［J］.扬州大学学报（自然科学版），2015，18（4）：44－46.

（责任编辑 青 禾）