以研立学 因学而教

周艳

[摘 要]“梯形的面积计算”是在学生已经熟练掌握了长方形、正方形，尤其是平行四边形和三角形的面积计算和梯形的认识的基础上学习的数学问题。特级教师周卫东教学此内容时，没有沿袭以往的教学思路，亦步亦趋地让学生从“0”开始进行学习，而是立足于学生已有的数学知识和经验，以研立学，因学而教，通过引导点拨让学生经历了自主研究与发现，最终获得提升的学习过程，让学生在再创造中自我建构新知、解决问题。

[关键词]自我建构 数学思考 数学思想 数学活动经验

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）14-017

【片断一】各小组交流如何计算梯形面积后汇报。

生1：我是这样想的，两个完全一样的三角形可以拼成一个平行四边形，那么两个完全一样的梯形也可以拼成一个平行四边形，拼成的平行四边形的底等于梯形的上底加下底，平行四边形的高就是梯形的高，而梯形的面积就这个平行四边形的一半，所以梯形的面积=（上底+下底）×高÷2。（方法1）

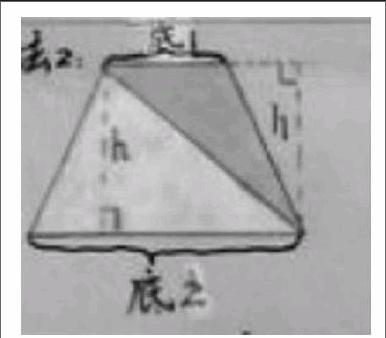
生2：我有不同的方法。把梯形分成两个三角形，因为三角形的面积我们是会算的，梯形的面积=三角形1的面积+三角形2的面积，三角形1的面积就是（底1×高÷2），三角形2的面积就是（底2×高÷2），如图1，底1就是梯形的上底，底2就是梯形的下底，梯形的高也就是三角形的高，所以梯形的面积就是“（梯形上底+梯形下底）×高÷2”。（方法2）

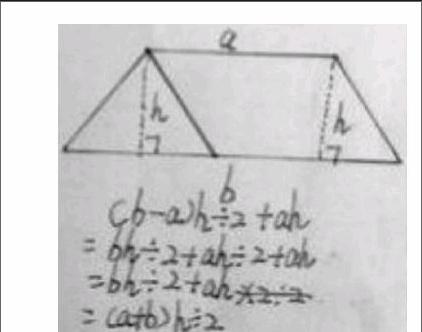
生3：还可以把梯形分成平行四边形和三角形。平行四边形的面积是底×高，三角形面积是底×高÷2，平行四边形的底是梯形上底，三角形的底是（梯形下底-梯形上底）。那么平行四边形的面积就是“梯形上底×高”，三角形面积是“（梯形下底-梯形上底）×高÷2”，把两部分合起来就是“梯形上底×高+（梯形下底-梯形上底）×高÷2”，把这个算式整理一下就是“梯形下底×高÷2+梯形上底×高÷2”，也就是“（梯形上底+梯形下底）×高÷2”。（方法3）

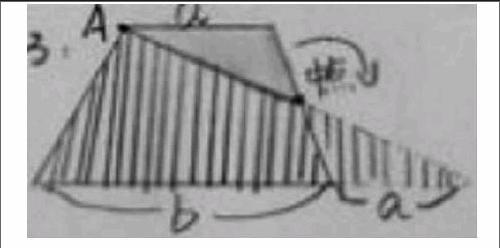
生4：我还有不同的方法。在梯形的腰上找到中点，连接A点和中点，将这个三角形旋转，得到一个新的三角形，新三角形的面积和原来梯形面积相同，新三角形的面积是（底×高÷2），新三角形的底就是（梯形上底+梯形下底），所以梯形的面积就是（梯形上底+梯形下底）×高÷2。（方法4）

生5：我和生4的方法有一点类似，把梯形沿着腰的中点分割开，然后补成一个平行四边形。这个拼成的平行四边形的面积和原来梯形的面积是一样的，平行四边形的底就是梯形的上底加下底的和，平行四边形的高是梯形的高的一半，平行四边形的面积是（梯形上底+梯形下底）×（高÷2），所以梯形的面积也就是（梯形上底+梯形下底）×高÷2。（方法5）

生6：我想问为什么从中点切开，补成的这个图形就是一个平行四边形呢？

生7：我可以用一个梯形剪一下。（操作演示了从梯形中位线剪开拼成平行四边形的过程）

师：生6的问题提得很好，说明他很善于思考，不过生7也很爱懂脑筋，能想到用一个梯形进行简拼。生5的推理方法是正确的，但是以我们目前学习的方法还不能严格地证明这种推导方法，有兴趣的同学课后可以再学习。

师：在这里，老师还有一个问题，在这些方法中都要除以2，为什么梯形的面积计算要除以2呢？

生8：因为用两个完全一样的梯形可以拼成平行四边形。我们先算了平行四边形的面积，因为平行四边形是由两个完全相同的梯形拼起来的，所以算梯形的面积当然要用平行四边形的面积除以2了。

……

《礼记·学记》中记载：“独学而无友，则孤陋而寡闻。”学习需要有独立思考的过程，但更需要有合作交流的成分，课堂展示交流充分将学生的学习收获分享于众，展示交流为他们个性化的思考提供了巨大的空间，从而使学生获得一种莫大的成就感。首先让学生充分运用割补、平移和旋转等策略，通过迁移转化，沟通了平面图形之间的内在联系，得出公式推导的多种方法，落脚点都是梯形的面积计算公式，最后，再将梯形面积计算公式中“除以2”的难点留给学生去解释。整个教学过程中教师退居讲台之后，只在学生有疑难处适时出手，强调了重点，突破难点，真正落实了教学目标。

【片断二】师：刚才同学们想出了不同的方法推导出了梯形的面积计算公式，非常了不起，反观这几种方法，你能找一找这些方法之间的相同和不同吗？

生1：这些方法都是将梯形转化成我们已经学过的图形来计算面积，然后推导出梯形面积计算的方法的。

生2：方法2和方法4是把梯形转化成三角形来算的。

生3：方法1和方法5是把梯形转化成平行四边形来算的。

师：在转化时用的方法上有什么类似的地方吗？

生4：方法2、方法3是把梯形分割成我们学过的图形来算的。

师：这两种方法用到了分割的策略。（板书“分割”）

生5：方法4、方法5是把梯形剪开，然后再拼成新的图形来算的。

师：这两种方法用到了剪拼的策略。（板书“剪拼”）

师：这些方法都是将梯形转化成我们学过的图形进行计算的。

……

对于梯形面积计算公式的推导，多样的方法并非教学目的，而是通过多种方法的展示，让学生之间可以相互学习、相互启发、开拓思路、启迪智慧。教师在尊重学生主体地位的同时，还应该时刻记住自己的主导身份，适时点拨，揭示知识的数学实质及体现的数学思想，帮助学生理清相关知识之间的联系与区别。在这里，学生面对多种推导方法，到底要从这些方法中学到什么？这是我们教师需要心中有数的，因为具体的知识应用是十分有限的，解决问题的方法与策略才是更高层次的学习内容，是我们所追求的教学目标。在面积推导中蕴含了丰富的转化策略，和将未知转化成已知的数学思想，教师通过适当的提问，引导学生再次反观众多方法，异中求同，提炼了“剪拼、分割”的转化策略，使学生深刻体会到转化的数学思想，为后续的相关学习积累了有效的数学活动经验。

【片断三】学生在明确了梯形的面积计算公式后，已经会运用梯形的面积计算公式进行简单计算。周老师没有就此打住，而是出示了一道变式题，将学生的思维引向深处。

生：46-20=26（米），26×20÷2=260（平方米）。

师：这里没有给出梯形的上底和下底，你是怎么求的？

生：我们求梯形的面积时要知道上底和下底是为了知道上底和下底的和，在这里求出“46-20”就可以知道上底和下底的和了，所以就可以求梯形的面积了。

师：做了这道题，你有什么想法？

生：不要生搬硬套梯形的面积公式，有时候不知道上底和下底分别是多少也没关系，关键是要知道梯形上底和下底的和。

……

学习是一种积累的过程，它不在于解决问题的某种小技巧，而是一种面对新问题勇于尝试与探究的精神与勇气，最重要的思想是让大多数人能够以他们可以接受的方式主动学习，让所有人能从学习中获得自信，和一份积极向上的精神状态。学习“梯形面积的计算”这一内容，直接套用梯形的面积公式进行计算，大部分学生都可以很熟练，然而，这样的基础练习容易让学生产生思维定式，影响对梯形面积计算的灵活应用，而这道练习题的呈现，打破了学生原先的思考套路，让他们在练习中自己发现计算梯形面积时并不是一定要知道梯形的上底和下底分别是多少，关键是要知道上底加下底的和，从而领会梯形面积计算的核心要义，真正实现了“让人人都获得良好的数学教育，不同的人在数学上得到不同的发展”课程目标要求。

（责编 金 铃）