注重数学推理发展数学思维
2015-05-25胡安弟
胡安弟
推理是科学发现的一把金钥匙,也是数学思维的重要方式之一。在小学数学教学中,教师要发展学生的思考能力,提升学生的数学思维,就要培养他们的推理能力,帮助其养成言必有据、条分缕析的思维习惯,积累思维经验,形成良好的问题解决能力。那么,在教学实践中如何培养小学生的数学推理能力呢?笔者现根据自己的教学经验,谈谈认识。
一、猜想打开推理的大门
猜想是一种数学想象,这种想象并不符合逻辑,是凭借经验和直觉推断出来的一种伪结论,需要进一步验证和探究。客观上,数学猜想能够为数学发现提供机会,同时也能够给问题的解决创造条件。在小学数学教学中,因小学生好奇心强、想象力丰富,教师要积极创设有效的问题情境,通过认知冲突的制造,引发学生的猜想,带领学生推开数学推理的大门。
如在教学“圆的周长”时,创设了这样的情境:两只蚂蚁保持相同速度,从a点开始绕着正方形和圆周爬,哪只蚂蚁最先回到起点?要解决这个问题,需要学生从圆与正方形的关系上来思考。也就是说,圆的周长跟什么有关,正方形的周长跟什么有关,这是问题的关键。基于此,教师让学生提出自己的猜想,有的学生认为圆的周长是直径的2倍多,也有学生猜想圆的周长超过了直径的4倍之多,还有学生认为不可能超出4倍。
在圆的学习中,周长与直径的倍数关系是重点也是难点,通过猜想引导学生合情推理,从而确定圆的周长与直径倍数关系的范围,这就为下一步深入探究提供了思路。
学起于思,思源于疑。小学生根据自己的猜想不断调整,使思维始终处于一种积极主动、活跃的状态,不但在疑问中主动探究,而且在解答疑问中习得方法,领悟新知,初步建立起抽象思维和空间观念。由此可见,从数学想象展开有依据的数学猜想,是带领学生进行数学推理的第一步。
二、操作积累推理的经验
小学生主要以感性思维为主,抽象思维较为薄弱。教学中加强实践操作,能够丰富数学表象,积累学生的数学经验,对数学推理提供重要的感性积累。
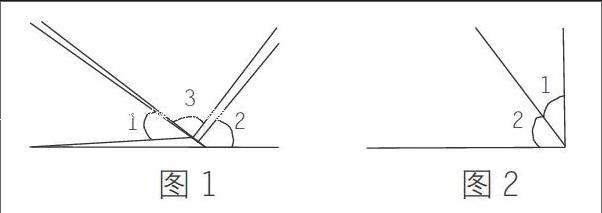
如在教学“三角形内角和”这一内容时,为了让学生对“三角形的内角和是180度”这个结论的推理有清晰的认知,特地带领学生展开操作实践。先从特殊的直角三角形入手,采取量一量、算一算、拼一拼的办法,让学生经历整个过程。有的学生将三个角拼成了一个平角(如图1),有的学生将两个锐角叠加在一个直角上(如图2)。学生一边操作,一边对三角形的内角和有了直观的认知。这时,又出了一道综合性问题:如果∠1+∠2=∠3,那么这个三角形一定会是直角三角形吗?学生因为已经有了之前的操作和实践,再根据三角形内角和180度的推理经验,能够很自信地进行判断,并说明其中的理由。
从以上教学过程可以看到,教师先让学生动手实践,根据操作实践形成感性认识,积累感性经验,然后对事物进行判断推理,就能够使学生的感性经验上升为理性认知,促进学生推理能力由最初的直观性向抽象性发展,由此使思维能力也由感性发展为抽象的理性。
三、演绎形成推理的逻辑
数学思维的最终体现是要落实在对逻辑推理的有效演绎上。教学中,学生之间的能力往往会有差异。这就需要教师实例指导,一边带领学生进行推理演绎,一边教给学生推理的规范,在步步追问中使学生能够有条理地表达,并养成推理使之符合有序、有据的逻辑性品质。
如在教学“周长”这一内容时,设置了这样一道习题:在周长为6厘米的长方形中,如果在中间加一条线段,长方形的周长是多少厘米?面对这个问题,学生的解决办法出现了两种分歧:一种认为周长应该是7厘米,还有一种认为周长应该是6厘米。
到底哪一种才是正确的呢?此时,教师并不评判,而是以此为契机,让学生展开推理,弄清楚几个问题:首先,要弄清楚什么是周长,在这个封闭的长方形图形里,周长就是指封闭一周的长度;紧接着需要学生弄清楚,从A点出发沿着长方形的四条边转一周,是否还要回到A点,答案是肯定的。那也就是说,这一周还是围绕着长方形转了一圈。根据以上推理,学生很快就有了清晰的思路,并且通过推理得到最终的结论:这个长方形的周长还是6厘米。
在以上教学环节的引导中,学生从已知条件出发对周长的概念进行了复习巩固,然后分析了从A点出发这个条件需要解决的问题,这样一步步深入探究,使数学逻辑缜密细致,不仅能够提高他们语言表达的条理性,也提高了学生演绎推理的能力。
总之,数学推理是数学逻辑思维的一种形式,也是重要的数学思想方法。小学数学离不开推理,通过已有旧知进行演绎推理,从而引出新知,探究新知。因而,在小学数学教学中,教师不能忽略推理能力的培养,而是要创设认知环境,给学生提供系统化的推理范本,展开推理练习,以此才能有效提升学生的数学推理能力,发展数学思维。
