计及磁场耦合特性的无轴承开关磁阻电机的电磁设计

刘泽远，杨 艳

(南京邮电大学自动化学院，江苏南京210023)

计及磁场耦合特性的无轴承开关磁阻电机的电磁设计

刘泽远，杨 艳

(南京邮电大学自动化学院，江苏南京210023)

结合无轴承开关磁阻电机(BSRM)数学模型的推导及其运行特点，提出了12/8极BSRM可计及转矩绕组和悬浮绕组磁耦合特性的主体尺寸计算公式。考虑到BSRM的悬浮力随位置角和电流的变化规律，利用平均悬浮力设计BSRM的最大径向负载要求。基于BSRM的最恶劣工作状况，提出了基于绕组峰值电流计算绕组匝数的方法。最后，分析了BSRM定、转子极弧选取的原则，并设计了一台实验样机。

无轴承开关磁阻电机;电机设计;转矩;悬浮力

1 引言

无轴承开关磁阻电机(BSRM)不仅具有磁悬浮电机无摩擦、无接触、无润滑和长寿命等一系列优良特点，还兼有开关磁阻电机(SRM)的结构简单、控制灵活、容错能力强和高速适应性强等优点［1，2］。因此，BSRM在航空高速、超高速起动发电机领域有独特优势。

目前，关于BSRM的研究主要集中在其控制策略［3-5］、数学模型［6，7］及功率变换器［8，9］等方面，少有涉及其本体设计的研究［10，11］。

就结构而言，BSRM仅在定子上比SRM多了一套悬浮绕组，两者的设计方法既有相同点，又有不同之处。相同点为两者均为双凸极结构，BSRM的基本尺寸可参考SRM的设计方法，如电机极高、轭厚等尺寸的计算。不同之处在于BSRM的控制策略和数学模型均比SRM复杂得多，还多了一个悬浮力指标，这对其本体设计提出了新要求;而且转矩绕组和悬浮绕组间的强磁耦合特性，也增加了其本体设计的难度。

为此，本文将结合12/8极BSRM的运行特点，研究其电磁设计方法;涉及到了其主体尺寸计算公式，径向悬浮力设计，绕组参数的计算及定、转子极弧的选取等。

2 本体尺寸计算

BSRM每个定子上均绕有转矩绕组和悬浮绕组(如图1所示)，二者对转矩和悬浮力均有贡献，且两类绕组间还存在着强烈的磁耦合关系。在基本尺寸计算时，如何体现转矩绕组和悬浮绕组的电磁本质，是BSRM电磁设计的关键。

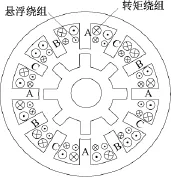
图1 12/8极BSRM的绕组结构Fig．1 Winding configuration for 12/8 BSRM

BSRM一般采用单相绕组导通控制策略，三相依次导通，并且转矩绕组电流波形一般控制为方波波形，而悬浮绕组电流为锯齿波形，因此在其主体尺寸估算时可以把两套绕组电流波形均近似为方波波形，如图2所示，其中Imp、Isp分别为主、悬浮绕组的等效方波电流峰值。

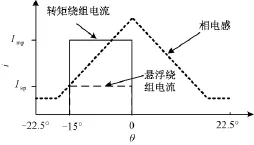
图2 BSRM一相绕组的等效方波电流Fig．2 Equivalent current for one phase winding of BSRM

设定转子处于几何中心，无径向位移。基于BSRM数学模型的推导方法［1，2，11］，考虑定、转子铁心磁路的磁压降时，一个磁极的气隙磁导Pa为:

式中，km为铁心磁压降系数;θ为转子位置角;βs为定子极弧角;δ为气隙长度;l为电机铁心长度;r为转子半径;c=1.49;μ0为真空磁导率。

此时，A相各绕组自身的电感和绕组间的互感可分别表示为:

式中，Lma为A相转矩绕组自感;Lsal、Lsa2分别为A相α、β方向悬浮绕组自感;Msma1为A相转矩绕组和α方向悬浮绕组间互感;Msma2为A相转矩绕组和β方向悬浮绕组间互感;Msa12为A相α方向悬浮绕组和β方向悬浮绕组间互感。

A相绕组的磁场储能Wa可以表示为:

式中，ima、isa1和isa2分别为A相转矩绕组电流、α方向悬浮绕组电流和β方向悬浮绕组电流;Nm为转矩绕组匝数;Nb为悬浮绕组匝数。

当α和β方向两悬浮绕组功率相等时，利用方波峰值电流表示的A相磁场储能为:

由磁场储能可得A相平均转矩Tav为:

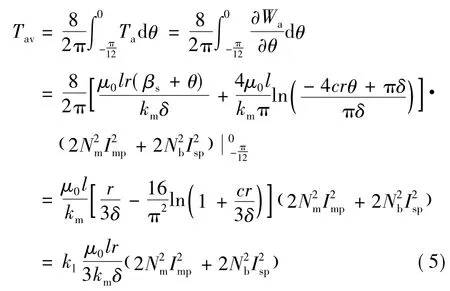
式中，kl为磁导比值系数，其表达式为:

根据平均转矩和电磁功率的关系，A相平均转矩还可以表示为:

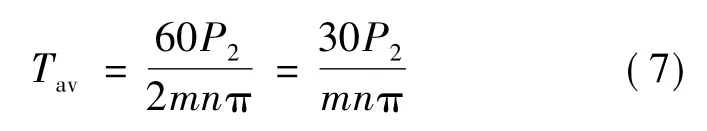
式中，P2为电磁功率;n为转速;m为相数。联合式(5)和式(7)，整理可得:

根据磁路基本定律，两套绕组磁动势与气隙磁密的关系为:

式中，Bm、Bs分别为转子处于对齐位置时主、悬浮绕组峰值电流单独产生的最大气隙磁密幅值。

由于BSRM的气隙长度相对于转子半径非常小，把式(9)代入式(8)中，整理可得12/8极BSRM的主体尺寸计算式为:

式中，D为电机定子内径。与SRM主体尺寸计算公式相比［12］，由于BSRM气隙磁场由转矩绕组和悬浮绕组磁场叠加而成，其主体尺寸计算公式中的最大气隙磁密形式为悬浮绕组磁密和转矩绕组磁密的平方和，体现了转矩绕组和悬浮绕组在基本尺寸计算中的作用。

3 绕组匝数计算

本文基于电机散热及安全运行的角度，以电机最恶劣工作状况来确定悬浮绕组额定电流值及绕组匝数。

BSRM最恶劣工作状况为每相两个方向悬浮绕组只有一个方向的悬浮绕组输出功率，而另一方向悬浮绕组无功率输出，按照此种工况来计算和确定悬浮绕组电流的有效值。

定义转矩绕组功率为Pm，悬浮绕组功率为Ps，则BSRM的输出功率P为:

一相转矩绕组峰值电流Imp和单个悬浮绕组峰值电流Isp为:

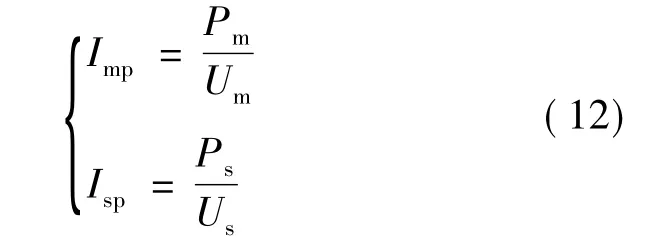
式中，Um为转矩绕组直流端电压;Us为悬浮绕组直流端电压。

转矩绕组电流的有效值Im和悬浮绕组电流的有效值Is为:

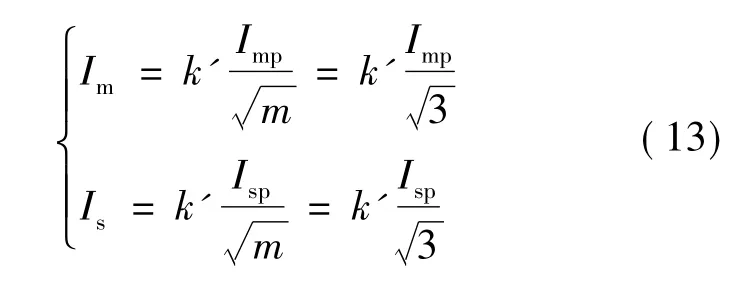
式中，k'为电流波形系数。

利用绕组峰值电流来确定绕组匝数，转子处于对齐位置处，一相四个定子齿极下的最大气隙合成磁密Bδ与主、悬浮绕组磁动势的关系为:

式中，“+”号表示悬浮绕组在该定子上起增磁作用;“－”号代表在该定子上悬浮绕组起弱磁作用。

电机结构和铁心材料确定后，最大气隙磁密Bδ可认为是一定值，主、悬浮绕组峰值电流值可由各自的功率计算得到，根据主、悬浮绕组最大气隙磁密的具体取值，式(14)中的待求量只剩主、悬浮绕组匝数。

根据主、悬浮绕组磁动势对转矩和悬浮力的影响分析可知［9］，当转矩绕组磁动势和悬浮绕磁动势相等时，即:

此时电机磁利用率最高，且产生悬浮力最大，而转矩则最小。因此设计主、悬浮绕组匝数时，在保证悬浮力输出的前提下，为提高输出转矩，主、悬浮绕组磁动势应满足:

式(16)显示，转矩绕组提供的偏置磁场大于悬浮绕组磁场，电机合成磁场中转矩绕组磁场占优，这有利于改善转矩的输出。然而，转矩绕组与悬浮绕组的磁动势相差又不能太大，从而避免因二者相差过大而造成悬浮力降低过多，进而影响电机的悬浮精度。因此，需根据电机的设计要求，合理确定主、悬浮绕组的匝数，以达到优化转矩和悬浮力特性的目的。

4 径向悬浮力计算

径向承载力是BSRM的一个重要性能指标，因为电机只有保证悬浮力输出的前提下，才能实现转子的稳定悬浮。BSRM的悬浮力属于磁阻力性质，其变化规律与绕组电感相同，幅值随电机磁路磁阻的减小而增大。因此，应根据导通区间的平均悬浮力来设计径向负载指标。

由BSRM的悬浮力方程可知，α和β方向上的位移为零时，两方向的悬浮力Fα和Fβ为:

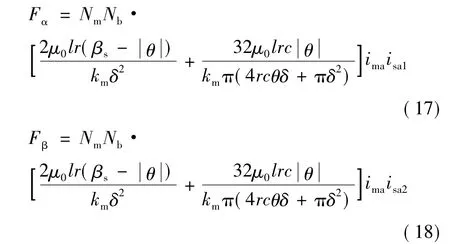
当α和β方向上的悬浮绕组电流相等时，利用峰值电流表示的总悬浮力F为:

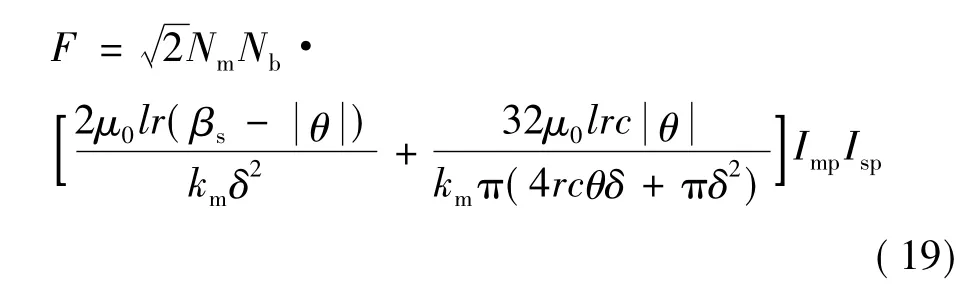
根据式(19)，可得A相平均悬浮力Fav为式(20)。

式(20)显示，悬浮力与转矩绕组和悬浮绕组磁动势的乘积成正比，同样展示了两类绕组的强磁耦合的本质。

5 定、转子极弧选取

对SRM而言，为保证电机正反两方向的起动，其定、转子极弧角应满足式(21)［13］:

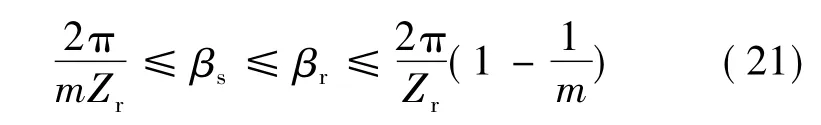
式中，βs、βr分别为定子、转子极弧角。由于BSRM结构与SRM的相似性，其定、转子极弧角也应满足式(21)。

BSRM的数学模型是根据等效磁路法推导而成，在推导过程中最关键的是气隙磁导磁路路径的选取及等效。推导中把每个定子极下的磁导由三部分磁导叠加而成，这三部分磁导分别为:定、转子齿重叠部分磁路气隙磁导P1，边缘磁路气隙磁导P2和P3

［1，2］。因此在导通区间内，定、转子极必须有重叠部分，这样数学模型的推导才成立。为此，βs、βr必须满足:

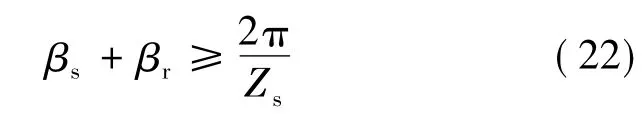
BSRM数学模型的推导中，电机定、转子极弧角通常取为相等，并且因为气隙长度相对于电机尺寸很小，可认为定子和转子的齿宽相等。定、转子极弧取值相等的好处在于:重叠部分磁路的宽度恰好为极弧角与转子位置角之差，气隙磁导P1、P2和P3始终随着转子位置角的变化而变化，这便于气隙磁导P1、P2和P3的积分求解，进而保证电感、悬浮力和转矩等电磁参数是关于电机结构参数的单值函数。

另外，BSRM由于需要对主、悬浮两套绕组电流进行控制，为简化控制方式，常把转矩绕组电流控制为方波电流形式，而对悬浮绕组电流进行实时控制。考虑到绕组电流的跟踪精度，根据电压与电感和电流的关系可知，较小的电感值有利于增大电流的变化率，缩短电流的上升和下降时间，进而提高电流跟踪精度。但电感取值较小时，又将导致相同绕组电流产生的悬浮力变小，此时需要增大电流幅值以满足悬浮力的需求。

再考虑到BSRM的两套绕组对定子槽空间要求较高的原因，BSRM定、转子极弧角通常取为式(21)下限值，即βs=βr=2π/Zs，无论这个取值是否为一个最优值。这也是12/8极BSRM的数学模型均是以定、转子极弧角为15°的情况而推导出来的原因;并且在单相控制策略下，12/8极BSRM每相导通周期角也为15°，定、转子极弧角取为15°时还有利于电机的换相。

由于BSRM本体设计的复杂性，利用本文提出的方法只能近似地估算其结构参数，并且没有考虑电机的磁饱和，因此必须借助于电磁场的有限元计算，对样机的电磁性能进行反复校核，以获得优化的电机尺寸。

6 设计实例

样机设计目标为:额定功率为2.0kW;转矩绕组额定功率为1.2kW;悬浮绕组额定功率为0.8kW;转矩绕组额定电压为110VDC;悬浮绕组额定电压为110VDC;额定转速为20000r/min;最大径向负载为100N;系统效率不小于0.75;铁心材料为35DW250;冷却方式为自然冷却;电机结构为12/8极。

6.1 主体尺寸计算

按额定工作点设计电机，对于样机有P= 2000W，n=20000r/min。对SRM而言，电机的铜损耗约占总损耗的50%，将此应用到BSRM上，其电磁功率P2可表示为:

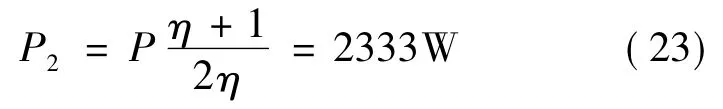
根据BSRM定子极弧选取原则，取定、转子极弧角为βs=βr=15°，气隙δ=0.25mm，转矩绕组最大气隙磁密Bm=0.8T，悬浮绕组最大气隙磁密Bs=0.8T，磁导比值系数kl=0.835，磁压降系数km=1.16，μ0= 4π×10－7H/m。将上述参数代入式(10)得:

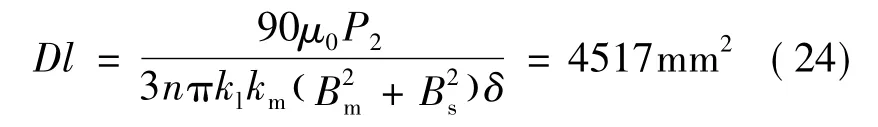
取 D=60.5mm，l=75mm，此时 Dl= 4537.5mm2，满足设计要求，叠片系数为0.94，电机铁心叠后长度为80mm。

6.2 绕组参数计算

样机一相转矩绕组由4个相对齿上的线圈串联而成，两个方向的悬浮绕组分别由两个相对齿上的线圈串联而成。每相绕组导通周期角为15°，则一相转矩绕组峰值电流Imp和悬浮绕组峰值电流Isp为:

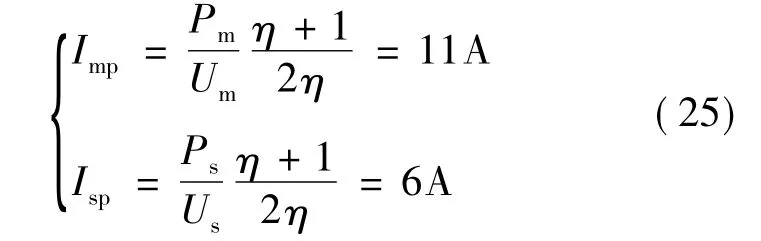
根据绕组匝数优化结论和有限元仿真，分别取转矩绕组最大气隙磁密Bm=0.8T、悬浮绕组最大气隙磁密Bs=0.65T。两套绕组的匝数为:

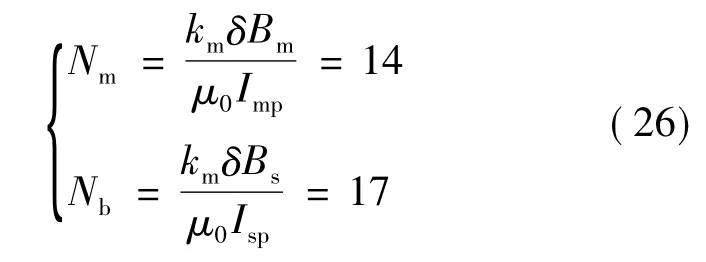
考虑电流波形系数，并计及一定的余量，主、悬浮绕组额定电流分别为:

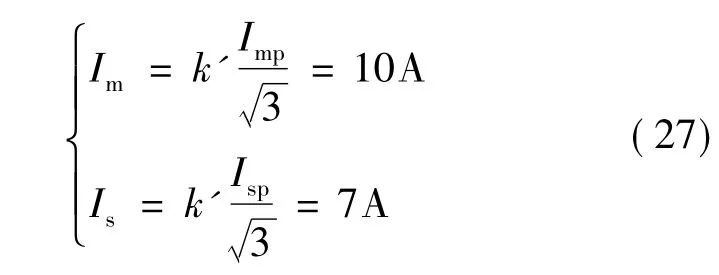
式中，k'=1.4。

电机冷却方式为自然冷却，主、悬浮绕组一个线圈电流密度为 J=6A/mm2，选取漆包线直径为0.56mm，此时主、悬浮绕组导线并绕根数分别为5根和3根。

6.3 基本尺寸计算

取定子齿高hs=24mm，根据上述尺寸，并且绕组导线按方线计算的定子槽满率为0.44。

定子极弧角βs=15°，定子齿宽ls=7.9mm，定子轭厚hz=5.75mm，定子外径Ds1=120mm，定子轭径Ds2=108.5mm，定子内径D=60.5mm。

转子外径dr=60mm，转子极弧角βr=15°，转子齿宽lr=7.9mm，转子齿高hr=8mm，转子轭厚hzr= 7mm，转子内径d3=30mm。

6.4 悬浮力计算

样机最大径向负载为100N，在确定电机的结构参数和绕组电流峰值后，可利用式(20)计算样机提供的平均悬浮力。由于绕组匝数计算时，悬浮绕组峰值电流是按最恶劣工况下计算得到的，而平均悬浮力应根据电机的额定工况来确定，此时两个方向的悬浮绕组电流相等，且为式(12)计算值的二分之一。设计样机提供的平均悬浮力为:

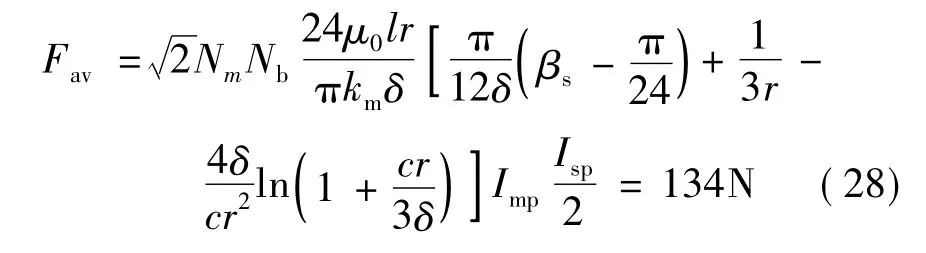
通过有限元仿真校核，得到平均悬浮力为142N，满足设计要求。

6.5 有限元验证

在计算电机结构参数时采用了一些经验取值和近似值，并且没有考虑电机的磁饱和，因此必须借助于电磁场的有限元计算，对样机的电磁性能进行校核，以获得优化的电机尺寸。为得到样机的动态电磁性能，必须借助于时步有限元分析。然而，对BSRM而言，复杂的控制系统给其性能仿真分析带来极大难度。目前，常用的电磁场有限元软件均不能对其控制系统中的位移闭环进行建模，进而不能实现其动态性能分析，因此只有通过静态场分析验证其电磁性能。

图3为基于本文设计方法研制的无轴承开关磁阻电机的原理样机，仅给出了定子和转子的叠片图。图4和图5为半个转子周期角内，A相转矩绕组电流ima=10A，isa1=0时，转矩Ta和β方向上悬浮力Fβ与转子位置角θ和β方向悬浮绕组电流isa2的变化关系。图5显示，有效导通区间(－15°～0)内，样机的转矩和悬浮力输出均能满足设计要求。

图3 样机定子和转子实物图Fig．3 Photos of stator and rotor for prototype

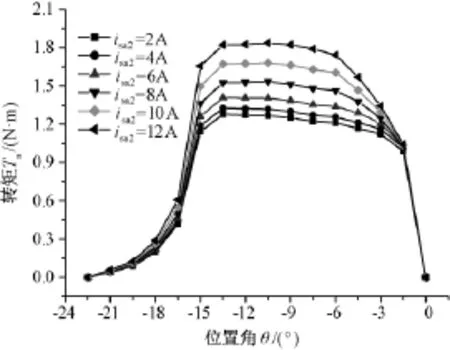
图4 转矩有限元仿真结果Fig．4 Simulated results of torque by finite element analysis

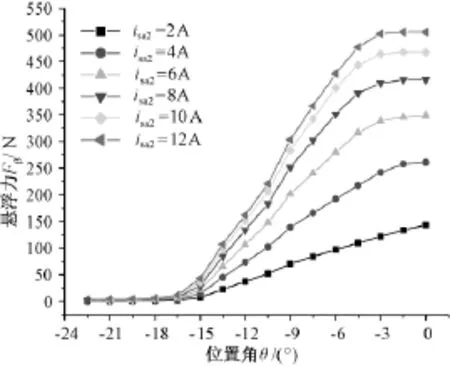
图5 悬浮力有限元仿真结果Fig．5 Simulated results of radial force by finite element analysis

7 结论

本文提出了一种12/8极无轴承开关磁阻电机的电磁设计方法，并以此设计了一台样机。得出如下结论:

(1)给出了同时计及磁耦合特性的主体尺寸计算公式，与传统电机相比，该计算公式同时考虑了主、悬浮绕组对气隙磁场的贡献。

(2)以一相绕组导通周期内的平均悬浮力作为BSRM径向悬浮力设计指标，其与利用峰值电流表示的主、悬浮绕组磁动势的乘积成正比。

(3)基于BSRM的最恶劣工作状况，提出了基于绕组峰值电流计算绕组匝数的方法。研究发现，为提高转矩的输出，设计时应使转矩绕组磁动势大于悬浮绕组磁动势。

(4)分析了BSRM定、转子极弧选取原则，为便于电机的悬浮控制和其数学模型的推导，12/8极BSRM的定、转子极弧角通常取为15°。

［1］M Takemoto，A Chiba，T Fukao．A method of determining advanced angle of square-wave currents in a bearingless switched motor［J］．IEEE Transactions on Industry Application，2001，37(6):1702-1709．

［2］M Takemoto，A Chiba，H Akagi，et al．Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation［J］．IEEE Transactions on Industry Application，2004，40(1):103-112．

［3］Cao Xin，Deng Zhiquan．A full-period generating mode for bearingless switched reluctance generator［J］．IEEE Transactions on Applied Superconductivity，2010，20 (3):1072-1076．

［4］Cao Xin，Deng Zhiquan，Yang Gang，et al．Independent control of average torque and radial force in bearingless switched-reluctance motors with hybrid excitations［J］．IEEE Transactions on Power Electronics，2009，24(5): 1376-1385．

［5］杨钢，邓智泉，曹鑫，等(Yang Gang，Deng Zhiquan，Cao Xin，et al．)．无轴承开关磁阻电机平均悬浮力控制策略 (Control strategy of average levitated force of a bearingless switched reluctance motor)［J］．航空学报(Acta Aeronautica et Astronautica Sinica)，2009，30 (3):505-511．

［6］邓智泉，杨钢，张媛，等 (Deng Zhiquan，Yang Gang，Zhang Yuan，et al．)．一种新型的无轴承开关磁阻电机数学模型 (An innovative mathematical model for a bearingless switched reluctance motor)［J］．中国电机工程学报 (Proceedings of the CSEE)，2005，25(9): 139-146．

［7］曹鑫，邓智泉，杨钢，等 (Cao Xin，Deng Zhiquan，Yang Gang，et al．)．新型无轴承开关磁阻电机双相导通数学模型 (Novel mathematical model of bearingless switched reluctance motors with two phase excitation) ［J］．电工技术学报(Transactions of China Electrotechnical Society)，2006，21(4):50-56．

［8］杨钢，邓智泉，曹鑫，等 (Yang Gang，Deng Zhiquan，Cao Xin，et al．)．适用于无轴承开关磁阻电机的功率变换器设计 (Design of power converters applied to bearingless switched reluctance motors)［J］．航空学报(Acta Aeronautica et Astronautica Sinica)，2008，29 (1):110-116．

［9］Yang Gang，Deng Zhiquan，Cao Xin，et al．Optimal winding arrangements of a bearingless switched reluctance motor［J］．IEEE Transactions on Power Electronics，2008，23(6):3056-3066．

［10］刘泽远，邓智泉，曹鑫，等 (Liu Zeyuan，Deng Zhiquan，Cao Xin，et al．)．全周期无轴承开关磁阻发电机的设计 (Design of a full-period bearingless switched reluctance generator)［J］．中国电机工程学报(Proceedings of the CSEE)，2011，31(12):77-83．

［11］刘泽远(Liu Zeyuan)．无轴承开关磁阻电机的电磁基础研究 (The basis research on electromagnetic basis of bearingless switched reluctance motors)［D］．南京:南京航空航天大学 (Nanjing:Nanjing University of Aeronautics and Astronautics)，2010.38-66．

［12］周强(Zhou Qiang)．高速开关磁阻电机的关键技术研究与实践 (The research and practice on key techniques of high speed switched reluctance machine)［D］．南京:南京航空航天大学 (Nanjing:Nanjing University of Aeronautics and Astronautics)，2009.24-28．

［13］吴建华 (Wu Jianhua)．开关磁阻电机设计与应用(Design and application of switched reluctance motor)［M］．北京:机械工业出版社(Beijing:China Machine Press)，2000.119-124．

Electromagnetic design of bearingless switched reluctance motors considering coupled characteristics of magnetic field

LIU Ze-yuan，YANG Yan
(Nanjing University of Posts and Telecommunications，Nanjing 210023，China)

Combining the derivation of mathematical model of BSRM and its operating characteristics，the computational formula of main dimension for 12/8 BSRM is proposed combining the relationship between electromagnetic torque and output power，and it can consider the coupled magnetic-field characteristics of torque winding and radial force winding．Moreover，considering the radial force characteristics of BSRM，the average radial force is used for the design of the radial load．Based on the worst operation condition of BSRM，its number of turns is calculated using the winding peak current．Moreover，the principle of selecting pole arcs of stator and rotor teeth for BSRM is analyzed．Finally，a prototype is designed using this method．

bearingless switched reluctance motor;motor design;torque;radial force

TM352

A

1003-3076(2015)10-0044-07

2014-09-16

国家自然科学基金 (51207073)、南京邮电大学引进人才科研启动基金(NY214171)和校级科研基金(NY214074)资助项目

刘泽远(1981-)，男，河南籍，讲师，博士，从事电机设计、电磁场数值分析及无轴承开关磁阻电机等方面的研究;杨 艳(1976-)，女，甘肃籍，讲师，博士，从事无轴承开关磁阻电机的振动和噪声方面的研究。