考虑保护重要度的环网最优断点集计算方法

张晓辉，常岩科，卢志刚

(1．河北省电力电子节能与传动控制重点实验室，燕山大学，河北秦皇岛066004; 2．国网藁城市供电公司，河北石家庄052160)

考虑保护重要度的环网最优断点集计算方法

张晓辉1，常岩科2，卢志刚1

(1．河北省电力电子节能与传动控制重点实验室，燕山大学，河北秦皇岛066004; 2．国网藁城市供电公司，河北石家庄052160)

在环网保护整定计算中，最小断点集的求取是关键步骤之一。考虑到不同最小断点集间存在的差异，引入了保护重要度评估指标作为断点集的评判依据，对量子离散粒子群算法进行了改进，建立了求取最优断点集的目标函数，提出了一种最优断点集的计算方法。该方法综合考虑保护风险度、保护后备依赖度和节点重要度，较为全面地评估了断点保护的重要性，同时基于改进量子离散粒子群算法具有较强寻优能力的特点，确保求得的断点集基数最小且保护重要度最低。算例仿真分析验证了本文所提方法的有效性。

最小断点集;量子离散粒子群;保护重要度;效用函数

1 引言

随着经济的快速发展，电力系统的规模不断扩大，对供电可靠性的要求也越来越高。由于环网供电有许多优点，可以避免辐射型电网单一电源供电的缺陷，提高了供电的质量和可靠性，因此，现有的输电网形成了大规模的环网。在环网中，保护之间的配合关系比较复杂，处于同一环路中的保护相互依赖、彼此配合，给保护整定计算带来一些困难。对于环网方向保护的整定，首先要确定整定的起点，即能使环网所有有向回路解环成辐射型网络的点，然后进行保护的配合整定。因此，确定整定的起点，即断点［1］，是保护整定计算的关键步骤之一。断点处的保护通常不与其他保护配合整定，故障发生时保护的可靠性相对较低，使断点成为整个电网的一个脆弱环节。

最小断点集(Minimum Break Point Set，MBPS)问题是典型的非确定性多项式完全问题，现有的求解方法主要有图论法、保护依赖函数法和人工智能算法。文献［1-4］应用图论知识首先确定电网的所有简单回路，然后利用布尔法求解MBPS，其算法具有指数复杂性。文献［5-7］通过确定保护配合关系求取MBPS，虽然省去了求解基本回路的环节，计算量较小，但是每次计算只能得到一组断点集，当电网规模较大时，不能保证所得断点集的基数最小。文献［8-11］在求出电网的基本回路后，采用人工神经网络、遗传算法等优化算法求解MBPS，但求解目标较单一，并且算法较易陷入局部最优解。通常MBPS往往不止一组，优解和劣解均混在一起，需要选择一组合适的解。在实际工作中，如何从中求出最优的MBPS作为整定的起点，避免人工随机选取的盲目性，是亟待解决的问题。

本文提出了一种考虑保护重要度的最优断点集的计算方法。应用改进的量子离散粒子群(Quantum-inspired Binary Particle Swarm Optimization，QBPSO)算法求解最优断点集。该算法基于QBPSO具有并行性、易于跳出局部最优解的本身特性，同时引入初始解筛选、禁忌表和粒子局部变异策略，提高了算法的效率。此外，该方法综合考虑了保护的风险度和保护间的本身结构特性，以及保护所在节点的重要度，使求出的MBPS达到最优。算例仿真验证了本文算法的有效性和实用性。

2 保护的重要度评估指标

依据保护配合逐级整定的原则，在环网方向保护的整定过程中，断点作为起始点，其保护定值通常不按与其相邻的保护配合整定，整定的时限也只能选择最低时限，因此断点处保护动作选择性的可靠度相对较低，成为系统中的脆弱环节［12］。当发生故障时，断点处的保护可能发生不正确动作，若重要节点处的保护发生拒动故障，则将对系统的安全稳定运行产生影响。因此，在保护整定时应尽量将断点选在保护重要度较低的位置，降低断点的脆弱性对系统的影响程度，提高系统的安全性和可靠性。断点的选取受较多因素影响，本文主要从线路断开后功率的转移状况，以及节点在网络中的重要性，来分析保护的重要度，以此衡量保护不正确动作对系统安全稳定运行影响的程度。

2.1 基于效用理论的保护风险度评估指标

效用理论［13］在经济学领域中已有很好的应用。本文类比于经济学中效用函数的定义和构成方法，将电力系统发生故障后线路潮流变化的程度作为故障的风险值。设ω为电力系统元件故障后的风险值，S(ω)为电力系统元件故障风险的效用函数，亦即潜在风险带来的不满意程度，即风险度，用S(ω)表示故障的风险度。根据电力系统运行的特点，S(ω)应满足如图1所示特性。

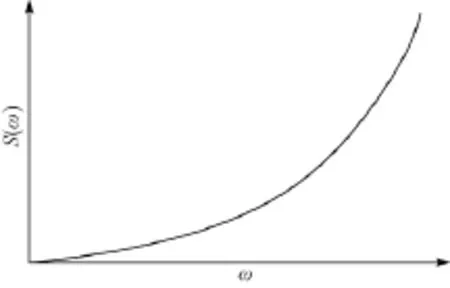
图1 故障风险度效用函数Fig．1 Utility function of evaluating fault risk

从图1中的曲线可以看出，故障的风险度随着风险值的增加而增加，且其增加速度逐渐变快，这体现了系统运行人员对故障严重程度的心理承受能力。所以本文选取风险偏好型效用函数，即S(ω)满足:在此，取

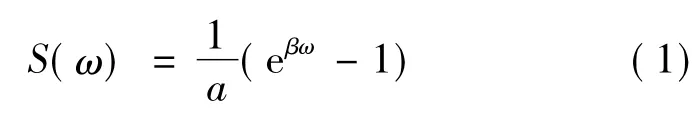
式中，α、β为常数。

假设某条线路断开，则断开线路原有的传输功率将向其他线路转移，正常运行线路的传输的功率发生变化。现有电网一般都符合N-1校验，在某条线路断开的状况下能够继续运行，但系统运行的风险会相应增加。本文应用效用函数，以故障后正常运行线路传输功率变化率的效用函数值，来量化某条线路断开的风险度，即

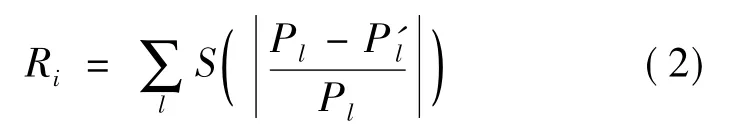
式中，Ri为线路i故障的风险度;l为除线路i的任意一条线路;Pl和P'l分别为线路l故障前后的传输功率。

将线路断开后潮流转移的风险度作为该线路的权重，定义功率传输风险度Ci，即

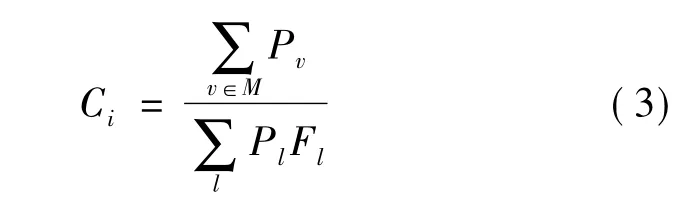
式中，M为负荷节点的集合;Pv为负荷节点v吸收的功率;l为除线路i的任意一条线路;Pl为线路l的传输功率;Fl为线路l的风险度权重。

式(3)的意义为衡量事故发生后系统的输电能力的风险度。若事故的发生导致线路传输能力的风险度变大，表明故障后其他线路为承担故障线路原本的传输任务，使系统中的功率较大范围地转移，功率传输的距离变长，网络结构对功率传输的便利性变差，输电效率降低，传输风险性变大。因此，功率传输风险度能较好地评估故障发生后电网传输能力的风险性。

若线路断开是由于线路两端保护误动作引起的，则可以用上述两评估指标评估保护误动作对系统的影响程度。为避免数量级的差异，本文用式(5)所示的归一化函数进行处理后合并在一起，定义保护风险度为

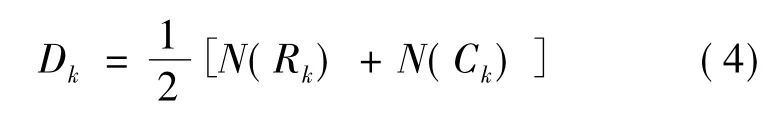
式中，Dk为保护k的风险度;Rk为保护k误动作造成所在线路断开的风险度;Ck为保护k误动作造成的功率传输风险度。

归一化函数为

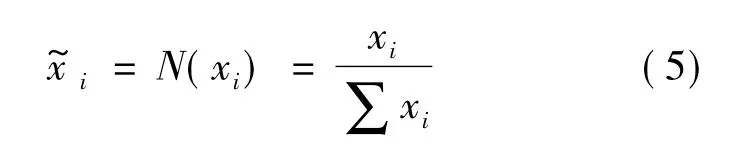
2.2 保护后备依赖度评估指标

保护间固有的主/后备配合关系在一定程度上反映了保护所在网络的结构特征。保护k的后备保护个数越多，说明其他保护对保护k的配合依赖程度越大，则保护k在电网中所处的位置电气耦合越紧密。因此，基于保护的配合后备依赖关系［5］定义了保护后备依赖度(Backup Dependency，BD)，为便于对比对其进行归一化处理，即

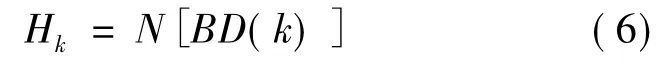
式中，BD(k)为保护k的配合后备依赖度，即保护k的后备保护的个数。

2.3 节点重要度评估指标

节点是电网的重要组成部分。网络中的有些节点具有较高的重要度，若这些重要节点出现故障，则会直接影响整个网络的连通性，同时系统运行状态也会对节点重要度产生影响。节点度数表征了节点在电网结构中与其他节点相连的紧密度，一定程度上反映了节点的重要程度。同时节点又是用电与输电的交汇点，注入节点的功率大小，说明了此节点在系统运行中的重要度。

为了消除不同量纲的影响，本文将相对节点度数与相对注入功率分别归一化后相加，作为评估节点重要度的指标，即

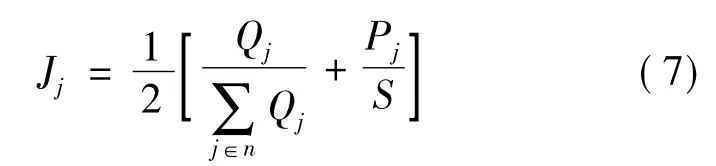
式中，Qj为节点j度数;n为节点个数;Pj为节点注入功率;S为系统注入的总功率。

2.4 保护重要度评估指标

为评估保护在系统中安装处的重要程度，本文综合考虑保护风险度、保护后备依赖度和节点重要度对保护重要性的影响，定义保护k的重要度为

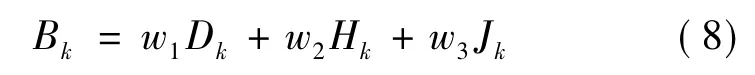
式中，Jk为节点重要度映射到保护k的重要度，取Jk为保护所在节点的节点重要度;w1、w2、w3分别为各项的权重系数，且满足w1+w2+w3=1。

由式(8)可以看出，保护重要度综合考虑了保护风险度、保护后备依赖度和节点重要度评估指标，它将系统运行状态、保护间依赖关系以及网络节点固有的结构特性对保护的影响加以综合考虑，弱化了单一评价指标的片面性，较为全面地评估了保护在网络中的重要度。依据保护重要度评估指标，选取重要度较小的保护作为断点，降低保护不正确动作对系统的影响，提高系统故障时运行的稳定性。

3 最优MBPS问题求解的数学模型

断点集是指将母线节点处的保护断开，使环网中的所有有向回路均变成开路，环网成为辐射型网络的一组保护集合。为降低断点对整定的影响，客观上要求断点的数目越少越好，所以最优的断点集，需满足保护集合基数最小，即最小断点集。以电网各母线作为节点，各方向保护为有向边构成有向图，那么MBPS的求取可等价为求解电网有向图的最小反馈边集问题［1］。

利用广度优先搜索法形成环网所有有向简单回路矩阵L，矩阵L的每一行表示一个有向简单回路。在矩阵L中，若Lij=1，则表示保护存在于第i个回路中，否则Lij=0。设元素为0或1的n维向量X=［x1，x2，x3，…，xn］，若保护rj属于断点集，则xj= 1，否则xj=0。

同时，断点也是系统的脆弱环节，为尽量使系统的脆弱性最小，需选择重要性较小的保护作为断点。所以，最优的断点集也需要满足断点保护的重要度最小。为满足上述要求，本文求解最优MBPS的目标函数和约束条件为

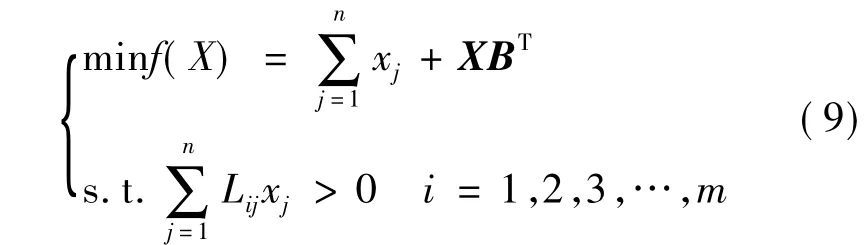
式中，X为保护状态向量;B为保护综合重要度向量;m为有向回路数目。

4 基于改进量子离散粒子群的最优MBPS求解

4.1 量子离散粒子群算法及其改进

传统的离散粒子群算法(Binary Particle Swarm Optimization，BPSO)中粒子更新自己速度v和位置x的公式如下:

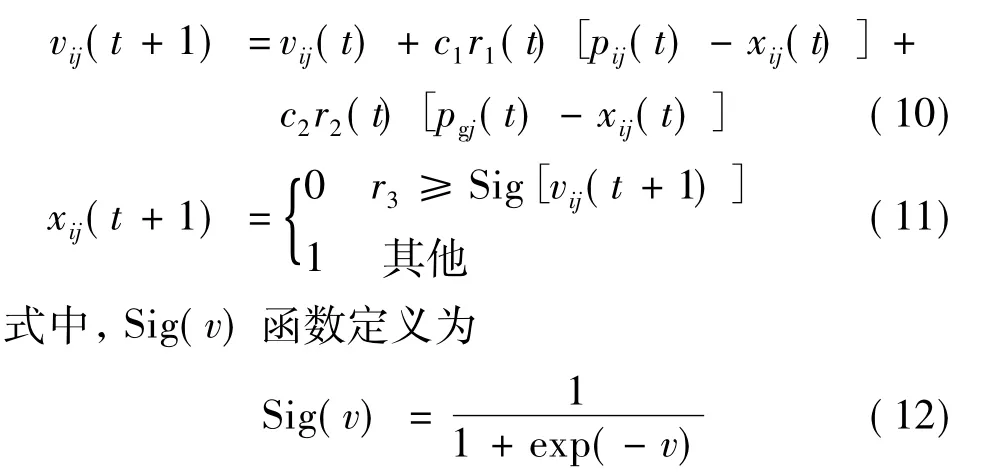
下标i表示粒子i;j表示粒子的第j维;t表示迭代次数;pi、pg为粒子的个体极值和全局极值;c1、c2为加速常数;r1、r2为两个在(0，1)之间满足均匀分布的随机数。

量子比特位［14］是量子信息的最小单元，它不但可以处于0态或1态，还可以处于两者的线性叠加态，其状态ψ可表示为

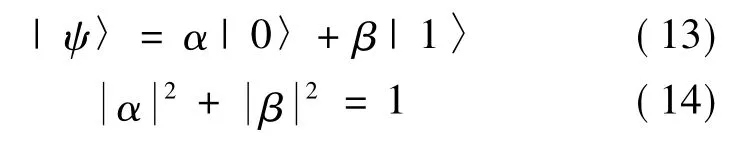
在基本的量子计算中用α、β概率复数表示1个量子比特位的状态值，这样可以表征多个状态组合的叠加，使群体具有很好的多样性，扩展了种群的数量。具有m个量子比特位的个体可以描述为:

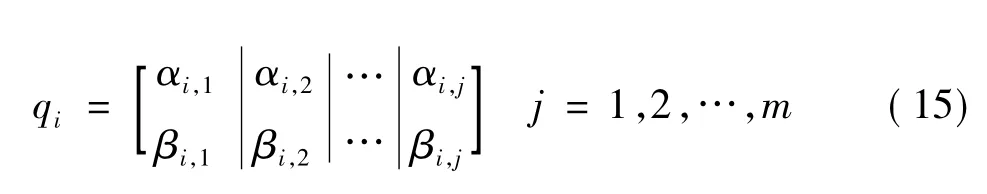
量子比特位的更新通过量子门，常用的一个量子门是旋转门［15］，如图2所示，对应表达式为

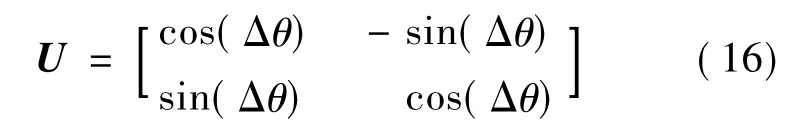
式中，Δθ为旋转角度。

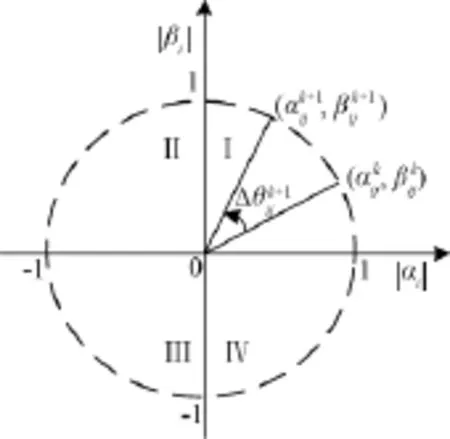
图2 量子旋转门示意图Fig．2 Diagram of quantum rotating gate

量子离散粒子群采用量子比特位编码，模拟量子坍塌的随机观察来产生粒子位置向量，不断搜索未知空间，以提高粒子群的种群多样性。粒子的速度更新公式被通过量子旋转门更新量子比特位代替，该式沿用了基本粒子群进化策略，通过统计迭代过程中粒子的个体历史最优值和全局最优值来不断引导更新量子旋转角，旋转角的幅值采用线性变化的过程，以加快算法的收敛速度。因此，QBPSO融合了量子理论和经典粒子群的优点，具有较好的种群多样性、较快的收敛速度和全局寻优的能力。

为提高量子离散粒子群算法的运行效率，同时使其更适于求取MBPS，对量子离散粒子群算法作如下改进:

(1)初始解的优化

由于初始解的生成具有盲目性，大量不符合基本约束条件的解混在初始解中，这样会直接影响到算法的运行时间。因此，首先对初始解进行优化筛选，可以提高运算速度。

(2)引入禁忌表

通过引入禁忌表，减少粒子迂回搜索次数。禁忌表通过灵活的存储结构，将迭代过程中产生的相对最优解存储在禁忌表中。在迭代一定次数后，下次迭代时，首先判断此解是否存在禁忌表中，以此来减少迂回搜索的次数，提高运行效率。

(3)局部变异策略

量子离散粒子群算法在迭代的后期也易陷入局部最优解，出现早熟现象。根据断点集的特性，次优解粒子中一定含有多余的保护，通过对次优解中所包含的某保护进行移除操作，可以使次优解进一步接近最优解。本文模拟遗传算法中基因变异，对迭代到一定次数的次优解粒子进行变异操作。由于QBPSO算法一般在迭代后期出现收敛缓慢，所以本文在迭代次数进行到一半时，引入局部变异策略。局部变异策略可以用图3表示。

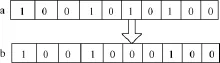
图3 局部变异策略示意图Fig．3 Diagram of partially mutation strategy

4.2 最优MBPS问题的求解

量子粒子群算法是一种智能优化算法，依据目标函数不断调整搜索个体历史最优值和全局最优值的策略来不断引导更新量子旋转角，最终找到全局最优解。

将保护状态向量Xi=［xi1，xi2，xi3，…，xin］作为可行解，表示粒子i的位置。当xij=1时表示粒子i认为保护j属于MBPS，否则xij=0时保护j不属于MBPS。

基于改进QBPSO的最优MBPS求解步骤如下。

(1)初始化量子比特位，量子的向量位置按式(17)生成，得到初始粒子，每一个粒子对应一组断点集。对每个粒子按式(9)的基本约束条件进行筛选，舍去不满足约束条件的粒子，并重新产生符合条件的粒子。式中，i=1，2，…，N;j=1，2，…，m;ri，j为0和1之间的均匀随机数;N为种群大小;m为粒子维数。

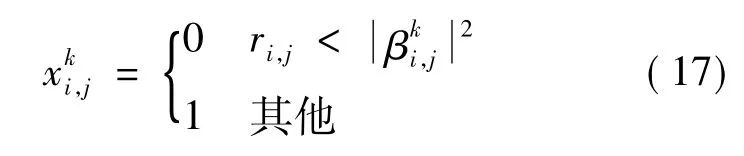
(2)根据本文的目标函数计算种群中所有粒子的适应值。对每个粒子i，将其目标函数值与其历史最优目标函数值进行比较，取最优者为个体极值比较每个粒子的个体极值，找出最优者作为全局最优值本文取目标函数越小越接近最优解。

(3)通过式(18)来更新量子比特位，采用式(17)更新粒子的向量位置。

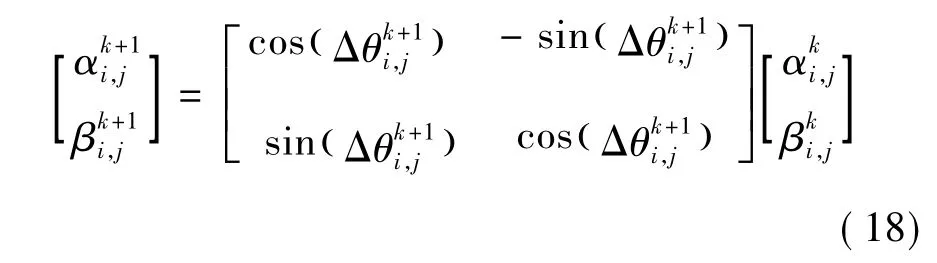
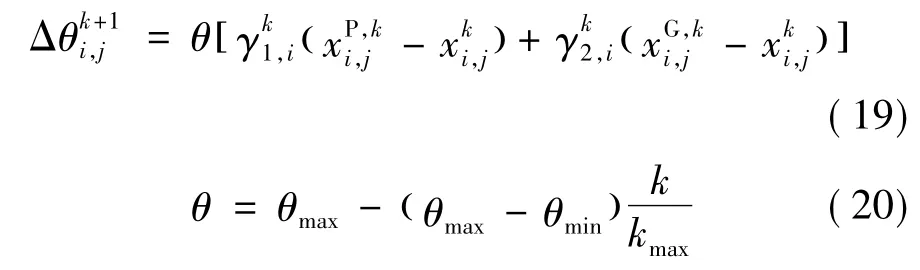
式中，θmax、θmin分别为旋转角幅值的最大、最小值，θ一般取弧度为0.001π～0.05π;kmax为 QBPSO最大的迭代次数;k为当前的迭代次数;通过比较粒子当前位置的适应度值和个体极值以及全局极值的大小，来确定是否引导调整量子旋转角，即

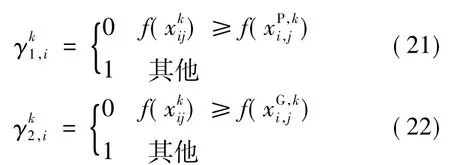
(4)判断满足一定迭代次数(总迭代次数的一半)后，对禁忌表中的粒子进行局部变异策略生成下一代粒子。

(5)判断满足一定迭代次数(设定为10)粒子是否在禁忌表中，若在，转到步骤(3);反之，进行步骤(6)。

(7)如果达到最大迭代次数，则停止计算;否则，转到步骤(3)。

5 算例分析

本文采用如图4所示的典型多环网算例图。图中包含5个节点、7条线路和14个保护，各元件参数均采用标幺值表示，选择基准容量SB=100MVA，基准电压UB=110kV。

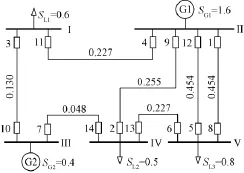
图4 某系统网络连接图Fig．4 Connection diagram of system network

各评价指标的求解步骤如下。

(1)对全网进行潮流计算，求出正常运行时各线路传输的功率。断开某条线路后，对节点导纳矩阵参数进行相应的修改，再进行潮流计算，得到某条线路退出运行后，其余各线路的传输功率。遍历所有线路，然后根据式(4)求得各保护的风险度。

(2)根据保护配合关系，可以求出各保护的后备保护数目，进而依据式(6)得到保护的后备依赖度。

(3)由网络图可以求出各节点的度数，从正常运行的全网潮流计算结果得到各节点的注入的功率，根据式(7)计算出节点的重要度。

(4)根据式(8)保护重要度的定义，假设保护风险度、保护后备依赖度和节点重要度对保护重要性的影响程度相同，即取三个指标的权重系数相等时，计算出保护重要度。

各指标计算结果如表1所示。表1列出了保护的各项评估指标数据。可以看出，本文提出的保护风险度、保护后备依赖度和节点重要度指标能较好地辨识保护重要度的差异。如保护11，其保护后备依赖度为0.0714，所在节点的重要度为0.2293，与其他保护相比较小，但其保护风险度为0.3192较大，使其保护综合重要度达到0.2066也较大;保护11的保护风险度较大，表明若它断开将导致线路潮流在系统中较大转移，引起连锁故障的可能性也大。又如保护1和12保护风险度都为0.1334均较小，但保护相对后备依赖度为0.2143，保护所在节点重要度为0.5376，均较大，因而其保护重要度也比较大。由此可见，相对于单一指标的选取方法，考虑了多方面指标的保护重要度有效克服了考察角度单一的弊端。

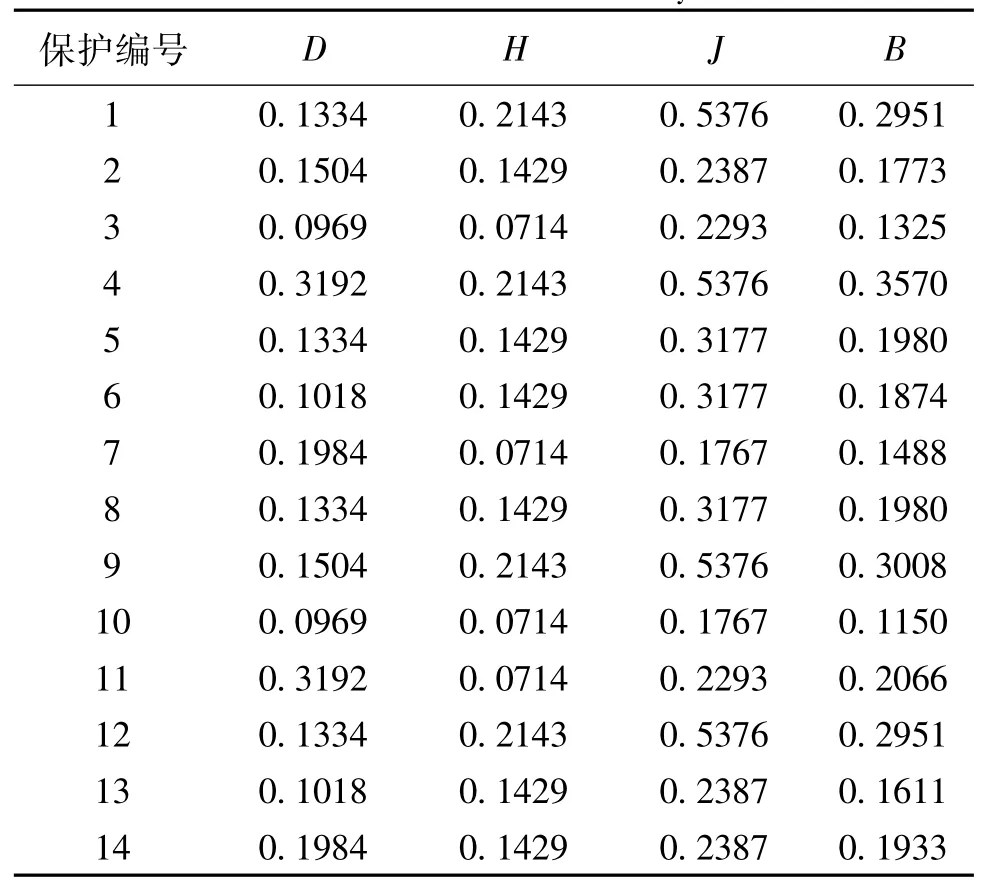
表1 保护各项评估指标Tab．1 Indicators of relay

建立算例图的所有有向简单回路矩阵L:

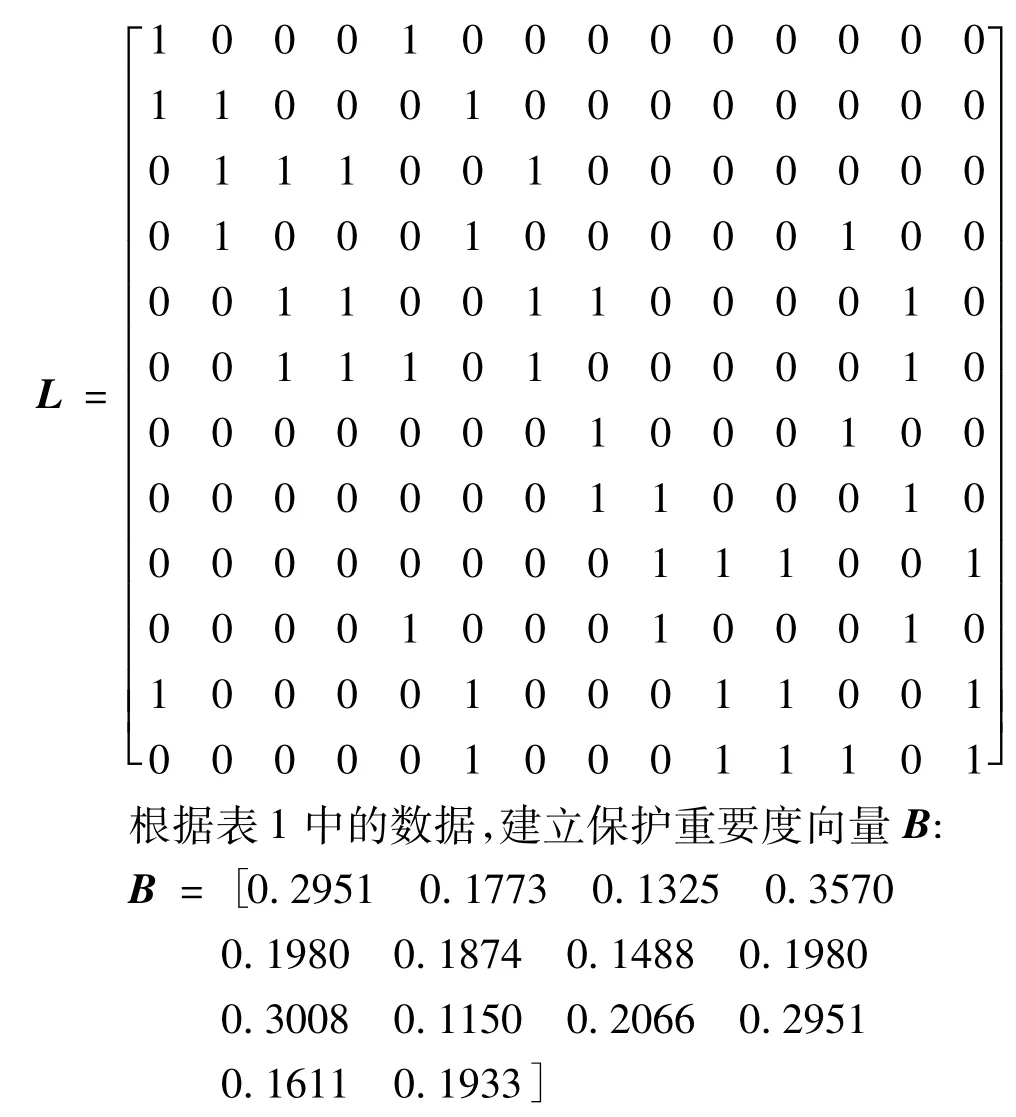
本文设置种群规模为200，迭代次数为100次，运用Matlab编程进行仿真分析。

在各指标权重系数w1、w2、w3相等的条件下，本文进行了5次独立的计算过程，其结果均相同，最优断点集为{2、5、8、10}，适应值为4.6883。计算结束后，从禁忌表中可以得出满足最小断点集基本约束条件，但不是最优断点集的解包含{1、3、9、12}、{1、4、9、12}、{1、7、9、12}、{2、5、8、11}、{2、5、8、14}，它们的适应值分别为5.0235、5.2480、5.0398、4.7799、4.7666，均大于最优断点集的适应值。这些解涵盖了算例中所有的最小断点集，可以看出本文的方法在确保最小断点集多样性的前提下，求解出最优的断点集{2、5、8、10}。从求出的最优断点集可以看出，不含有保护1、保护4等重要保护。可见，保护重要度从不同的角度描述了保护的重要性，提升了对保护重要性的辨识效果，使求解出的最优断点集可信度更高。

在不同的权重系数下，得出的最优断点集可能存在差异，所以在工程应用中可根据实际情况的侧重点，设定各指标的权重系数，以使选出的最小断点集达到最优。

6 结论

本文提出了一种基于改进的量子离散粒子群算法求解最优断点集的方法。该方法利用QBPSO具有易于突破局部最优值的寻优机制，考虑了最小断点集求取的特点，同时引入保护重要度评估指标作为断点集寻优的评判依据，可以在含有多组同基最小断点集的情况下，求出一组相对最优的断点集。本文所提方法能够在不同条件下满足断点集选择的要求，灵活地适应工程应用。通过算例仿真分析验证了本文方法的可行性。

［1］Bapeswarar V V，Sankarar K．Computer aided coordination of directional relays:Determination of break points ［J］．IEEE Transactions on Power Delivery，1988，3 (2):545-548．

［2］言昭(Yan Zhao)．应用图论优化复杂环网继电保护整定配合的简便算法 (An application of graph theory for optimal coordination of transmission protection system in multi-loop network)［J］．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，1989，1(1):80-86．

［3］Prasad V C，Prakasa Rao K S，Subba Rao A．Coordination of directional relays without generating all circuits ［J］．IEEE Transactions on Power Delivery，1991，6 (2):584-590．

［4］李银红，段献忠(Li Yinhong，Duan Xianzhong)．继电保护整定计算中形成简单回路的方法 (Study on the simple loop formation method in relay coordination)［J］．中国电机工程学报 (Proceedings of the CSEE)，2003，23(2):20-25．

［5］吕飞鹏(Lv Feipeng)．基于配合关系计算复杂环网保护最优配合顺序的新方法(A novel method for determining the optimal coordination sequence of directional relays in a complicated multi-loop power networks based on coordination relationships of relays)［J］．电力系统自动化 (Automation of Electric Power Systems)，2005，29 (24):65-69．

［6］马静，叶东华，王彤，等 (Ma Jing，Ye Donghua，Wang Tong，et al．)．电力系统多区域复杂环网的最小断点集计算(Calculation of minimum break point set for multi-area complex loop network of power system)［J］．中国电机工程学报 (Proceedings of the CSEE)，2011，31(28):104-111．

［7］刘丹，吕飞鹏(Liu Dan，Lv Feipeng)．基于网络化简和配合关系的最小断点集计算方法 (A novel method for determining minimum break point set based on network graph simplification and coordination relationships of relays)［J］．电力系统自动化 (Automation of Electric Power Systems)，2008，32(16):24-27．

［8］吕飞鹏，米麟书，姜可熏 (Lv Feipeng，Mi Linshu，Jiang Kexun)．环网方向保护配合最小断点集的神经计算方法 (Neutral approach to determine minimum break point set for optimal coordination of directional protective relays in multiloop networks)［J］．中国电机工程学报 (Proceedings of the CSEE)，1997，17(3): 41-46．

［9］Sharifian H，Abyaneh H A，Salman S K，et al．Determination of the minimum break point set using expert system and genetic algorithm［J］．IEEE Transactions on Power Delivery，2010，25(3):1284-1295．

［10］陈绩，吕飞鹏，黄姝雅 (Chen Ji，Lv Feipeng，Huang Shuya)．确定复杂环网方向保护最小断点集的改进离散粒子群优化算法 (An improved discrete particle swarm optimization algorithm to determine minimum break point set of directional protection for multi-loop network) ［J］．电网技术(Power System Technology)，2008，32 (12):90-94．

［11］刘丹，吕飞鹏(Liu Dan，Lv Feipeng)．基于蚁群算法的环网方向保护配合最小断点集计算(Ant colony optimization algorithm based determination ofminimum break point set for coordination of directional protective relay in multi-loop networks)［J］．电力系统自动化(Automation of Electric Power Systems)，2008，32 (21):27-31．

［12］李运坤，吕飞鹏，陈新，等 (Li Yunkun，Lv Feipeng，Chen Xin，et al．)．基于节点重要度估计的多组同基最小断点集选取方法 (A method for selecting a minimum break point set(MBPS)from multi-MBPS with the same cardinal number based on evaluation of node importance)［J］．电力系统自动化 (Automation of Electric Power Systems)，2010，34(12):58-60．

［13］张国华，段满银，张建华，等 (Zhang Guohua，Duan Manyin，Zhang Jianhua，et al．)．基于证据理论和效用理论的电力系统风险评估(Power system risk assessment based on the evidence theory and utility theory) ［J］．电力系统自动化 (Automation of Electric Power Systems)，2009，33(23):1-4，47．

［14］吴小删，张步涵，袁小明，等 (Wu Xiaoshan，Zhang Buhan，Yuan Xiaoming，et al．)．求解含风电场的电力系统机组组合问题的改进量子离散粒子群优化方法(Solutions to unit commitment problems in power systems with wind farms using advanced quantum-inspired binary PSO)［J］．中国电机工程学报 (Proceedings of the CSEE)，2013，33(4):45-52．

［15］Lau T W，Chung C Y，Wong K P，et al．Quantum-inspired evolutionary algorithm approach for unit commitment［J］．IEEE Transactions on Power Systems，2009，24(3):1503-1512．

Method for determining optimal break point set considering relay protection importance in multi-loop power network

ZHANG Xiao-hui1，CHANG Yan-ke2，LU Zhi-gang1
(1．Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province，Yanshan University，Qinhuangdao 066004，China;2．State Grid Gaocheng Power Supply Company，Shijiazhuang 052160，China)

Determining minimum break point set is one of the key steps of setting and calculating of relay in a multi-loop network．A method for determining the optimal break point set is proposed．To assess the difference ofminimum break point set，the concept of relay importance is introduced．The objective function can be built based on the improved quantum-inspired binary particle swarm optimization algorithm for the optimal break point set．Thus the method takes the risk and backup dependency of relay and the importance of node in system into account，and makes a comprehensive assessment of the importance of the break point set．At the same time based on strong searching ability characteristics of the improved quantum-inspired binary particle swarm optimization algorithm，the minimum base of break point set and the lowest importance of the result can be ensured．The effectiveness of the proposed method is validated with simulation analysis．

MBPS;QBPSO;relay protection importance;utility function

TM77

A

1003-3076(2015)10-0068-08

2014-10-13

张晓辉(1973-)，女，河北籍，副教授，硕士，研究方向为电力系统经济运行、电力系统继电保护等;常岩科(1987-)，男，河北籍，硕士研究生，研究方向为电力系统继电保护整定。