修正的DSmT证据编码方法

2015-05-25李鸿飞金宏斌田康生

系统工程与电子技术 2015年8期

关键词：字符解码信度

李鸿飞，金宏斌，田康生，王晶

（1.空军预警学院四系，湖北武汉430019；2.北京云星宇科技服务有限公司，北京100078）

修正的DSmT证据编码方法

李鸿飞1，金宏斌1，田康生1，王晶2

（1.空军预警学院四系，湖北武汉430019；2.北京云星宇科技服务有限公司，北京100078）

计算量是影响Dezert-Smarandache理论（DSmT）应用的重要因素之一，也一直是DSmT的研究热点。计算编码由于其证据表示和信度计算的合理性，得到了广泛的认可。计算编码在编码转换时简单有效，但在解码转换时需要进行全部可能元素查找，需要大量查找计算，降低了计算编码的执行效率。文章提出了一种修正的DSmT证据编码方法，该方法将焦元关系转换为唯一的位置属性并事前存储于数据库中，减小了在解码过程中的查找计算量，修正方法在不改变合成结果的前提下更加有效。算例也验证了修正方法在合成结果上的正确性和计算量上的高效性。

Dezert-Smarandache理论；计算量分析；证据编码；计算编码；解码变换

0 引言

Dezert-Smarandache理论（DSmT）的计算量主要产生于证据的组合过程，由于DSmT引入冲突焦元的概念，使得DSmT的计算量比DST更大［1－4］。DSmT的证据处理过程的计算量问题涉及到3个问题，一是证据的近似；二是合成规则的近似；三是证据的表示（包括证据编码和证据解码）。针对3类问题，专家学者提出3类方法。第一类方法是焦元近似方法，通过对原始证据或焦元进行简化来减小计算量，主要针对问题1，例如，Tessem的k-l-x方法［5］、基于能量函数法［6］、贝叶斯近似方法［7］、排序融合法［8］、层次比例近似方法［9］、证据控制方法［10－13］等。第二类方法是规则近似方法，针对具体应用可以将组合规则进行简化，减少不必要的计算，主要针对问题2，例如，层次假设近似方法［14］、基于树的近似方法［15－18］等。第三类方法是证据编码方法，通过使编码蕴含逻辑关系，使用编码可以有效处理焦元间并节省查找计算量，主要针对问题3，如Smarandache编码［19］、计算编码［20］。

3类方法序贯执行，可以从不同的角度减小计算量。如上节分析，目前计算量的分析主要集中于证据近似和合成规则近似，对证据编码方法的研究较少。但证据编码方法是DSmT方法可以进行计算机编程的基础，其作为证据表示的方式嵌入整个证据合成流程，在完成计算机编程的同时控制了不必要的计算量。目前，最有效的方法是文献［20］提出的计算编码。计算编码在编码转换时简单有效，但在解码转换时需要进行全部可能元素查找，需要大量的查找计算，降低了计算编码的执行效率。针对计算编码在解码变换时存在的问题，本文提出一种修正的计算编码方法。该方法分为事前处理部分和实时处理部分，将元素的位置属性与计算编码事先对应于数据库中，实时处理时只需定位合成结果的位置码，即可得到合成结果的字符编码显示输出。本方法在不影响计算编码合成有效性及编码变换简易性的同时，使得解码变换简化，提高了编码方法的效率。

1 证据编码方法

1.1 现有的证据编码方法

原始的证据通过字符表示，如目标1表示成θ1，目标1或目标2表示成θ1∪θ2，这种证据焦元的原始表示方法称为字符编码。字符编码易于理解，但不同焦元间的蕴含关系需要用户参与处理，这极大地阻碍了DSmT在计算机系统中的应用。同时字符编码每次处理需查找相应焦元及其对应的基本信度值，增加了计算量。为此，专家提出了表示编码、Smarandache编码以及计算编码，试图解决字符编码的存在问题。最直观的方法是对字符编码进行数字化，使其便于计算机处理。表示编码就是把字符编码都通过数字表示。表示编码初始数字化字符编码，但焦元间的逻辑关系还没有蕴含在编码中。同时考虑数字化和焦元逻辑，根据对焦元逻辑的不同处理方式，有文献［19］提出的Smarandache编码方法和文献［20］提出了计算编码。维恩图以图的形式表示了命题间的逻辑关系。图1（a）和图1（b）分别表示了辨识框架元素数n＝3时，命题的维恩图及其对应的Smarandache编码和计算编码。计算编码在Smarandache编码的基础上将维恩图分离部分以单个数字表示，比Smarandache编码的数字组合表示更为简单有效。

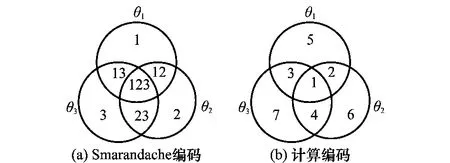
图1 命题的维恩图及其对应的两种编码（n＝3）

不同的证据编码有不同的特点，其特点又决定了其计算量和适用范围。4种证据编码在表1中进行了分析。

表1 证据编码的特点分析

1.2 计算编码存在问题

计算编码由于将焦元关系内含于编码中，可以有效降低证据焦元组合以及证据查找的计算量，并且易于编程实现，是一种有效的表示方法。其信息流程如图2所示。

图2 基于计算编程证据合成的信息流程

计算编码在编码和证据组合上简单有效，但在解码过程中，由于合成结果焦元不一定包含在原始证据焦元中，为了得到合成结果的字符编码，需要将合成结果的计算编码逐个与各元素的计算编码进行比较，且DSmT元素包含辨识框架的所有超幂集元素，在极端情况下解码所需的查找计算量甚至会超过证据合成所需的计算量。如假设证据有n个焦元，需要查找的焦元数量为m，则需要查找的计算量以平均查找次数表示，记为O查找（f（n，m））。若每个焦元拥有相同的查找概率，且查找成功和查找失败的概率相同，计算编码的查找计算量

例1 假设｜Θ｜＝4，原始证据焦元数分别为11和12，合成结果焦元数为51，则合成计算量为197.5，解码计算量达到3／4×（167＋1）×51＝6 426。

2 修正的计算编码方法

2.1 算法模型

计算编码虽然能有效完成证据的表示，但其在解码过程中的查找产生的计算量降低了其使用效率。在研究中发现，可以将计算编码中的焦元关系转换为某种代码，以减少查找的计算量。在计算编码的基础上对计算编码给出唯一的标识，使其增加新的标识属性便于查找。在不改变计算编码结构的基础上，将计算编码的唯一性信息作为新标识在数据库中与计算编码对应。将需要程序实时进行的操作，提前置于数据库中，相当于将查找操作事前进行。基于该思想，本文提出了一种修正计算编码方法，修正方法的证据处理过程如图3所示。非辨识框架元素中的操作符（与操作、或操作）数为ak（k＝1，…，n－｜Θ｜，ak＝w，w是正整数），则编码计算量为

图3 修正方法的信息流程

修正计算编码方法的处理过程分为3个步骤进行。下面对这3个步骤进行分析，并给出了3个步骤中产生的计算量。

步骤1 证据编码。证据编码分为首先查找相应辨识框架的完整计算编码，然后从输入证据的字符代码开始，到转换为表示编码，再转换为计算编码。其中证据的字符编码中单焦元的个数决定了在转换过程中所需的查找次数。例如，需要对θ1∩θ2进行证据编码，需要查找θ1和θ2的相应辨识框架的完整计算编码，然后再按照第2.1节的方法得到具体的证据编码。计算量为查找次数2。证据的字符编码在其集合的最简形式下，其交、并集的次数永远比单焦元次数多1。在不同的辨识框架下，单焦元的定义和表示不同，但交、并集的表示是一致的，因此本文以交、并集的次数来衡量编码计算量。但编码计算量的实质是查找的次数。

定义1 假设在DSm模型下，有l维辨识框架Θ＝｛θ1，θ2，…，θl｝，证据有n个焦元，其中辨识框架元素个数为｜Θ｜，

步骤2 焦元组合与信度计算。首先根据应用确定组合规则，计算焦元相交情况并进行去重，同时计算相交的基本信度值，得到合成结果。由于逻辑关系蕴含于计算编码内，合成结果的计算编码可直接组合得到，所以不考虑焦元组合计算量。在信度组合方面，证据合成可以看作乘运算（除运算）和加（减运算）两种原子操作组成。两种操作根据不同的算法产生的计算量不同，乘运算的计算量大于加运算的计算量，本文将两种操作次数加权处理得到信度组合计算量。

定义2 在DSm模型下，有n维辨识框架Θ＝｛θ1，θ2，…，θn｝，根据相应限制条件，最大可能焦元集为GΘ（GΘ表示可为不同模型），则焦元数为｜GΘ｜，对k条证据mj（Ajl）（j＝1，2，…，k；l＝1，2，…，｜GΘ｜；Ajl⊆Θ），用某种组合规则组合这k条证据所需要运算的乘法和除法的次数与加法次数的加权和称为该组合规则的信度组合计算量，表示为O组合（f（n，k））。

步骤3 证据解码。合成结果进行解码，得到字符编码表示的合成结果并显示给用户。修正的DSmT证据编码方法保持了计算编码在证据组合时优良性质，并对解码部分进行了改进，分为事先处理部分和实时处理部分（见图4）。事先处理部分即在系统设计时就将位置码加入编码数据库，这样在实时处理部分对合成结果的计算编码进行解码时，可直接通过其位置码获取合成结果的字符编码，不必进行大量的查找。这样将原来在实时处理部分进行的查找可以看做在事前进行。

图4 修正编码方法的事前处理和实时处理过程

事先处理部分首先生成不同辨识框架下所有元素的计算编码；判断编码数据库中该计算编码是否有对应的位置码，若有，则判断下一个计算编码，若无，继续运行；将计算编码的每个数字转换成为二进制码，若计算编码存在数字a，则将二进制码的第a位设置为1，其余为0，m等于最大编码数，一个计算编码对应一个m位二进制码；将二进制码转换为十进制，得到唯一的位置码，并与该计算编码对应；对所有未转换计算编码循环进行第二步到第五步，至所有元素都已完成转换。

实时处理部分与事前处理部分原理类似，但在步骤上稍有不同。实时处理部分得到组合结果首先得到其计算编码的位置码，直接在数据库中查找位置码获取对应的字符编码。首先得到合成结果的焦元计算编码；将计算编码转换为二进制码；将二进制码转换为十进制，得到位置码；在编码数据库中定位位置码，得到字符编码；字符编码与其基本信度组装，输出显示。

下面用一个例子，说明修正方法的解码过程。

例2 假设辨识框架n＝3，则其最大编码数为7，得到的合成结果计算编码为［1 2 3 5］、［1 3］、［1］，其对应的基本信度值分别为0.675 4、0.297 5和0.027 1，解码过程如图5所示。

图5 一个修正编码方法的解码过程举例图

修正方法的解码计算量是在证据由计算编码转换为字符编码过程中产生的计算量，主要为转换为位置码产生的计算量，即得到位置码后即查找相应字符编码的次数。

定义3 假设组合结果有n个焦元，则解码计算量为O解码（f（n））＝n。

2.2 总计算量的分析与比较

计算编码和修正方法的计算量都由组合计算量、编码计算量和解码计算量组合。但如果将总计算量表示为3种计算量的简单加和是不合理的。这是因为组合计算量是组合过程中乘法与加法运算的加权和，而编码计算量和解码计算量都是查找次数。组合计算量是一类计算量，编码计算量和解码计算量是一类计算量。为此，以二元组的形式分别表示两类计算量。

定义4 设在证据处理过程中，其组合计算量、编码计算量和解码计算量组合分别为O组合、O编码和O解码，则证据处理过程中产生的总计算量为O总＝［O组合，O编码＋O解码］。

根据第1节、2.1节及本节对计算量的定义，对两种方法的计算量进行定量分析。

假设有两条证据E1和E2，D为所代表的模型，辨识框架元素数为｜Θ｜，其焦元数分别为n1和n2，非辨识框架元素中的操作符数为和，组合结果焦元数为r。则计算编码方法和修正编码方法的计算量如表2所示。使用经典DSm组合规则对两条证据进行融合。两条证据的经典DSm组合其信度组合计算量为乘除操作与加操作的加权和，即n1×n2＋α（n1×n2－1），α为加操作权系数。

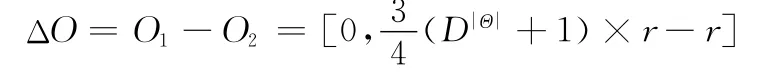
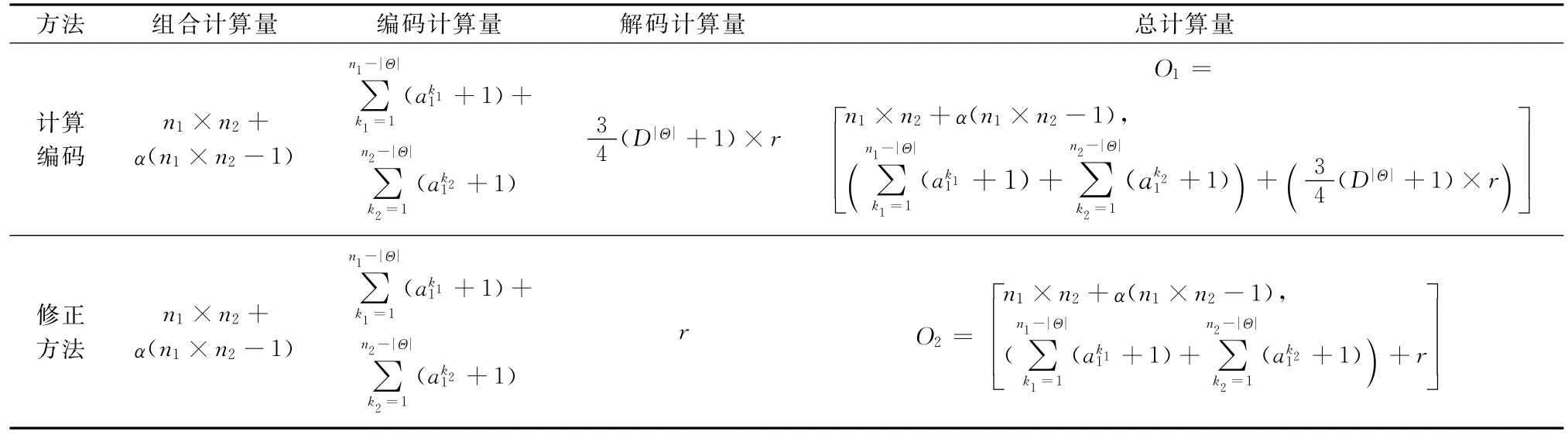
表2 计算编码与修正方法计算量比较

3 算例分析

不同类的减小计算量方法在证据处理中的应用位置不同且可以序贯使用，因此只有同类的方法比较有实际意义。仿真通过对证据编码方法中的计算编码和修正方法进行比较，验证修正计算编码方法的有效性。

仿真背景：在自由DSm模型下，辨识框架为Θ＝｛D，Z，Y，Q｝，假设在某时刻从传感器获得两组证据E1、E2，其基本信度分配值m1、m2，如表3所示。两条证据都认为是元素D。使用经典DSm组合规则对两条证据进行融合。信度组合计算量度量中α取值为0.5。

主要对两种方法的计算量和合成结果进行计算和评价。表4、表5比较了两种方法的合成结果和计算量。

两种编码的组合结果见表4。从表4中可以看出，两种方法的决策结果为D，与直觉结果一致，两种编码在组合时一致，均可以有效识别。

表3 某时刻的基本信度分配值

表4 两种编码的合成结果比较

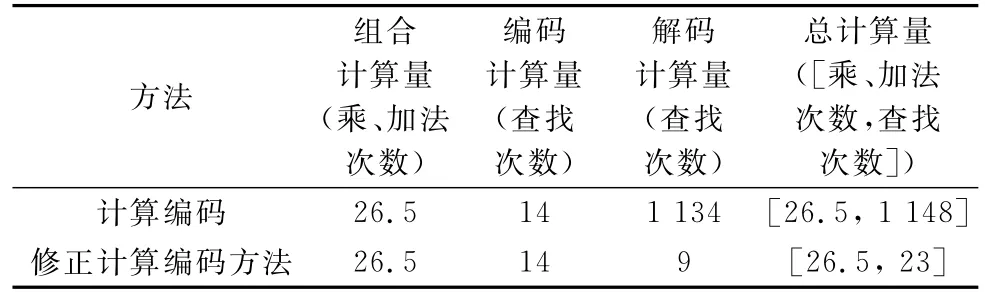
表5 两种编码的计算量比较

两种编码的计算量见表5。从表5中可以看出，修正计算编码方法的计算量明显小于计算编码，其中两种方法的组合计算量和编码计算量均相等，主要差别在于解码计算量。修正计算编码方法将计算编码需要查找才能完成的功能以位置码的形式内化于数据库中，不再需要对合成结果进行反复查找。修正计算编码方法可以看做是以“数据换程序”的思路进行的。修正计算编码方法既保持了计算编码在证据组合时的有效性和计算机编程的易用性，又深入挖掘计算编码的内在特性，使其更加合理高效。

4 结束语

本文提出了一种新的DSmT证据编码方法，该方法基于计算编码，将位置属性加入计算编码中，解决了计算编码在解码变换时计算量大的问题。修正方法的解码部分分为事前处理部分和实时处理部分，将元素的位置属性与计算编码事先对应于数据库中，实时处理时只需定位合成结果的位置码即可得到合成结果的字符编码显示输出。算例也验证了修正方法在合成结果上的正确性和计算量上的高效性。下一步，本课题组将继续研究编码的存储结构，以方便编码的查找、排序、修改，进一步提高处理效率。

［1］Destercke S，Burger T.Toward an axiomatic definition of con-flict between belief functions［J］.IEEE Trans.on Systems，Man and Cybernetics，Part B，2013，13（2）：585－596.

［2］Fu Y W，Yang W，Zhuang Z W.Review on evidence modeling［J］.Systems Engineering and Electronics，2013，35（6）：1160－1167.（付耀文，杨威，庄钊文.证据建模综述［J］.系统工程与电子技术，2013，35（6）：1160－1167.）

［3］Dezert J.An introduction to DSmT for information fusion［J］.New mathematics and Natural Computation，2012，8（3）：343－359.

［4］Smarandache F，Dezert J.On the consistency of PCR6with the averaging rule and its application to probability estimation［C］∥Proc.of the 16th International Conference on Information Fusion，2013：1119－1126.

［5］Tessem B.Approximations for efficient computation in the theory of evidence［J］.Artificial Intelligence，1993，61（2）：315－329.

［6］Ye Q，Wu X P，Zhai D J.Combination algorithm for evidence theory utilizing energy function［J］.Systems Engineering and Electronics，2010，32（3）：566－569.（叶清，吴晓平，翟定军.一种基于能量函数的证据合成算法［J］.系统工程与电子技术，2010，32（3）：566－569.）

［7］Voorbraak F.A computationally efficient approximation of Dempster-Shafer theory［J］.International Journal of Man-Machine Studies，1989，30：525－536.

［8］Yang Y，Han D Q，Han C Z，et al.A novel approximation of basic probability assignment based on rank-level fusion［J］.Chinese Journal Aeronautics，2013，26（4）：993－999.

［9］Dezert J，Han D Q，Liu Z G，et al.Hierarchical proportional redistribution principle for uncertainty reduction and BBA approximation［J］.Belief Functions：Theory and Applications，2012：275－283.

［10］Li X D，Dezert J，Smarandache F，et al.Evidence supporting measure of similarity for reducing the complexity in information fusion［J］.Information Sciences，2011，181（10）：1818－1835.

［11］Liu Z G，Pan Q，Dezert J.A new belief-based K-nearest neighbor classification method［J］.Pattern Recognition，2013，46（3）：834－844.

［12］Yang Y，Han D Q，Han C Z.Discounted combination of unreliable evidence using degree of disagreement［J］.International Journal of Approximate Reasoning，2013，54：1197－1216.

［13］Peng Y，Hu Z H，Shen H R.A modified distance of evidence［J］.Journal of Electronics ＆Information Technology，2013，35（7）：1624－1629.（彭颖，胡增辉，沈怀荣.一种修正证据距离［J］.电子与信息学报，2013，35（7）：1624－1629.）

［14］Gordon J，Edward H，Shortliffe.A method for managing evidential reasoning in a hierarchical hypothesis space［J］.Artificial Intelligence，1985，26（3）：323－357.

［15］Li X D，Dezert J，Huang X H，et.al.A fast approximate reasoning method in hierarchical DSmT（A）［J］.Acta Electronica Sinica，2010，38（11）：2566－2572.（李新德，Dezert J，黄心汉，等.一种快速分层递阶DSmT近似推理融合方法（A）［J］.电子学报，2010，38（11）：2566－2572.）

［16］Li X D，Wu X J，Sun J M，et al.An approximate reasoning method in Dezert-Smarandache Theory［J］.Journal of Electronics，2009，26（6）：738－745.

［17］Li X D，Yang W D，Wu X J，et al.A fast approximate reasoning method in hierarchical DSmT（B）［J］.Acta Electronica Sinica，2011，39（A03）：31－36.（李新德，杨伟东，吴雪建，等.一种快速分层递阶DSmT近似推理融合方法（B）［J］.电子学报，2011，39（A03）：31－36.）

［18］Li X D，Yang W D，Dezert J，et al.A fast approximate reasoning method in hierarchical DSmT（C）［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2011，39（S2）：150－156.（李新德，杨伟东，Dezert J，等.一种快速分层递阶DSmT近似推理融合方法（C）［J］.华中科技大学学报（自然科学版），2011，39（S2）：150－156.）

［19］Dezert J，Smarandache F.Partial ordering on hyper-power sets［A］∥Dezert J，Smarandache F.Advances and applications of DSmT for information fusion（Collected Works Vol.I）.Rehoboth：American Research Press，2004.

［20］Martin A.Implementing general belief function framework with a practical codification for low complexity［A］∥Dezert J， Smarandache F.Advances and applications of DSmT for information fusion（Collected Works Vol.III）.Rehoboth：American Research Press，2009.

Modified evidence coding method based on Dezert-Smarandache theory

LI Hong-fei1，JIN Hong-bin1，TIAN Kang-sheng1，WANG Jing2
（1.The 4th Department，Air Force Early Warning Academy，Wuhan 430019，China；2.Beijing Yunxingyu Technology Service Co.，Ltd，Beijing 100078，China）

The calculation is one of the important issues which affect the application of the Dezert-Smarandache theory（DSmT）.The research of the calculation is a hotspot in the area of the DSmT.The calculation code is widely recognized for the reasonability of evidence expression and belief computation.The calculation code is simple and effective in the coding process.But all possible elements should be searched in the decoding process which causes large calculation amount to reduce the efficiency of calculation code.To solve the problem，a modified evidence coding method is presented.In the modified method，the exclusive position attribution based on the focal element relationship is added to reduce the large calculation amount in the decoding process.The exclusive position attribution is generated and stored in the database before evidence processing.The simulation example verifies the validity of the combination result and the high efficiency in the calculation.

Dezert-Smarandache theory（DSmT）；evidence code；calculation analysis；calculation code；decoding transform

TP 14

10.3969／j.issn.1001-506X.2015.08.31

李鸿飞（1984－），男，博士研究生，主要研究方向为不确定性推理理论及其军事应用。

E-mail：kjld＿lhf＠163.com

金宏斌（1976－），男，副教授，博士，主要研究方向为数据融合、目标识别。

E-mail：jhbo817＠tom.com

田康生（1964－），男，教授，博士研究生导师，主要研究方向为军事信息系统、效能评估。

E-mail：tiankangsheng＠tom.com

王晶（1981－），女，工程师，硕士，主要研究方向为计算机应用。

E-mail：wabmwj007＠163.com

1001－506X201508－1922－06