非连续性的复合量化句逻辑语法处理方式*

邹崇理

(中国社会科学院哲学所,北京100732)

非连续性的复合量化句逻辑语法处理方式*

邹崇理

(中国社会科学院哲学所,北京100732)

【主持人语】 本期刊登两篇有关研究逻辑语法的文章。

信息时代的核心技术之一是自然语言信息处理,而自然语言信息处理的前提是把自然语言句法语义形式化。以下两篇文章都是对自然语言形式化研究的成果,这有助于计算机的自然语言信息处理。早在卡尔纳普和莫里斯那里,自然语言就分为句法、语义和语用三个层面。从句法角度看,自然语言表达式总是前后相连的符号串,但从语义视角看,这些符号串的语义运算并非都是相邻毗连的。句法相邻而语义分离的错位现象常常可以见到,这就是自然语言中的非连续结构,而复合量化句呈现出独特的非连续性特点。邹崇理研究员在此先后介绍范畴语法和蒙太格语法对非连续结构的处理方式,对此做出一些扩展来处理非连续的复合量化句,最后评价两种方法的优劣和提出探索的问题。

姚从军副教授关注的范畴语法是一种用于计算的关于自然语言的语法。范畴语法的两个最完善的分支是基于逻辑传统的范畴类型逻辑和基于组合传统的组合范畴语法,二者联系紧密,差异也明显,前者主要关心不同逻辑算子对语言的适用性和逻辑系统的证明论性质,理论价值大于计算应用的价值。后者具有良好的计算性质,在信息处理领域影响很大。二者具有互补作用。

从纯句法角度看,自然语言表达式表现为由小到大生成的连续符号串。大多数情况下,这些符号串的语义追随句法进行毗连组合。但在不少场合下,这种句法和语义的对应出现错位,句法的生成和语义的组合对应不起来,即句法上分离的符号串在语义上是不可分离的整体。这就是自然语言中的非连续结构,而复合量化句呈现出独特的非连续性特点。本文先后介绍范畴语法和蒙太格语法对非连续结构的处理方式,对此做出一些扩展,最后评价两种方法的优劣和需要探索的问题。

非连续结构;复合量化句;范畴语法;蒙太格语法

信息时代的核心技术是计算机信息处理,特别是关于自然语言的信息处理。自然语言信息处理的前提是对句法语义丰富多样的自然语言进行形式化分析,20世纪60年代诞生的逻辑语法(又叫形式语义学)系列学科为此应运而生,其中的范畴语法和蒙太格语法影响最大,其处理自然语言的最大难点就是自然语言中的非连续结构(discontinuous structure)。

什么是自然语言中的“非连续结构”。组合范畴语法的创立者Steedman认为:“自然语言中的非连续结构是范畴语法以及其他语法理论的核心问题(Steedman 1987)。”通常把关系从句、疑问句、话题句、断裂句和准断裂句等无界限依存结构认为是非连续结构。古典范畴语法只能把相邻(adjacent)两成分毗连(concatenation)在一起,语义上其中一个是函数表达式,另一个是论元表达式,二者之间进行函数运算。Wood提出如果可作函数运算的两成分句法上不相邻,则无法直接毗连,这就是不连续现象(Wood 1993)。Morrill提出动词省略和照应回指现象等属于非连续结构(Morrill 2011),把非连续结构定义为句法和语义的不匹配(the mismatch between syntax and semantics)(Morrill 1995;Morrill 2011),本文讨论的非连续的量化复合句就属于这样的情况。

先看看英语的一些非连续结构,如:

(1)Mary let John down

Let…down的意思是“令人失望”,就是说let…down在语义上是一个不可再分的基本单位,可是在句法上却由不相邻的两个单词构成。虽然let…down可以针对John做语义运算,但句法上却需要把后者插入到前者两个单词之间。英语中还有一些习语,如:

(2)Mary gave John the cold shoulder

从语义角度看,“give…the cold shoulder”可以对应一个语义算子,而“John”对应这个算子的论元。但是在句法上,语义算子和语义论元对应的表达式却是分开的,这就是句法和语义不匹配造成的非连续结构。

范畴语法怎样处理自然语言的非连续结构?古典范畴语法限于处理相邻的两个句法表达式,只有毗连(concatenation)一种句法操作,所谓毗连是指给定任意两个语符串α和β,把它们毗连在一起得到α β或者βα。范畴语法中强调函数运算的表述就是:若α的范畴是A/B,β的范畴是B,则αβ的范畴是A。现代范畴语法用包裹(wrapping)这种句法操作(syntactic operation)来处理不连续现象。给定任意两个表达式,依照某一句法规则,经某种句法操作,二者可生成一个句法整体。为了生成如“gave John the cold shoulder”一类的表达式,Bach在范畴语法中引进了右包裹操作(Bach 1989):

若a形如[XPXW],则RWAP(a,b)=X_b_W。

应用于(2)就得:

RWRAP((gave the cold shoulder),John)=gave John the cold shoulder

为解决自然语言在句法和语义上不匹配的非连续结构,Morrill提出了不连续兰贝克演算DLC (Discontinuous Lambek Calculus)。基于DLC的范畴语法,其词库里的词条内容是句法形式、所属范畴和语义表达式的三元组,某些词条的句法形式增加了表示不连续的结构成分,即语言成分之间的间隙(gap),比如:

give…the cold shoulder⇒give+1+the+cold+shoulder:(nps)↑np:shun

也就是把非连续的句法表达式“give…the cold shoulder”改写成含有毗连算子“+”和间隙“1”的句法形式“give+1+the+cold+shoulder”,用包含上箭头算子的范畴“(nps)↑np”作为该句法形式的范畴,用shun作为这个句法形式的语义表达式。DLC处理英语中一个不连续语句的范畴语法推演如下:

什么是非连续的复合量化句?量化句指的是包含量词的句子,量词在自然语言中表现为“每个”“一个”“不同一本”之类的限定词(determiner),复合的量化句就是包含两个以上量词的句子。我们来看通常的汉语复合量化句:

(4)每个选民都选举一个候选者。

这里“每个”和“一个”就是(4)包含的两个量词,通常一阶逻辑和广义量词理论对(4)的语义表述是:①以下借用汉语词的黑体来表示其对应的谓词常项。

一阶逻辑方式:∀x[选民(x)→∃y[候选者(y)&选举(x,y)]

广义量词方式:EVERY(选民,λx(SOME(候选者)(λy(选举(x,y)))))

虽然上述语义表述存在不够精细之处,②就某个选民而言,他选举的候选者跟其他选民选择的候选者是相同还是不同,语句(3)本身没有进一步说明,一阶逻辑的方式和通常广义量词理论的方式对此也不能进行更精细的分析。但从广义量词角度看量词“EVERY”和“SOME”的涵义是各自独立的,(3)不属于非连续的复合量化句。下述复合量化句的情况就不同了:

(5)每个学生(都)读不同一本书。

显然,一阶逻辑和通常广义量词的表述方式不便分析(5)的语义特征。(5)说的是“学生”集合中的成员通过“读”对应的“书”集合中的成员是各不相同的,这种对应是一一对应,学生甲读的书不同于学生乙读的书,两个不同学生不能读同一本书。按照Keenan的方法(Keenan 1986),我们用集合A代表“学生”,用集合B代表“书”,“每个……不同一本…”这个复合量词用Q[每个…]表示,A和B可以作为这个复合量词的两个论元。二元关系R 表示“读”,是这个量词的第三个论元。而Ra表示由个体a作为R的前项所决定的R的后项的集合,(5)的量化表述为:

Q[每个……不同一本…](A,B,R)

(6)的语义解释为:

(7)Q[每个……不同一本…](A,B,R)=1当且仅当

1.∀a,b∈A且a≠b:RaB≠RbB

2.∀a∈A:|RaB|=1

(7)用两条陈述表明量化公式(6)的语义。第1陈述说的是,对于任两个不同的学生a和b来说,a读的书的集合RaB不同于b读的书的集合RbB;第2陈述意味,任何一个学生a读的书的集合中只有一个成员,即一本书。这里我们强调的是,(5)中的两个量词“每个”和“不同一本”的量化涵义不是独自分离的,它们必须结合在一起才能确立(7)所显示的两条陈述,(7)中的Q[每个…同样一本…]其量化语义是一个整体。而(5)中体现量化语义的句法成分“每个”与“不同一本”却不是毗连相邻的,句法和语义在这里不匹配,这就是复合量化句中的非连续结构,或者叫非连续的复合量化句。

按照范畴语法的方式,即Morrill提出的不连续兰贝克演算DLC,是否能够处理上述非连续的复合量化句?我们列举Morrill的DLC中处理不连续结构的两个推演规则:③这里Morrill用“,”替代“…”表示间隙。为直观简明起见,我们从Jäger(Jäger 2005)中转引Morrill在2000年的表述,而不用Morrill在2011年著述中的更具一般性的表述。

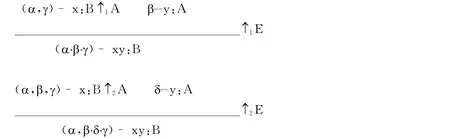
规则↑1E生成具有一个间隙的非连续结构,如同(3)中的推演。而规则↑2E用于生成具有两个间隙的不连续结构。由于(6)分析出的复合量词严格讲具有三个间隙,第一个间隙插入“学生”,第二个间隙插入“读”,第三个间隙插入“书”。关键是,前两个间隙是相毗连的,第三个间隙后面没有符号串。这些情况是Morrill的规则所没有描述的,由此可见,范畴语法处理非连续结构的规则对非连续的量化复合句来说似乎需要进一步扩展。

怎样扩展?笔者先定义具有连续间隙的符号串和具有右空符号串的间隙,在Morrill的有关定义那里,增加一条补充:

3′ 若α,β∈T1,则(α,,β,)∈T2

再增加相应的推演规则:

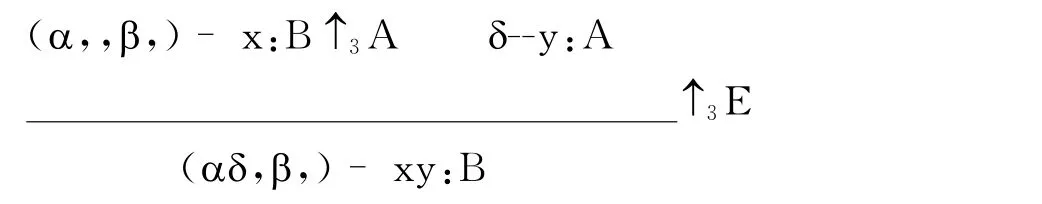
于是(6)的生成过程表现为依次应用↑3E、↑2E和↑1E的推演:

然而,蒙太格对非连续复合量化句的处理似乎更加精巧便利,蒙太格式的构建语句系统的方式对此大有用武之地。Keenan对非连续复合量化句的分析非常到位,颇具影响力。然而在Keenan那里,没有系统的生成复合量化句的规则,仅仅给出复合量词整体的语义解释,没有给出复合量化句的生成过程。这使我们回想到蒙太格语法(Montague Grammar)当初处理量化句的独特方式,即不单列出量词范畴的做法(Montague 1974),有其独特的精妙之处。把这种方式进一步扩展,对复合量化句的生成是很方便的。我们先来看Montague的PTQ系统对量化表达式的生成规则:

S2.若ζ∈PCN,则F0(ζ),F1(ζ),F2(ζ)∈PT,其中:

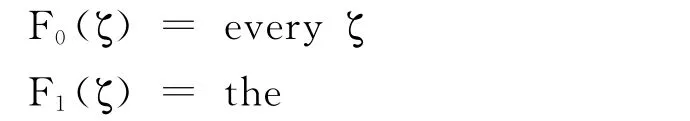
F2(ζ)=aζ或anζ,依据ζ词头第一个字母是辅音读法还是元音读法。

对应的翻译规则为:

TR2.若α∈PCN,α翻译成α′,则F0(α)=everyα译为:λQ∀z[α′(z)→Q(z)]

F1(α)=theα译作:λQ∃x[∀y[α′(y)↔y=x]∧Q(x)]

F2(α)=aα译为:λQ∃z[α′(z)∧Q(z)]

这里,Montague生成量化短语的方式非常独特,在句法规则中不把量词当作独立的句法范畴。仅仅通过句法操作F把量词插入到通名前而形成量词短语。而对应这样的句法操作F的表现语义的翻译操作也很巧妙,其灵活性使得蒙太格式的语句系统生成非连续的复合量化句显得非常方便。如生成(5)的句法规则就是:

Syn1.若α,β∈PCN,γ∈PVT,则F1(α,β,γ)=每个αγ不同一本β∈Pt。

相应的翻译规则为:

Tr1.若α′,β′是α,β的翻译,γ′是γ的翻译,则F1(α,β,γ)翻译为:Q[每个…不同一本…](α′,β′,γ′)。

而非连续的复合量词的语义解释(7)为:①Keenan对复合量词的解释体现出一种函项映射的思想。我们设置一个函项f,限制为一一函项,就能准确揭示(6)的量化语义,对Keenan的语义解释的改进是:Q[每个…不同的一本…](A,B,R)⇔存在一一映射的函项f:A⇨B, f即是R。即∀a,b∈A且a≠b:f(a)≠f(b)。关于复合量词语义解释的改进这里从略。

Q[每个……不同一本…](α′,β′,γ′)当且仅当 存在一一映射的函项f:α′⇨β′,f就是γ′。

自然语言中还有大量的非连续复合量化句,以汉语为例:②关于汉语非连续的复合量化句的详细论述参见(张世宁2006)。

(8)每个学生(都)读了同样一本书

(9)每个学生(都)读了同样三本书

(10)每个学生(都)读了同样一些书

(11)至少两个学生问了那个老师同样一个问题。

用蒙太格语法构造语句系统的方式,可以确立生成上述非连续复合量化句的句法规则:

Syn2.如果α,β∈PCN,γ∈PVT,则F2(α,β,γ)=每个αγ同样一本β∈Pt。

Syn3.如果α,β∈PCN,γ∈PVT,则F3(α,β,γ)=每个αγ同样三本β∈Pt。

Syn4.如果α,β∈PCN,γ∈PVT,则F4(α,β,γ)=每个αγ同样一些β∈Pt。

Syn5.如果α,β,δ∈PCN,γ∈PVT3,则F5(α,β,δ,γ)=至少两个αγ那个β同样一个δ∈Pt。

对应的翻译规则可以像范畴语法那样给出自然语言表达式的逻辑式:

Tr2.如果α′,β′分别是α,β的翻译,γ′是γ的翻译,则F2(α,β,γ)的翻译是:

Q[每个……同样一本…](α′,β′,γ′)。

Tr3.如果α′,β′分别是α,β的翻译,γ′是γ的翻译,则F3(α,β,γ)的翻译是:

Q[每个……同样三本…](α′,β′,γ′)。

Tr4.如果α′,β′分别是α,β的翻译,γ′是γ的翻译,则F4(α,β,γ)的翻译是:

Q[每个……同样一些…](α′,β′,γ′)。

Tr5.如果α′,β′,δ′分别是α,β,δ的翻译,γ′是γ的翻译,则F5(α,β,δ,γ)的翻译是:

Q[至少两个……那个…同样一个…](α′,β′,γ′,δ′)。

结束语:以上我们简略地介绍了非连续的复合量化句的情况。自然语言中存在大量的非连续现象,复合量化句能够显示出这样的非连续性——句法和语义的不匹配,即通过句法分离的方式表现出一个完整的语义。其次,我们分别给出范畴语法和蒙太格语法处理自然语言非连续现象的不同方式,前者采用类似引入或消去逻辑连接词的推演规则来展示非连续的复合量化句的句法和语义的生成过程,后者采取构造自然语言语句系统的规则方式说明这样的过程。③本文对Morrill的非连续兰贝克演算的规则做了扩充,同时对刻画复合量化句的蒙太格语句系统的规则也做了增添。现在我们就来比较比较两种方法的利弊优劣。

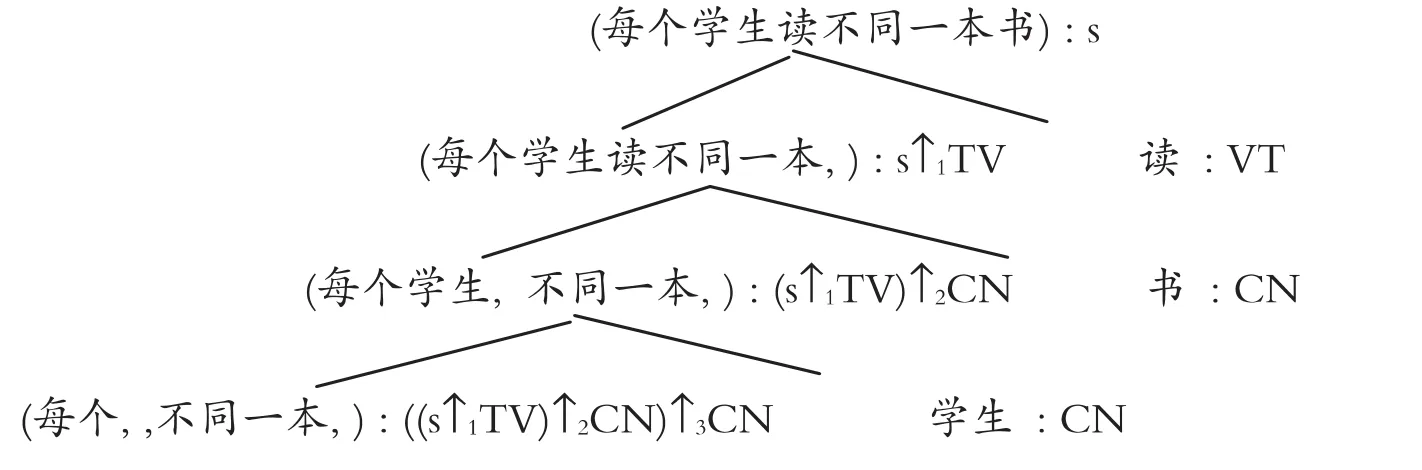
范畴语法处理非连续结构的方式具有逻辑学追求的简洁精准性,每一步推演根据一个规则,一个规则执行一个操作。推演树(7′)可以重新表述为:④为了最直接展示语言的生成过程,我们在此略去了每个节点对应的逻辑式。这是一种两分法的分析,从逻辑角度看没有什么不妥。但是从语言直觉感受来讲,非连续的复合量词的符号串本身就不自然,除最后一步的每一步插入一个词所得结果也不符合人们构词造句的语言习惯。

对此蒙太格语法的分析树是:

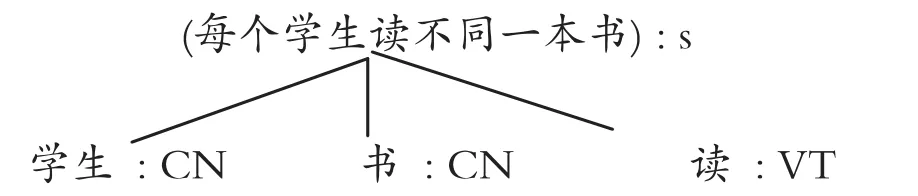
这是多分法的结果,步骤简单,每个节点对应的自然语言符号串都是人们语言习惯所能接受的,因此从语言直觉看,蒙太格语法生成非连续复合量化句的方式显得自然简便。从计算语言学角度看,蒙太格语法的多分法操作比范畴语法的两分法操作效率高。

最后,我们需要进一步探讨的问题是,按照范畴语法的词汇主义思想,包含三个间隙的非连续结构“每个,,不同一本,”并非最小的词条单位,怎样理解它的生成过程?①蒙太格语法不把量词作为一个独立的句法单位,回避了复合量词的生成过程的理解问题。按照广义量词理论,复合量词总是由简单量词根据严格的叠置定义叠置复合而成。但是非连续的复合量词显示出特殊性,即复合前的单个量词成分如“不同一本”还不好算作是具有独立涵义的简单量词,这样能够适用于广义量词理论中严格的量词复合的叠置定义吗?如果能够纳入到量词复合的叠置定义中被说明,复合前的量词成分如“不同一本”的量化涵义怎样确立?非连续复合量词的生成在范畴语法中似乎应该确立特定的推演规则。

Linguistic logic in discontinuously compound quantified sentences

ZOU Chong-li
(Institute of Philosophy,Chinese Academy of Social Sciences,Beijing 100732,China)

From a purely syntactic perspective,natural language expressions are characterized by continuous symbolic strings generated from small parts to large ones.Mostly,by following their syntax,the semantic meanings of these symbolic strings are also concatenate.But in many cases,the correspondences between their syntax and semantics are dislocated,which means that their syntactic generation and semantic composition cannot match with each other;for instances,syntactically separated symbolic strings are inseparable as a whole semantically.This is the discontinuous structure of natural language.Compound quantified sentences present the unique characteristics of discontinuity. This paper briefs the approaches to the discontinuous structure in the framework of categorical grammar and Montague grammar and somewhat improves their methods.Finally,the paper evaluates the merits and weaknesses of the two methods and proposes the future research questions.

discontinuous structure;compound quantified sentences;categorical grammar,Montague grammar

B81-092

A

1000-5110(2015)01-0069-06

[责任编辑: 王德明]

邹崇理,男,四川成都人,中国社会科学院创新工程首席研究员,博士生导师,中国逻辑学会会长,国家重大课题首席专家,研究方向为语言逻辑。

国家社科基金重大课题“自然语言信息处理的逻辑语义学研究”(10&ZD073)。