联箱匹配对U型布置并联管组换热器流量分配影响研究

曲新鹤，孙中宁，丁 铭

（1.清华大学 核能与新能源技术研究院，北京 100084；2.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001）

联箱匹配对U型布置并联管组换热器流量分配影响研究

曲新鹤1，孙中宁2，丁 铭2

（1.清华大学 核能与新能源技术研究院，北京 100084；2.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001）

借助ANSYS FLUENT软件，使用Realizable k-ε湍流模型对U型布置的动量恢复型并联管组模型进行数值计算，并从联箱内压力变化的角度分析推导得出最佳联箱截面比（OARH）的计算公式。结果表明，分配联箱和汇流联箱截面比对并联管组流量分配有很大影响，使用数值计算和分析方法得出的OARH均在0.6左右。本文提出的联箱尺寸匹配方法可增强并联管组换热器流量分配均匀性，并为换热器的联箱设计提供理论指导。

最佳联箱截面比；并联管组；U型布置；动量恢复；流量分配；Realizable k-ε模型

新一代反应堆采用非能动安全壳导热系统（PCCS）在严重事故时排出安全壳内的热量，系统内部换热器常采用并联管组换热器形式，它的流量分配对于系统的安全稳定运行至关重要。并联管组换热器在其他一些领域也有广泛应用，且研究较早，如电站锅炉系统中的过热器和省煤器、太阳能集热系统、燃料电池、电子冷却装置等。研究表明，换热器分配联箱和汇流联箱内的压力分布是影响换热器流量分配的决定性因素，而联箱内的压力变化是摩擦阻力和动量恢复共同作用的结果。Acrivos等［1］提出，流动不均匀性是由于联箱内的压力变化导致的，大的分配联箱和汇流联箱截面会增强流动的均匀性。赵镇南［2］建立了U型布置时联箱内速度分布的一维无量纲微分方程，在忽略联箱摩擦压降的条件下，得到联箱压力分布、各支管流量分配及整个换热器总压降的解析式。Wang［3］同样建立了U型布置时联箱速度分布的一维无量纲微分方程，在考虑了联箱内的摩擦阻力和动量恢复的情况下得到了联箱内压力分布的分析解，虽然其表达式中含有分配联箱和汇流联箱截面比，但未对这一比值对流量分配的影响进行分析和讨论。

这些研究初步揭示了分配联箱和汇流联箱的截面比（ARH）对换热器流量分配的影响，但尚未对其进行更加深入的讨论。本文从数值模拟和分析方法两个方面对这一问题进行分析研究。

1 数值计算

1.1 几何模型与数值计算设置

为研究ARH对并联管组换热器流量分配的影响，先对U型布置并联管组换热器模型进行数值模拟。ARH的定义式如式（1）所示。几何模型（图1）分为3组，其中相同的尺寸为：分配联箱和汇流联箱中心线间距离2 000mm，换热管直径32mm，换热管截距64mm，联箱长度2 134mm。不同的尺寸为：3组模型的汇流联箱直径Dh分别为80、100和120mm，对于每一组模型，改变其分配联箱直径Df，使得ARH从0.2变化到1.6。

其中：Af为分配联箱截面积，m2；Ah为汇流联箱截面积，m2。

图1 并联管组换热器几何模型Fig.1 Geometry model of parallel manifold of heat exchanger

数值计算的前处理采用Gambit软件进行网格划分，网格均为六面体结构化网格，所有算例中网格最大倾斜度均不高于0.6。经网格无关性验证，对于不同几何模型，网格数在200万～350万范围内。流动介质为单相水，等温流动，雷诺数在104～105范围内。选择稳态压力基求解器，速度压力耦合处理采用SIMPLE算法。湍流模型选择Realizable k-ε模型［4］，壁面处理采用Scalable壁面函数。压力的空间离散采用PRESTO！格式，动量方程、湍流动能方程、湍流耗散方程的离散采用高阶QUICK格式。边界条件为速度入口和压力出口，入口使用profile文件编写充分发展入口条件，以避免入口效应对计算结果的影响。

1.2 联箱截面比对流量分配的影响

定义两个衡量并联管组换热器流量分配均匀性的因子Ei和SEi用以衡量换热器整体的流量分配均匀性。其中：Ei为各根换热管流量相对于平均流量的偏差；对所有换热管的Ei进行绝对值求和即得到SEi，SEi越小说明系统流量分配越均匀。Ei和SEi的定义式如下：

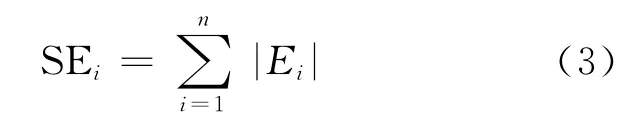
其中：vi为第i根管的流速，m／s；vav为各根管的平均流速，m／s。

分别对3组换热器模型在入口体积流量Q为5m3／h时进行数值模拟。图2示出ARH对并联管组换热器流量分配的影响。图2a的汇流联箱直径为100mm。从图2a可看出：在ARH较小时，靠近分配联箱末端的换热管流量高于平均值，靠近分配联箱入口端的换热管流量低于平均值；ARH越小，不均匀现象越明显；在ARH较大时，流量分配规律则相反，靠近入口端的换热管流量高于平均值，ARH越大，不均匀分配情况越明显。当ARH等于0.61时，各根换热管的流量相对均匀。

图2 联箱截面比对并联管组换热器流量分配的影响Fig.2 Effect of cross section area ratio of header on flow distribution of parallel manifold of heat exchanger

从图2b可看出，在汇流联箱直径不变、增大分配联箱直径的过程中，SEi并非单调的，而是存在一最小值，即存在一最佳的流量分配效果。将SEi最小时的ARH定义为最佳联箱截面比（OARH）。对比ARH小于OARH时和大于OARH两种情况，前者ARH对于流量分配的影响更为剧烈，后者相对平缓。对于相同的ARH，Dh越大，SEi越小，说明增大联箱直径有助于增强系统流量分配的均匀性。表1列出3个换热器模型的流量分配情况。从表1可看出，整体增大两个联箱的直径或对两个联箱进行适当匹配，均可达到增强系统流量分配均匀性的目的，且后者具有更好的效果，特别在联箱直径受到限制时，后者更具有优势。

表1 不同并联管组模型流量分配均匀性比较Table 1 Comparison of flow distribution uniformity at different parallel manifold models

另外，对汇流联箱直径为100mm的一组换热器模型在入口体积流量分别为5、10、15和50m3／h的情况进行模拟，结果示于图3。从图3可看出：在ARH＜OARH时，入口流量对换热器流量分配影响较大，随入口流量增大，流量分配的不均匀性增强；在ARH＞OARH时，入口流量对换热器流量分配影响很小。另外，随入口流量增大，OARH略有增大，从0.608增大到0.648。

图3 入口流量对并联管组换热器流量分配的影响Fig.3 Effect of inlet flow rate on flow distribution of parallel manifold of heat exchanger

2 理论分析

2.1 联箱压力变化与换热器流量分配的关系

已有的对并联管组流量分配的研究表明换热管中的流量由其进出口的压差决定，也即由分配联箱和汇流联箱内的压力分布控制。联箱内的压力变化是动量恢复和摩擦阻力共同作用的结果。分配联箱内动量恢复大于摩擦阻力引起的压力变化的换热器称为动量恢复型并联管组换热器，摩擦阻力大于动量恢复引起的压力变化的换热器称为摩阻控制型并联管组换热器［56］。目前使用的联箱通常尺寸较短，且联箱直径较大，因此摩擦阻力对压力变化的影响较小，大多为动量恢复型。前面的数值计算及以下分析均针对U型布置的动量恢复型并联管组换热器。

图4示出并联管组换热器内部压力标记图。如图4所示，要保证并联管组换热器各根换热管的流量均匀分配，则各根换热管入口和出口间的压差Δpt，i必须相等，即：

图4 并联管组换热器内部压力标记图Fig.4 Mark figure of pressure in parallel manifold of heat exchanger

令：

则有：

将式（7）带入式（5）可得到：

由上面的推导可知，换热器流量均匀分配的条件等价于分配联箱和汇流联箱内压力沿联箱轴向变化相同。对于U型布置动量恢复型的并联管组换热器，联箱内压力沿联箱轴向变化是单调的，故可简化为式（8）中的最后一项（Δpf，n＝Δph，n），作为流量均匀分配的条件。图5示出联箱内压力的变化。对应于图4，Δpf，n即为Δpf，Δph，n即为Δph，则式（8）简化为式（9）：

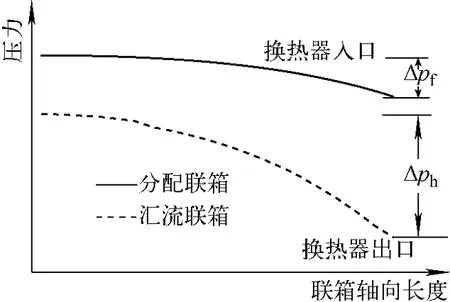
图5 联箱内压力的变化Fig.5 Pressure change in header

利用静压转换系数可将联箱内的压力变化与联箱内的流量联系起来，假设pf，L＝pf，n、ph，L＝ph，n，则有：

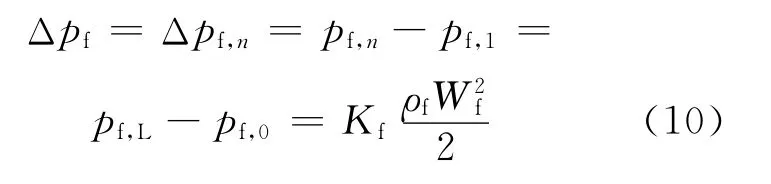
式中：Kf、Kh分别为分配联箱和汇流联箱静压转换系数；Wf、Wh分别为分配联箱和汇流联箱入口流速，m／s；ρf、ρh分别为分配联箱和汇流联箱内介质密度，m3／kg；pf，L、ph，L分别为分配联箱和汇流联箱末端压力（如图4所示），Pa。

文献［7］给出的Kf和Kh的表达式为：

式中：cf和ch分别为静压分布参数，由实验测定；L为联箱长度，m；D为联箱直径，m；λ为联箱内沿程摩擦阻力系数。

2.2 OARH计算式推导

由上述分析得知，式（9）为换热器流量均匀分配的条件，将式（10）、（11）代入式（9）可得到：

化简得到：

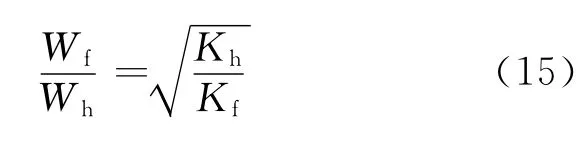
连续性条件为换热器进出口质量流量相等，即：

联立式（15）、（16）可得到：

把式（12）、（13）代入式（17），得到OARH的计算式：

式（18）中有两点需要注意：1）式中含有摩擦阻力项，需已知分配联箱和汇流联箱长径比（L／D），故需要简单的迭代计算；2）式中的摩擦阻力系数λ按照光滑管使用勃拉休斯或尼古拉斯计算式计算。

3 结果比较

式（18）在使用上有一主要的限制因素，即cf和ch的确定，虽有一些实验结果，但差别较大［89］。表2为使用文献［8-9］的实验结果代入式（18）得到的OARH与数值计算得到的OARH的比较，其中，换热器入口体积流量均为5m3／h。由表2可看出，使用式（18）得到的OARH与数值计算结果符合得相对较好，式（18）的计算结果基本要较数值计算结果小，且相对偏差均随联箱直径增大而增大。

分析造成以上偏差的原因，由于数值计算是将多个算例结果进行比较分析，得到具有最好的流量分配效果的几何模型，但严格意义上说并不是绝对的均匀分配，而式（18）是在换热器流量绝对均匀分配的情况下得出的。存在偏差的另一原因主要是cf和ch的选择。从结果比较中可看出，偏差有的很小，有的则相对较大，这说明将cf和ch取为定值是不合理的，cf和ch应受到联箱内分流比、联箱和换热管截面比等因素的影响，选择更合适的cf和ch会增强公式的准确性。

表2 OARH的数值计算与式（18）计算结果比较Table 2 Comparison of OARH by both numerical simulation and Eq.（18）

4 结论

并联管组换热器的流量分配对于其流动损失和换热功率等性能参数均有影响。本文针对使用较为广泛的U型布置的动量恢复型并联管组换热器，提出了一种通过调节分配联箱和汇流联箱截面比来增强换热器流量分配均匀性的方法。通过数值计算方法发现联箱截面比对换热器流量分配有较大影响，从联箱内压力变化的角度推导出OARH的计算公式。数值计算结果与使用式（18）计算得到的结果吻合得较好，OARH均在0.6左右。本文提出的方法可为并联管组换热器的设计提供指导。

［1］ ACRIVOS A，BABCOCK B D，PIGFORD R L.Flow distributions in manifolds［J］.Chemical Engineering Science，1959，10：112-124.

［2］ 赵镇南.集管系统压力与流量分布的研究，1：U型布置时的分析解［J］.太阳能学报，1999，20（4）：377-384.

ZHAO Zhennan.An investigation on pressure and flow distribution in manifolds，1：Analytical solution for U-type arrangement［J］.Acta Energiae Solaris Sinica，1999，20（4）：377-384（in Chinese）.

［3］ WANG Junye.Pressure drop and flow distribu-tion in parallel-channel configurations of fuel cells：U-type arrangement［J］.International Journal of Hydrogen Energy，2008，33：6 339-6 350.

［4］ CHEN A，SPARROW E M.Turbulence modeling for flow in a distribution manifold［J］.International Journal of Heat and Mass Transfer，2009，52：1 573-1 581.

［5］ 王恩禄，田子平，缪正清.分配联箱静压分布参数Cf值的理论分析［J］.动力工程，1997，17（3）：26-31.

WANG Enlu，TIAN Ziping，MIAO Zhengqing.The theoretical analyses on hydrostatic pressure distribution parameter Cfof distributing headers［J］.Power Engineering，1997，17（3）：26-31（in Chinese）.

［6］ 王恩禄，田子平，缪正清，等.分配联箱静压分布参数Ch值的理论分析［J］.动力工程，1997，17（6）：73-78.

WANG Enlu，TIAN Ziping，MIAO Zhengqing，et al.The theoretical analyses on hydrostatic pressure distribution parameter Chof collecting headers［J］.Power Engineering，1997，17（6）：73-78（in Chinese）.

［7］ 哈尔滨锅炉厂.电站锅炉水动力计算方法［S］.上海：上海发电设备成套设计研究所，1983.

［8］ 陈之航，赵再三.单相流体在并联管组中的流量分布和热偏差的理论及计算［J］.锅炉技术，1974，5（10）：294-314.

CHEN Zhihang，ZHAO Zaisan.Theory and calculation of the flow distribution and thermal deviation of the single fluid in parallel tubes［J］.Boiler Technology，1974，5（10）：294-314（in Chinese）.

［9］ BAJURA R A.A model for flow distribution in manifolds［J］.Journal of Fluid Engineering，1971，1：7-12.

Study on Effect of Header Match on Flow Distribution in U-type Arrangement Parallel Manifold of Heat Exchanger

QU Xin-he1，SUN Zhong-ning2，DING Ming2
（1.Institute of Nuclear and New Energy Technology，Tsinghua University，Beijing100084，China；2.Fundamental Science on Nuclear Safety and Simulation Technology Laboratory，Harbin Engineering University，Harbin150001，China）

The numerical simulation to U-type momentum regaining parallel manifold was completed with Realizable k-εmodel by means of the ANSYS FLUENT software.An analytic method for the optimal cross section area ratio of the header（OARH）was obtained on the basis of the pressure change within the headers.The results show that the cross section area ratio of the dividing header to the combining header has a large effect on the flow distribution in the manifold，and the OARH obtained by both numerical simulation and analytic method is about 0.6.The method to match header can enhance the flow distribution uniformity in the parallel manifold of heat exchanger，and offer a guide for the design of the manifold of heat exchanger.

optimal cross section area ratio of header；parallel manifold；U-type arrangement；momentum regaining；flow distribution；Realizable k-εmodel

TK172

：A

1000-6931（2015）04-0623-06

10.7538／yzk.2015.49.04.0623

2013-12-30；

2014-10-08

曲新鹤（1988—），女，黑龙江鹤岗人，博士研究生，核能科学与工程专业