内圈故障滚动轴承系统周期运动的倍化分岔

王强，刘永葆，2，徐慧东，贺星，刘树勇

(1.海军工程大学动力工程学院，武汉430030;2.舰船动力军队重点实验室，武汉430030; 3.太原理工大学力学学院，太原030024)

内圈故障滚动轴承系统周期运动的倍化分岔

王强1，刘永葆1，2，徐慧东3，贺星1，刘树勇1

(1.海军工程大学动力工程学院，武汉430030;2.舰船动力军队重点实验室，武汉430030; 3.太原理工大学力学学院，太原030024)

针对轴承内圈破损故障，建立轴承三自由度分段非光滑的故障模型，研究内圈故障滚动轴承系统周期运动的倍化分岔现象和混沌行为;求出系统的切换矩阵后，将得到的切换矩阵结合光滑系统的Floquet理论来分析轴承非光滑系统周期运动发生倍化分岔的条件。通过在碰撞面处建立Poincaré映射，用数值方法进一步揭示轴承系统的周期运动经倍化分岔通向混沌的现象;结果表明，当旋转频率接近临界分岔点时，系统有1个Floquet特征乘子接近－1，系统发生周期倍化分岔，随着旋转频率的增加，系统经历了周期二解的Nermark－Sacker分岔，随后又经历了多周期、混沌等复杂的非线性行为。对该故障轴承系统分岔和混沌的研究，可为大型高速旋转机械的安全稳定运行提供可靠的设计与故障诊断依据，也为实际设计时提供理论指导和技术支持。

轴承;Floquet理论;倍化分岔;混沌

轴承是机械设备的核心部件，影响着整个设备的运行。而轴承又是极易发生故障的部件之一。当轴承发生故障时，振动行为非常复杂，目前主要研究集中在轴承外圈的振动信号上，对轴承故障面的非线性行为研究较少，而在故障轴承中由碰撞引起的非线性行为又是振动的关键行为，这对轴承的故障诊断和轴承设计有着非常重要的影响。

目前对轴承系统的故障行为主要集中在数值仿真方面。通常根据轴承的力学方程，在正常轴承系统中引入一个故障冲击来模拟故障，相对比较简单、单一，忽略了轴承内部复杂的非线性行为。关贞珍等［1］在正常轴承动力学模型的基础上，考虑轴承局部损伤引起的故障冲击及轴承间隙而引起的非线性接触力变换等因素，建立了轴承局部损伤外圈缺陷、内圈缺陷和滚动体缺陷的动力学模型，利用数值积分对此模型进行了动力学仿真和分析。张建军等［2］根据轴承故障产生机理建立故障轴承动力学模型，引入单元谐振器模拟出现故障后轴承元件的高频固有振动，使用龙格库塔数值积分方法分别对滚动轴承外圈、内圈和滚动体局部故障进行动力学仿真和分析。朱永生等［3］研究滚动轴承结合面间的多体接触与传递过程的耦合作用，建立轴承振动模型，通过数值仿真实现单点、复合故障的有效模拟。曹宏瑞等［4］基于Jones轴承建模理论，建立了高速滚动轴承动力学模型，对滚动轴承单点损伤进行数学描述，将损伤产生的激励力输入轴承模型，利用Newmark－时域积分法对轴承损伤产生的动态振动响应进行了数值仿真。

而在实际轴承发生故障时，滚动体和内外圈之间的作用就会发生相当于含间隙的弹性碰撞，此时的系统是一个非光滑的分段弹性系统。由于滚动体和内圈外圈之间的间隙都非常的小，滚动体很容易发生碰撞而出现非光滑系统的稳定性失稳问题，因此必须考虑碰撞分界面处的非线性振动行为来研究振动机理。目前，国内外学者对碰撞系统的非线性振动行为做了大量的研究。Luo［5－6］研究了一个分段线性周期激励系统，通过建立相应映射，研究各类稳定和不稳定的周期运动，同时对齿轮传动振动的分段线性系统进行了研究，分析了塑性碰撞时该系统的周期运动和稳定性。Ji等［7］考虑了一类由分段弱非线性——线性振子组合而成的周期激励系统，通过施加连续和匹配条件，得到了系统的对称型周期运动。Guckenheimer等［8］对一类在简谐激振力作用下有单侧约束的单自由度振子做了研究，用中心流形定理分析了周期运动的局部分岔，并通过同宿相截条件讨论了混沌运动。Yoshitake和Sueoka［9－10］对不同的不连续系统进行了研究并且给出了不连续分岔的分岔图。Peterka［11］研究了具有粘滞阻尼的碰撞振子中的擦边分岔、周期倍化分岔和鞍结分岔之间的转迁现象。Kleczka等［12］通过对不稳定周期解延续及胞映射方法发现并讨论了含间隙振子中混沌的激变现象。Leine等［13］对非光滑系统周期解的不连续分岔作了进一步的研究，分析了伴随基解矩阵的跳跃而发生的各种不连续分岔现象。曹登庆等［14］系统地综述了空间可展机构非光滑力学建模与非线性动力学的研究进展，介绍了含间隙铰链空间可展机构的非线性动力学特性的稳定性和各类分岔等，提出了空间可展机构非光滑动力系统动力学、稳定性与控制中亟待解决的若干问题。秦志英等［15］根据非光滑映射的分岔理论，基于边界两侧Jacobi矩阵的特征值对非光滑分岔作进一步的分类，并研究经由非光滑分岔通向混沌的路径。罗冠炜等［16］研究了两类含对称刚性约束振动系统的周期运动和分岔，对比了间隙值和激振频率对两振动系统对称碰撞周期运动的稳定性和分岔的影响，分析了对称碰撞周期运动的分岔规律。目前针对故障轴承系统的碰撞面振动的非线性行为研究很少。

本文建立了三自由度轴承内圈故障系统的非光滑模型，将光滑系统的Floquet理论引入到该系统来分析系统周期运动发生倍化分岔的条件。通过在碰撞面处建立Poincaré映射，结合理论分析通过数值方法来进一步揭示故障轴承系统的周期运动经倍化分岔通向混沌的现象。对大型高速旋转机械的安全性、可靠性、故障检测和工业噪音控制等问题的解决具有一定理论指导意义。

1 故障滚动轴承建模分析及运动过程

本文根据轴承实际情况简化了该模型见图1(a)，为了研究当轴承内圈发生故障时，内圈与单个滚动体的碰撞振动的非线性行为，建立了当内圈存在故障的情况下的轴承单个滚动体的碰撞模型见图1(b)。轴承内圈发生破损故障时，滚动体和内圈发生了碰撞接触，属于振冲系统，D为故障深度;同时内圈、外圈与每个滚动体碰撞时，对每个滚动体来说冲击力都是在径向方向振动的，因此轴承单个滚动体分段线性弹性碰撞模型具有一定的合理性。M1，M2，M3分别为内圈与轴的等效质量、滚动体质量、外圈及机座的质量，X1，X2，X3分别为M1，M2，M3的运动的位移;C1，C2，C3分别为M1与M2的阻尼，M2与M3之间阻尼，M3与固定端阻尼，K1，K2，K3分别为三个物体之间的刚度，K4为发生故障时，内圈与滚动体之间的接触刚度。F1sin(Ω1T)，F2sin(Ω2T)分别为作用在M1，M2的等效作用力，Ω1与Ω2分别为转轴和保持架的频率，D为故障深度。

图1 滚动轴承简化模型Fig.1 The simplified rolling bearingmodel

为了描述该轴承系统的运动过程，引入一个分界面，以内圈故障与滚动体刚接触时的碰撞面为分界面如图1距离滚动体为D的平面。由于碰撞面是随M1运动的，所以分界面是移动的，是一个相对固定的分界面，首先定义边界函数，E=X1－X2－D，分界面可表示如下:

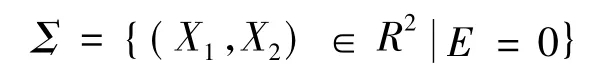
表示物块M1与M2刚接触或分离，这样状态空间被分界面分成两部分(见图2)。

在图2中，V+= {X∈R2E(X1，X2)＞0}为物块与断弹簧K4接触状态;V－={X∈R2E(X1，X2)＜0}为物块与断弹簧K4分离状态。

根据上面的分析，可建立系统的运动学方程为:

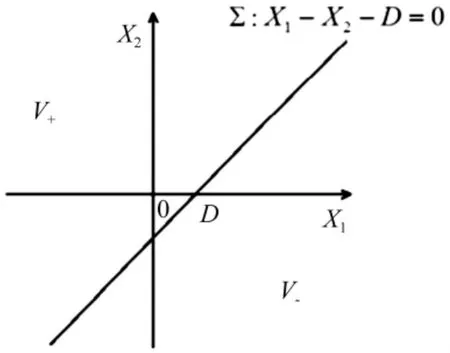
图2 轴承模型二维相平面图Fig.2 The two－dimensional phase plane of bearingmodel

2 系统倍化分岔的Floquet特征乘子分析

设式(5)的一个解x(t)从区域v－出发，即x(t0)∈v－。在t=tp时刻到达分界面Σ。系统在区间B= {t∈Rt0≤t≤tp}是连续的，相应的基解矩阵也是连续的。然而由于向量场f(t，x(t))在分界面处的非光滑性使得相应的Jacobian矩阵在分界面处通常是不连续的，这将引起系统整个基解矩阵不连续，因此在不连续处需要求出相应的切换矩阵。

下面来求分界面处的切换矩阵。

(1)从区域v－进入区域v+时，对超平面Σ:e= x1－x2－d=0，有法向量n=［1，0，1，0，0，0］T，设一周期解x(t)到达分界面Σ的时间为t1并交于点xt1。在t1时刻计算切换矩阵［17］如下

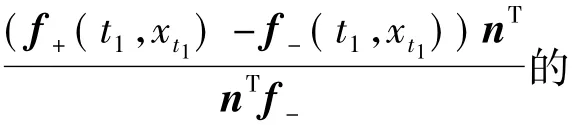
(2)从区域v+进入区域v－，设周期解x(t)到达分界面Σ的时间为t2并交于点x(t2)，在时刻t2有切换矩阵

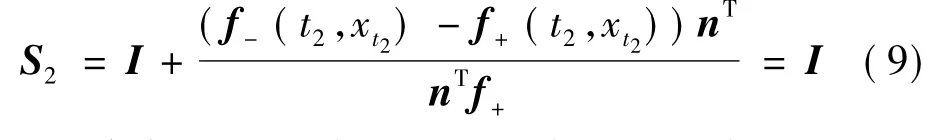
下面求各光滑区域的基解矩阵。在区域v－系统的运动方程为

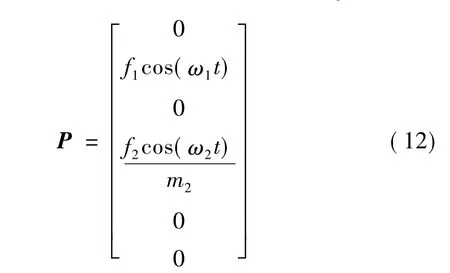
式(10)的扰动在周期解x(t)处线性化系统的基解矩阵为:

同理，在区域v+可求得相应的基解矩阵

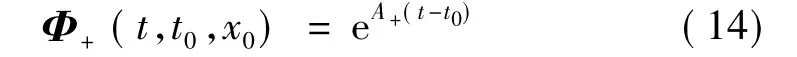
这里，

因为我们研究的是式(5)穿越了分界面的周期解，将切换矩阵式(8)和式(9)结合各子空间相应的基解矩阵式(13)和式(14)经过合成可得全局的单值矩阵:

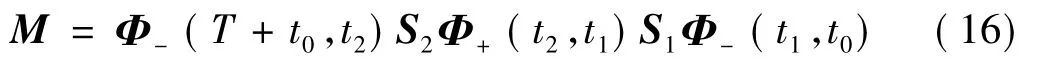
式中:T=2nπ/ω1为系统周期的整数倍，n为自然数;t0为初始时刻，t1和t2分别为轨线到达分界面的两段时间。

于是系统的Floquet特征乘子即为单值矩阵式(15)的特征值。对于式(5)这样的非光滑系统，由于分界面是光滑的，系统的Floquet特征乘子是连续穿越单位圆周的。当有一个Floquet特征乘子沿实轴从(－1，0)穿出单位圆，其它特征乘子仍位于单位圆内时，式(5)稳定的周期解将发生倍化分岔。

3 数值分析

为了通过数值仿真进一步揭示滚动轴承系统式(3)和式(4)的倍化分岔现象以及其它复杂的的动力学行为，在分界面∑处取Poincare截面如下:

式中:θ=ω1t;S=R(mod2π)为1个实数对2π取余数。

选取式(3)和式(4)的一组无量纲化参数:b= 0.001;f1=1;f2=0;m2=1.5;m3=5;ζ1=0.04;ζ2= 0.8;ζ3=0.4;k2=3;k3=4;k4=50。以旋转频率ω1为分岔参数。

当ω1=ωs=2.617 702时(ωs为轴承临界分岔的旋转频率)，轴承故障系统对应的其中一个Floquet特征乘子为λ1(ωs)=－0.999 999 57，接近单位圆周上的(－1，0)点;其它的特征值

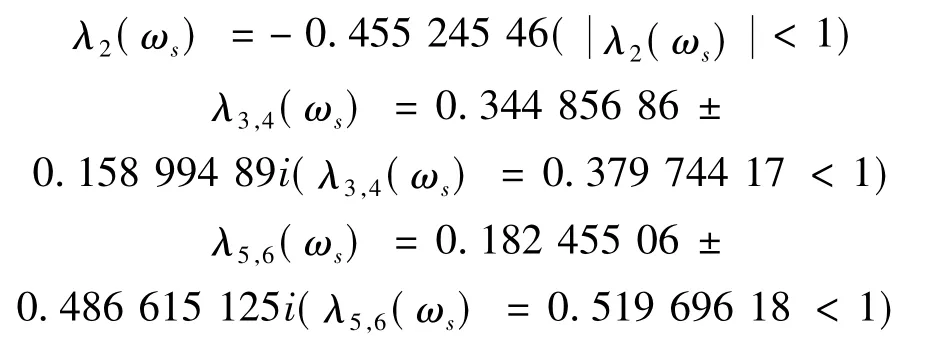
仍在单位圆周内。由此可见轴承内圈故障系统在ω1=ωs=2.617 702时发生了倍化分岔。系统随ω1变化的分岔图(见图3和图4)。

图3 系统的分岔图Fig.3 The bifurcation diagram of the system

图4 系统的倍化分岔图局部放大Fig.4 Themagnification of period－doubling bifurcation diagram

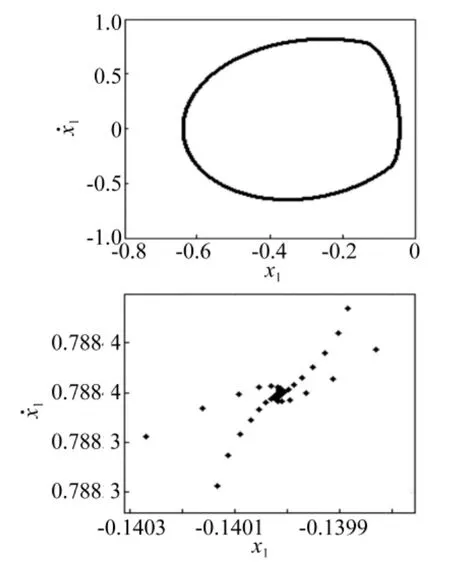
图5 ω1=2.59时单周期运动的相图和庞加莱截面图Fig.5 The phase diagram and poincare section diagram of single periodic motion atω1=2.59

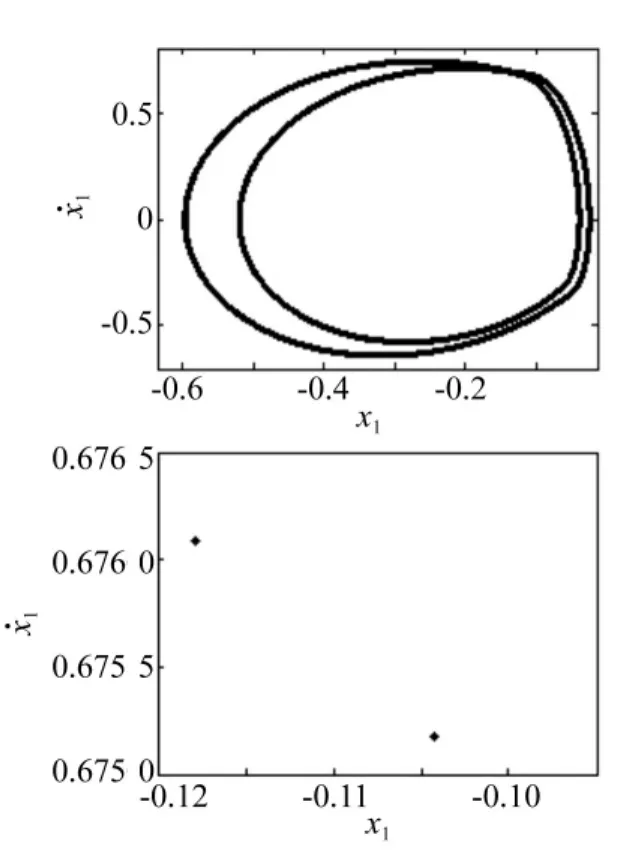
图6 ω1=2.695时周期二运动的相图和庞加莱截面图Fig.6 The phase diagram and poincare section diagram of period 2 motion atω1=2.695

图7 ω1=2.99时拟周期运动的相图和庞加莱截面图Fig.7 The phase diagram and poincare section diagram of quasi－periodic motion atω1=2.99

图8 ω1=3.05时相图和庞相莱截面上的锁相Fig.8 The phase diagram and phase locked state on poincare section atω1=3.05

由图3和图4可知，系统起初处于稳定的单周期运动(见图5)。当ω1=ωs=2.617 702时系统经历倍化分岔并过渡到周期二运动(见图6)，随着旋转频率ω1的增加，ω1=2.99时系统的庞相莱截面是两个圈，说明系统与碰撞面最后收敛于这两个圈上，发生了周期二解的Nermark－Sacker分岔(见图7)，当ω1=3.05时系统的庞相莱截面由两个圈变得不再规则，变成了锁相状态，相图和庞相莱截面图(见图8)，随着ω1的增加，系统进入了周期三运动，其庞相莱截面图(见图9)，ω1的继续增加，系统又转入单周期运动(见图10)，在系统经历一个较长的单周期运动后，随着ω1的增加，系统经历了各种周期运动和混沌相间的非线性动力学行为，其庞相莱截面图(见图11～图15)。

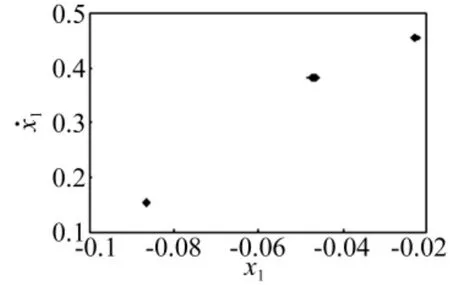
图9 ω1=3.3时周期三运动的庞加莱截面图Fig.9 The poincare section diagram of period 3 motion atω1=3.3

图10 ω1=4时单周期运动庞加莱截面图Fig.10 The poincare section diagram of single periodicmotion atω1=4

图11 ω1=4.8时周期二运动的庞加莱截面图Fig.11 The poincare section diagram of period 2 motion atω1=4.8

图12 ω1=5时混沌运动的庞加莱截面图Fig.12 The poincare section diagram of period 2 motion atω1=5

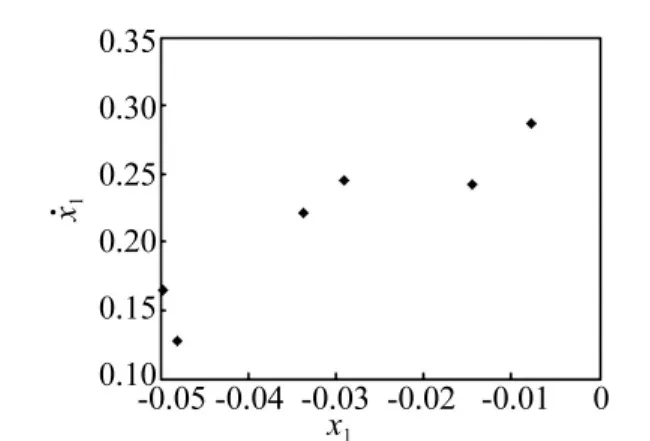
图13 ω1=5.2时多周期运动的庞加莱截面图Fig.13 The poincare section diagram of multiple periodic motion atω1=5.2

图14 ω1=5.23时混沌运动的庞加莱截面图Fig.14 The poincare section diagram of chaosmotion atω1=5.23

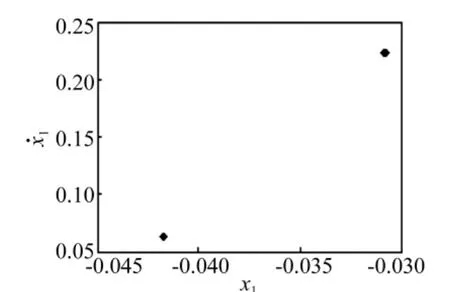
图15 ω1=5.7时周期二运动的庞加莱截面图Fig.15 The poincare section diagram of period 2 motion atω1=5.7

4 结论

本文建立了轴承内圈发生破损故障时的三自由度分段非光滑模型，计算了切换矩阵，结合光滑系统的Floquet理论分析了该系统周期运动发生倍化分岔的条件。数值仿真验证了理论分析的正确性并进一步揭示了系统的周期倍化现象以及周期二运动的Nermark－Sacker分岔、多周期和混沌等复杂的非线性行为。

［1］关贞珍，郑海起，王彦刚，等.滚动轴承局部损伤故障动力学建模及仿真［J］.振动、测试与诊断，2012，32(6):950－956.

GUAN Zhen－zhen，ZHENG Hai－qi，WANG Yan－gang，et al.Fault dynamic modeling and simulating of rolling bearing with localized defect［J］.Journal of Vibration，Measurement＆Diagnosis，2012，32(6):950－956.

［2］张建军，王仲生，芦玉华，等.基于非线性动力学的滚动轴承故障工程建模与分析［J］振动与冲击，2009，29(11):30－34.

ZHANG Jian－jun，WANG Zhong－sheng，LU Yu－hua，et al.Nonlinear dynamic modeling for localized defects in a rolling element bearing［J］.Journal of Vibration and Shock，2009，29 (11):30－34.

［3］朱永生，袁幸，张优云，等.滚动轴承复合故障振动建模及Lempel－Ziv复杂度评价［J］.振动与冲击，2013，32(16):23－29.

ZHU Yong－sheng，YUAN Xing，ZHANG You－yun，et al.Vibration modeling of rolling bearings considering compound multi－defect and appraisal with Lempel－Ziv complexity［J］.Journal of Vibration and Shock，2013，32(16):23－29.

［4］曹宏瑞，牛蔺楷，何正嘉.高速主轴轴承损伤建模与振动响应仿真研究［J］振动与冲击，2012，31(增刊1):241－244.

CAO Hong－rui，NIU Lin－kai，HE Zheng－jia.Bearing defects modelling and vibration response simulation of high－speed spindle systems［J］.Journal of Vibration and Shock，2012，31 (Sup1):241－244.

［5］Luo A C J.The mapping dynamics of periodic motions for a three piecewise linear system under a periodic excitation［J］.Journal of Sound and Vibration，2005，283:723－748.

［6］Luo A C J，Che L.Periodic motions and grazing in a harmonically forced，piecewise，linear oscillator with impacts［J］.Chaos，Solitons and Fractals，2005，24:567－578.

［7］Ji JC，Hansen C H.Analytical approximation of the primary resonance response of a periodically excited piecewise nonlinear－linear oscillator［J］.Journal of Sound and Vibration，2004，278:327－342.

［8］Guckenheimer J，Holmes P.Nonlinear oscillations，dynamical systems and bifurcations of vector fields［M］.New York: Springer－Verlag，1983.

［9］Yoshitake Y，Sueoka A.Forced self－exited vibration accompanied by dry friction.Applied nonlinear dynamics and chaos of mechanical systems with discontinuities［J］.World Scientific Series on Nonlinear Science Series A，2000，28:237－259.

［10］Yoshitake Y，Sueoka A，Shoji N，et al.Vibrations of nonlinear systems with discontinuities.The case of the preloaded compliance system［J］.Japan Society Mechanical Engineering (JSME)Series，1997，41(4):710－717.

［11］Peterka E Bifurcation and transition phenomena in an impact oscillator［J］.Chaos，Solitons and Fractals，1996，7(10): 1635－1647.

［12］Kleczka M，kreuzer E，Wilmers C，et al.Nonlinear dynamics in engineering systems［M］.Berlin:Springer－Verlag，1990.

［13］Leine R I，Nijmeijer H.Dynamics and bifurcation of nonsmooth mechanical systems［M］.Berlin:Springer，2004.

［14］曹登庆，初世明，李郑发，等.空间可展机构非光滑力学模型和动力学研究［J］.力学学报，2013，1:3－15.

CAO Deng－qing，CHU Shi－ming，LIZheng－fa，et al.Study on the non－smooth mechanical models and dynamics for space deployable mechanisms［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，1:3－15.

［15］秦志英，陆启韶.非光滑分岔的映射分析［J］.振动与冲击，2009，28(6):79－82.

QIN Zhi－ying，LU Qi－shao.Map analysis for non－smooth bifurcations［J］.Journal of Vibration and Shock，2009，28(6):79－82.

［16］罗冠炜，张艳龙，谢建华.含对称刚性约束振动系统的周期运动和分岔［J］.工程力学，2007，24(7):44－53.

LUO Guan－wei，ZHANG Yan－long，XIE Jian－hua.Periodicimpact motions and bifurcations of vibratory systems with symmetrical rigid constraints［J］.Engineering Mechanics，2007，24(7):44－53.

［17］Leine R I，Nijmeijer H.Dynamics and bifurcation of nonsmoothmechanical systems［M］.Berlin:Springer，2004.

Period-doubling bifurcation of a rolling bearing system w ith inner race fault

WANGQiang1，LIU Yong－bao1，XU Hui－dong2，HE Xing1，LIU Shu－yong1
(1.College of Power Engineering，Naval University of Engineering，Wuhan 430033，China;
2.Key Laboratory of Marine Power，Wuhan 430033，China;
3.College of Mechanics，Taiyuan University of Technology，Taiyuan 030024，China)

A piecewise non－smooth model with 3－DOF for a rolling bearing system with inner race fault was established.The period－doubling bifurcation and chaos of the bearing system were studied here.After the switchmatrixes of the system were solved，the period－doubling bifurcation condition of the non－smooth bearing system was analyzed by combining the switchingmatrixeswith Floquet theory for smooth systems.The numericalmethod was used to further reveal the period－doubling bifurcation and chaos of the bearing system through estabilshing Poincare mapping in the collision plane.The results showed that when the rotating frequency is close to the critical bifurcation point，one of Floquet multipliers of the system is close to－1，and its period－doubling bifurcation appears;with increase in rotating frequency，the system experiences Nermark－Sacker bifurcation of the period 2 solution，and then experiencesmore complex nonlinear behaviors，such as，multi－periodic solutions and chaos.Studying bifurcation and chaos of fault bearing systems provided a reliable basis for their design and fault diagnosis and provided theoretical guidance and technical support for their actual design in safe and stable operation of large high－speed rotatingmachineries.

bearing;floquet theory;period－doubling bifurcation;chaos

TH212;TH213.3

A

10.13465/j.cnki.jvs.2015.23.024

国家自然科学基金项目(51179197，11002052);国家海洋工程重点实验室(上海交通大学)基金资助项目(1009)

2014－09－03修改稿收到日期:2014－11－26

王强男，博士生，1985年生

刘永葆男，教授，博士生导师，1967年生邮箱:yongbaoliu_wq@163.com