随机敏感度函数法在非自治非线性系统中的应用

郭空明，江俊

(1.西安电子科技大学机电工程学院，西安710071;2.西安交通大学机械结构强度与振动国家重点实验室，西安710049)

随机敏感度函数法在非自治非线性系统中的应用

郭空明1，江俊2

(1.西安电子科技大学机电工程学院，西安710071;2.西安交通大学机械结构强度与振动国家重点实验室，西安710049)

研究非自治微分动力系统周期吸引子受弱高斯白噪声扰动后的分布特性。基于频闪映射将微分动力系统离散为映射，通过求解映射系统周期吸引子的随机敏感度函数，构造置信椭圆来刻画随机吸引子的分布情况，从而避免了求解矩阵微分方程的边值问题，只需求解矩阵代数方程即可。研究了Duffing方程随机周期吸引子的分布情况，结果表明置信椭圆与Monte－Carlo模拟取得了很好的一致。最后对Duffing方程的噪声诱导混沌现象进行了定性研究，证明了通过随机敏感度函数可以揭示这类现象的机理。

随机敏感度函数;频闪映射;Duffing方程;噪声诱导混沌

实际宏观动力系统的建模往往是简化的。当一些状态，尤其是快变的状态难以用确定性方程进行描述时，往往将这些状态孤立于系统模型之外，基于其统计特性，将其视为对系统模型的随机扰动。因此，针对实际动力系统建立的模型总是不可避免地受到随机扰动(又称噪声)的影响。

由于随机扰动带来的扩散作用，动力系统的状态最终会遍布整个相空间，因此，理论上随机动力学问题是一个全局问题。受高斯白噪声扰动的动力系统作为Markov过程，其概率密度演化满足Fokker－Planck－Kolmogorov方程(对于微分动力系统)或Frobenius－Perron积分方程(对于离散映射系统)。

但即使对于简单的动力系统这两种方程都很难求出精确解。为了用数值或近似解析方法得到全局概率密度分布，国内外已进行了大量工作。例如，朱位秋等［1］建立了一类随机振动系统的拟哈密顿理论框架，可以解决随机分岔、首次穿越以及随机最优控制等诸多问题。徐伟等［2］使用广义胞映射、路径积分、正交多项式展开等方法对非线性随机动力系统进行了研究。对于随机结构的振动，李杰等［3］提出了概率密度演化方法，等。

另一方面，对于受到弱高斯白噪声扰动的系统，当系统的初始概率密度集中于吸引子附近时，概率密度在达到全局稳态分布之前，会在吸引子附近形成一个持续很长时间的准稳态分布。由于观测时间往往是有限的，对于这类系统可以进行局部分析，认为系统的响应只是对原确定性系统吸引子的一种局部扰动，并将这种准稳态分布称为随机吸引子(见图1)。

由于很多由噪声诱导的复杂现象，如随机分岔［4］、噪声诱导同步［5］等都是因吸引子受扰而产生，因此，如何对各种吸引子在噪声扰动下的局部扩散行为进行定量估计，是一个突出的问题。针对该类问题，Bashkirtseva和Ryashko［6］提出了随机敏感度函数的概念，通过求解不动点或周期吸引子的随机敏感度函数，可以得到随机吸引子的协方差矩阵，还可以构造置信椭圆对系统响应范围进行刻画。与其它方法相比，这种方法简单易用，计算量很小。目前这种方法在微分动力系统和映射系统中都得到了广泛应用，并且可以解释一些噪声诱导的复杂现象［7］。

映射系统的随机敏感度函数满足矩阵代数方程，而微分动力系统随机敏感度函数的求解是一个矩阵微分方程的边值问题。Bashkirtseva等提出了两种迭代的方法来求解微分动力系统的随机敏感度函数。本文基于非自治系统的特点，利用频闪映射的方法将微分动力系统离散为映射，通过求解该映射系统的随机敏感度函数，估算系统在特定时刻的响应分布。这种方法避免了迭代求解矩阵微分方程边值问题，只需求解矩阵代数方程即可。

图1 随机不动点吸引子Fig.1 Stochastic fix point attractor

1 映射系统的随机敏感度函数

考虑如下的受扰映射系统:

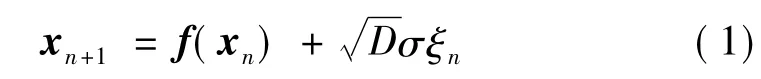
式中:x为N维矢量，f为N维矢量函数，σ为N×M维噪声输入矩阵，ξn代表M维高斯噪声矢量，满足:

式中:E为数学期望，I为单位矩阵。

首先考虑不动点吸引子。假设式(1)存在一个指数稳定的不动点则该吸引子的随机敏感度函数为一N×N维矩阵W，满足如下的矩阵代数方程:

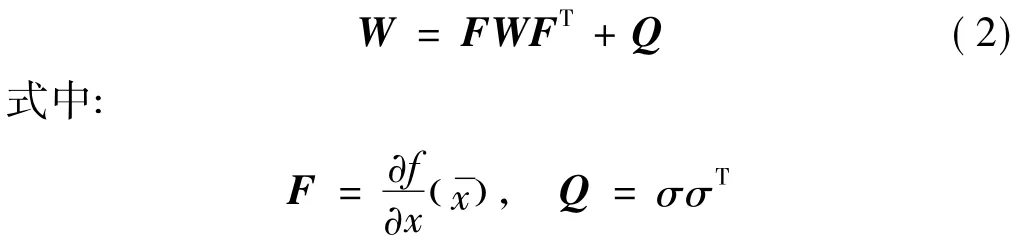
而随机不动点吸引子对应的协方差矩阵为D W。随机吸引子的分布情况为高斯分布，可以用置信椭圆来刻画，置信椭圆的表达式为:

式中:χ2P为自由度为N的卡方分布在累积概率密度为P时，累积分布函数的反函数。P同时也为置信椭圆的置信度，表示随机吸引子上的点落入置信椭圆的概率为P，一般取为一个接近于1的值。

采用压缩映射的方法，可将周期k吸引子压缩为周期1。不失一般性，在周期点1处进行压缩，将式(5)连续应用k次，结合式(6)，可以得到压缩映射中的不动点，也就是周期点1的随机敏感度函数满足的矩阵方程:

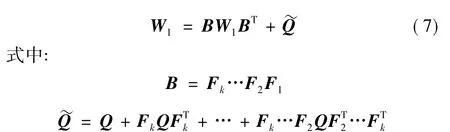
求解得到W1之后，由式(5)可进一步得到其它k－1个周期点的随机敏感度函数。而每个周期点处的置信椭圆满足方程:

2 非自治微分动力系统的随机敏感度函数

考虑如下的非自治微分动力系统:

式中:f(x，t)为N维非定常矢量场。从时刻t0处出发，可以构造一系列时间间隔为Δt的频闪截面:

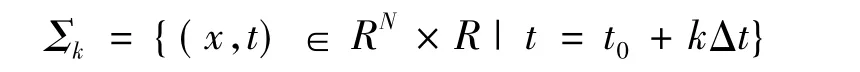
这些截面将式(9)离散为映射:

式中:φt(x)为f(x，t)生成的流。

若令时间间隔Δt→0，则式(10)可写成显式:

为t0+kΔt时刻对应状态下的Jacobi矩阵。

则周期为T的周期吸引子离散为映射系统式(11)的周期N吸引子(见图2):

图2 频闪映射Fig.2 Stroboscopic map

下面考虑受高斯白噪声扰动的系统:

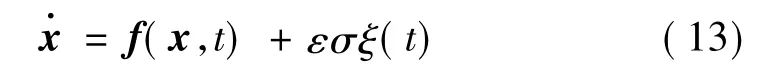
利用频闪截面离散方法以及欧拉－丸山积分法，可将式(13)的映射系统表达为:

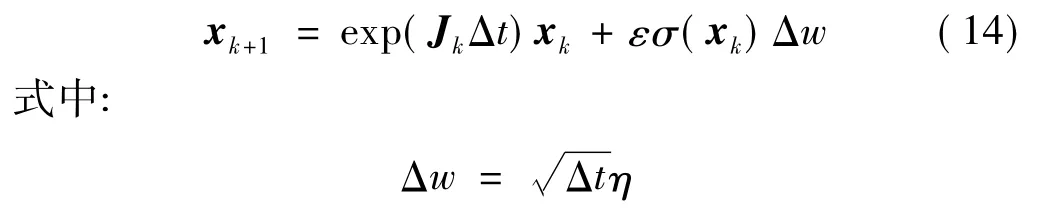
表示时间间隔［t0+kΔt，t0+(k+1)Δt］中维纳过程的增量，η服从高斯分布。

利用映射系统周期吸引子随机敏感度函数的求解方法求解映射系统式(14)，便可求出随机周期吸引子在各频闪截面上的分布情况。

这里将Δt=T/N时间间隔内非线性的映射式(10)近似为线性映射式(11)，相当于将一个周期T内连续的周期轨道用N段直线逼近。虽然此时式(4)～式(7)中的各矩阵Fi以及矩阵B均为近似值，但当N足够大，Δt→0时，误差就忽略不计。

3 Duffing方程周期解的受扰特性研究

3.1 Duffing方程周期解的受扰分布

研究如下受随机扰动的双势阱Duffing方程［9］:

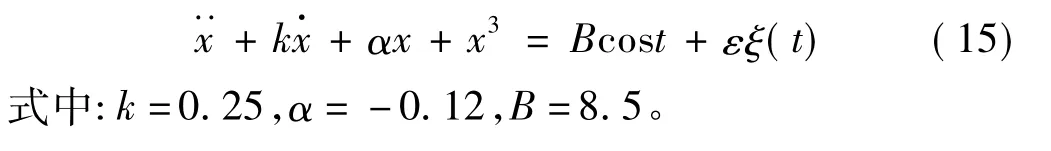
传统的方法是取周期与激励周期2π相同的频闪截面来观察系统的全局特性。扰动强度ε=0时，系统存在一个周期三吸引子(三角形)，一个混沌鞍(见图3)。

下面考虑小噪声扰动的情况。取式(12)中的N= 300，由于吸引子的周期为6π，因此Δt=0.02π。计算出三个周期点的随机敏感度函数W之后，取噪声强度ε=0.03，置信概率P=99.99%，利用式(8)，可以分别画出三个周期点的置信椭圆(见图4)。为了验证方法的有效性，利用欧拉－丸山积分法对方程(15)进行了Monte－Carlo模拟，从图4可知，随机吸引子的分布与置信椭圆有很好的一致性。

为了讨论频闪截面时间间隔Δt与计算结果的关系，在图5中画出N=50，150，100，200四种情况下，图4最上方的置信椭圆。可以看出当N=100时，由于频闪截面时间间隔太大，误差还比较大，画出的置信椭圆与其它三种N取值下的置信椭圆明显不同，而当N= 200，300和400时，椭圆的形状和大小就区别不大了。因此对于本例，N=300计算出的结果是可靠的。

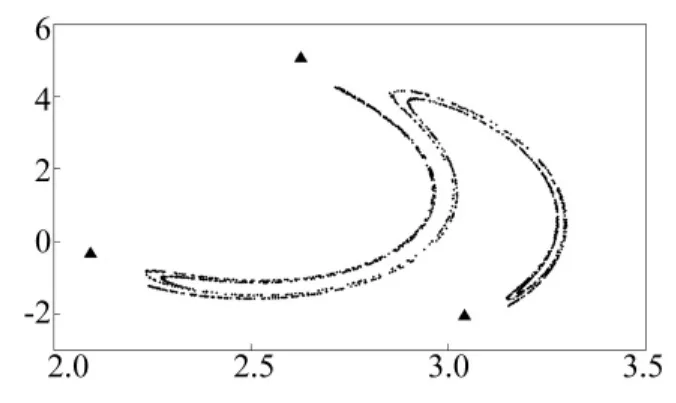
图3 Duffing方程的全局特性Fig.3 Global character of Duffing equation

图4 ε=0.03时Duffing方程的随机响应Fig.4 Stochastic response of Duffing equation whenε=0.03

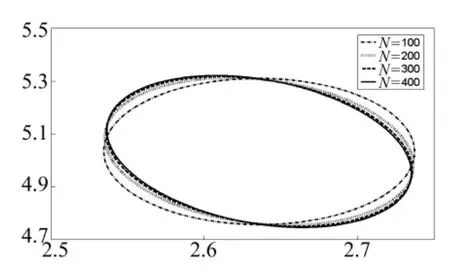
图5 N取不同值时的置信椭圆Fig.5 Confidence ellipses with different N

3.2 Duffing方程的噪声诱导混沌

对于“噪声诱导混沌”这一名词的适用范围目前学术界还未有一致性结论，但对于噪声诱导下轨道访问混沌鞍这种情形，由于响应中本来就包含混沌不变集，因此将这类现象称为噪声诱导混沌是没有异议的。一些学者建议将其命名为“噪声揭示混沌”［10］。

当噪声进一步增大时，Duffing系统将出现噪声诱导混沌现象。图6给出了ε=0.05时系统的响应。可以看出此时的响应是由随机周期三吸引子和混沌鞍组成，置信椭圆已无法精确给出状态的分布。图7给出了系统最大Lyapunov指数随噪声强度的变化，可以看出，随着噪声强度逐渐增大，系统最大Lyapunov指数也逐渐增大，这是因为随噪声强度的增大，轨道访问混沌鞍愈发频繁，混沌响应的比例逐渐增大。

为了揭示噪声诱导混沌的机理，采用两尺度的全局分析法［11］，将周期三吸引子(三角形)及其置信椭圆(噪声强度ε=0.05，P=99.99%)与混沌鞍的稳定流形、不稳定流形同时画出(见图8)。可以看出，噪声诱导下随机吸引子与混沌鞍的稳定流形相碰撞，沿着稳定流形到达混沌鞍，再沿着混沌鞍的不稳定流形离开，这与Tél等［12］的结论一致。

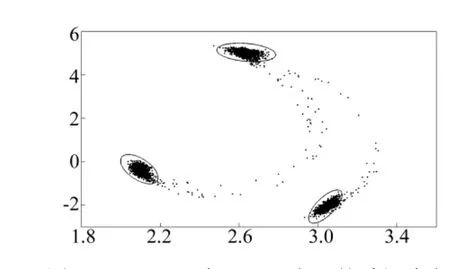
图6 ε=0.05时Duffing方程的随机响应Fig.6 Stochastic response of Duffing equation whenε=0.05

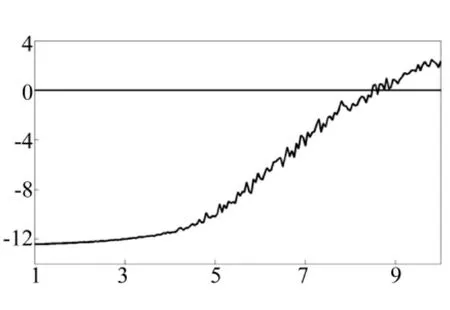
图7 最大Lyapunov指数随噪声强度的变化Fig.7 Change of largest Lyapunov exponentwith noise strength

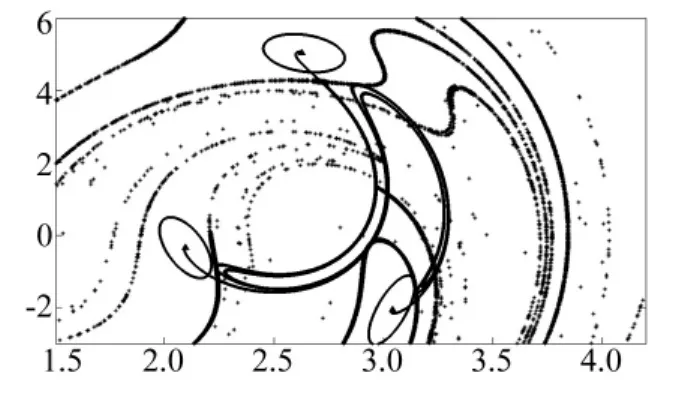
图8 置信椭圆与混沌鞍稳定流形的碰撞Fig.8 Collision of confidence ellipses with stablemanifold of chaotic saddle

4 结论

本文采用频闪映射的方法，将连续时间系统转换为映射并采用随机敏感度函数的方法估算系统在频闪截面上的响应分布。方法的有效性通过一类受加性高斯白噪声扰动的受迫Duffing方程得到验证。最后还使用随机敏感度函数对Duffing方程的噪声诱导混沌现象进行了机理研究。

随机敏感度函数法虽然已经有了大量应用，但还有一些重要的工作需要进一步研究，例如如何量化该方法的适用噪声范围，以及置信椭圆的置信概率如何根据问题实际需要的可靠性加以确定等。

［1］朱位秋.非线性随机动力学与控制:Hamilton理论体系框架［M］.北京:科学出版社，2003.

［2］徐伟.非线性随机动力学的若干数值方法及应用［M］.北京:科学出版社，2013.

［3］刘章军，李杰.基于概率密度演化理论的结构抗震可靠性分析［J］.振动与冲击，2009，28(9):1－4.

LIU Zhang－jun，LI Jie.A seismatic reliability analysis of nonlinear structures based on probability density evolution method［J］.Journal of Vibration and Shock，2009，28(9):1－4.

［4］高喆，秦卫阳，梁晓鹏，等.碰摩转子－轴承系统的随机分岔与混沌特性分析［J］.振动与冲击，2013，32(20):161－164.

GAO Zhe，QIN Wei－yang，LIANG Xiao－peng，et al.Stochastic bifurcation and chaos analysis of a rub－impact rotor－bearing system.［J］.Journal of Vibration and Shock，2013，32(20):161－164.

［5］杨晓丽，孙中奎.关于非自治Duffing－Van Der Pol混沌系统完全同步的研究［J］.振动与冲击，2010，29(11):131－134.

YANG Xiao－li，SUN Zhong－kui.Research on complete synchronization of non－autonomous chaotic Duffing－Van Der Pol systems.［J］.Journal of Vibration and Shock，2010，29 (11):131－134.

［6］Bashkirtseva IA，Ryashko L B.Stochastic sensitivity of 3D－cycles［J］.Mathematics and Computers in Simulation，2004，66(1):55－67.

［7］Bashkirtseva I A，Ryashko L B.Constructive analysis ofnoise－induced transitions for coexisting periodic attractors of the Lorenz model［J］.Physical Review E，2009，79 (4):041106.

［8］Bashkirtseva I A，Ryashko L B，Tsvetkov I N.Sensitivity analysis of stochastic equilibria and cycles for the discrete dynamic systems［J］.Dynamics of Continuous，Discrete and Impulsive Systems，Series A:Mathematical Analysis，2010，17:501－515.

［9］Hsu C S.Cell－to－cell Mapping:A method of global analysis for nonlinear systems［M］.Berlin:Springer，1987.

［10］Dennis B，Desharnais R A，Cushing JM，et al.Can noise induce chaos?［J］OIKOS，2003，102:329－339.

［11］Jiang J.An effective numerical procedure to determine saddle－type unstable invariant limit sets in nonlinear systems［J］.Chinese Physics Letters，2012，29(5):050503.

［12］Tél T，Lai Y C，Gruiz M.Noise－induced chaos:a consequence of long deterministic transients［J］.International Journal of Bifurcation and Chaos，2008，18(2):509－520.

Application of stochastic sensitivity function method in non-autonomous nonlinear systems

GUO Kong－ming1，JIANG Jun2
(1.School of Mechanic－Electronic Engineering，Xidian University，Xi'an 710071，China;
2.State Key Laboratory for Strength and Vibration，Xi'an Jiaotong University，Xi'an 710049，China)

Distribution characters of periodic attractors in non－autonomous differential dynamic systems disturbed by weak Gaussian white noise were studied.Based on stroboscopic mapping，differential dynamic systems were discretized into maps.Through solving stochastic sensitivity functions of periodic attractors in maps，confidence ellipses were constructed to describe the distributions of random attractors.In this way，solving boundary value problems of matrix differential equationswas avoided，and only matrix algebraic equations needed to be solved.Distributions of stochastic periodic attractors in Duffing equation were studied.The results showed that confidence ellipses achieve a good agreement with Monte－Carlo simulation.Finally，noise－induced chaos in Duffing equation were investigated qualitatively，it was shown that stochastic sensitivity functions can reveal themechanism of this kind of phenomena.

stochastic sensitivity function;stroboscopic map;duffing equation;noise－induced chaos

O313

A

10.13465/j.cnki.jvs.2015.23.021

国家自然科学基金重点项目(11332008);中央高校基本科研业务费专项资金项目(K5051304012)

2014－11－06修改稿收到日期:2014－12－30

郭空明男，博士，讲师，1985年生邮箱:kmguo@xidian.edu.cn