弹性约束浅拱的内共振非线性模态

曾有艺，易壮鹏

(长沙理工大学土木与建筑学院，长沙410114)

弹性约束浅拱的内共振非线性模态

曾有艺，易壮鹏

(长沙理工大学土木与建筑学院，长沙410114)

动力系统采用弹性约束时自振特性、非线性模态与采用理想边界时存在差异，约束刚度值将改变各种非线性动力行为产生的参数域。采用多尺度法进行直接摄动构造了一端竖向弹性约束浅拱在发生2∶1内共振时的非线性模态。结果表明:内共振非线性系统存在单模态运动和耦合模态运动;弹性约束的存在及不同取值将导致不同的非对称线性模态、形函数及内共振激发条件;不同约束刚度时非线性模态的时空效应呈现不同的动力形态。

弹性约束;浅拱;非线性模态;2:1内共振;多尺度法

拱结构受力性能良好，在土木、机械和航空航天等领域应用广泛，研究人员［1－3］对各种外荷载下的运动稳定性和分岔行为进行了系统而深入的研究。在系杆拱桥、弹性约束机械拱臂/曲梁等结构中，基础变形及与相邻结构共同作用引起的附加惯性力将影响精确的动力分析，此时将边界考虑为弹性约束更加合理。因此，Xu等［4］研究了弹性约束拱的动力跳跃特性;Lacabonana等［5］分析了转动弹性约束浅拱的非线性行为;康婷等［6］研究了水平弹性支撑圆拱的动力特性。

非线性模态的概念由Rosenberg［7］提出，其定义与构造［8－11］是非线性振动研究中的基本问题。内共振系统的耦合非线性模态具有分岔行为，且随着系统参数发生变化，导致模态数目超过系统的自由度数，具有显著的非线性特性，因而引起很多研究者的兴趣。如，Nayfeh等［12］采用多尺度法研究了两端固支屈曲梁在发生1∶1和3∶1内共振条件下的非线性模态;Li等［13］构造了一类3对纯虚根1∶2∶5双重内共振系统的非线性模态并分析了其分岔特性;Mamandi等［14］采用四种方法构造并研究了非线性弹性地基上轴向压缩简支梁3∶1内共振条件下的非线性模态。

针对一端竖向弹性约束浅拱，在线性模态、形函数中考虑约束刚度值，通过多尺度法进行摄动分析构造2:1内共振的非线性模态，并分析内共振激发条件及非线性模态的时空效应。

1 动力学模型

式(1)中对应线性系统自由振动的解的一般形式为u(x，t)=φ(x)eiωt，其中ω为自振频率，φ(x)为模态，当ψ=(b/2)(1－cos2πx)且b为矢高时，模态形状为:

图1 一端竖向弹性约束浅拱结构示意图Fig．1 Schematic diagram of shallow arch with oneend vertically elastically constrained

2 摄动分析与非线性模态

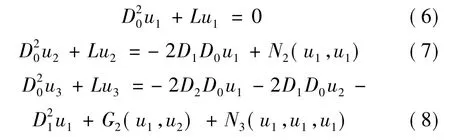
式中:G2(u1，u2)=N2(u1，u2)+N2(u2，u1)是为进一步化简的微分算子，对于n，m阶模态之间的2:1内共振，引入调谐参数σ使得ωn=2ωm+εσ，式(6)的一次近似解可表示为

式(21)和式(24)分别为两种情况下的非线性模态，对具有一定约束刚度的弹性约束浅拱，可以依次按照线性模态、形函数、平均方程系数、非线性模态的顺序进行求解。

3 数值分析

采用数值方法计算k取1 000、10 000和→∞三种情况下的线性模态与频率的分布规律，并以最低两阶模态(m=1，n=2)之间的2∶1内共振为例来分析内共振解及非线性模态的时空效应。

3.1 线性模态与频率

图2给出了三组k值情况下前五阶频率ω随矢高b的变化图，其中实、虚线分别表示奇、偶数阶频率，k=1 000和10 000为典型的弹性约束边界，而k→∞可视为固支边界。可知b在(0，20］内单调增加时，弹性约束浅拱(图2(a)，图2(b))不同阶次频率在相互接近(可能发生1∶1内共振)时发生模态交叉，固支浅拱(图2(c))的频率则发生模态交叉。模态接近方式及k值的不同导致可能发生内共振时的b值出现差异，如图2中出现模态频率为2∶1整数比的b1(1～2阶)、b2(2～3阶)、b3(3～5阶)。另一方面，对比图2(a)，图2(b)，图2(c)可以发现在k增大的过程中各阶频率均增大。

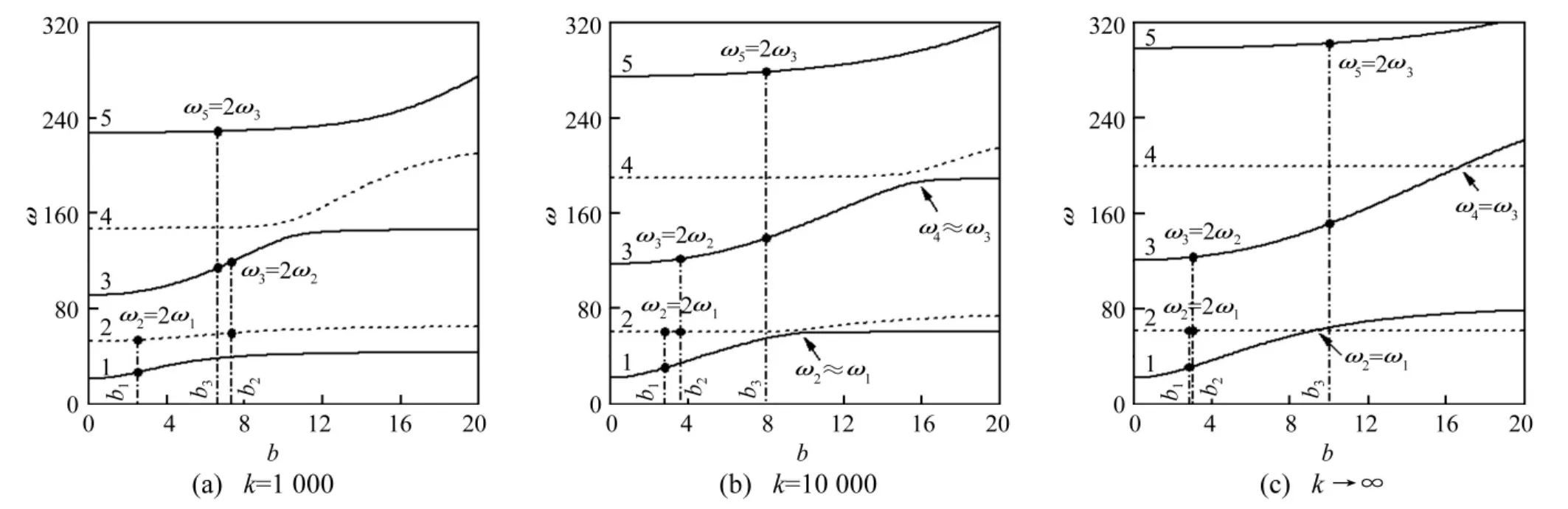
图2 弹性约束浅拱的频率分布图Fig.2 Variation of frequencies for elastically constrained shallow arch

图3 b=b1时前6阶模态分布图Fig.3 The first sixmodes at b=b1

为了进一步验证，图3给出了不同k对应的b=b1时的前6阶线性模态，可知标准化的线性模态沿跨径不对称分布，同时弹性约束端的值不为零，这与固支浅拱(k→∞)的正、反对称模态完全不同。弹性约束浅拱中这些模态的不对称性将导致后续平均方程系数不一致及发生内共振的条件出现变化，这也是弹性约束浅拱与对称的铰支/固支浅拱［16］的不同之处。

3.2 内共振解

形函数直接决定系统的非线性模态，图4给出了k取1 000、10 000和→∞三种情况下形函数Γi(x)(i= 1～6)的分布图，由图4可知，竖向约束刚度对形函数的形状起到主导作用。当k=1 000、10 000时，形函数既非正对称也非反对称(图4(a)～图4(f));而k→∞时Γ1(x)～Γ4(x)正对称(图4(g)～图4(i))，Γ5(x)，Γ6(x)反对称(图4(h))。式(13)中Γi(x)(i=1～6)与内共振模态φm，φn和拱轴线形ψ有关，其形状影响形函数的分布。另外，由图4还可发现各形函数弹性约束端的值不为零，且通过对比可知端值大小随着k的增大而变小，直至k→∞时变为零。

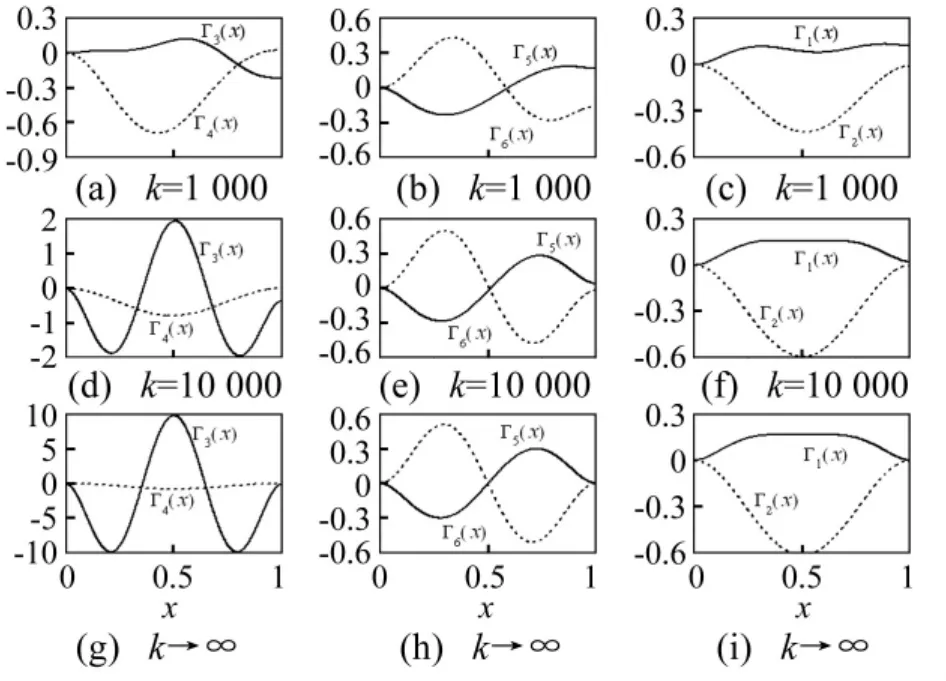
图4 b=b1时形函数Γi(x)图Fig.4 Shape functionsΓi(x)at b=b1

表1给出了b=b1时平均方程式(17)中系数Sij和S1的计算结果，这些系数与m，n阶频率、模态及拱轴线形有关。值得指出的是S1随着k的增大而减小，最终(k→∞)为零，也即弹性约束时不等于零，刚性约束时等于零。实际上这是最低两阶模态之间的2∶1内共振是否被激发的判定条件:浅拱一端为竖向弹性约束时两模态间的2∶1内共振被激发;当约束为刚性(k→∞)时，虽然两阶频率的比值为2∶1，但是不会发生内共振(S1=0导致)。这也是浅拱由于边界条件不同所致动力特性方面的显著不同之处。

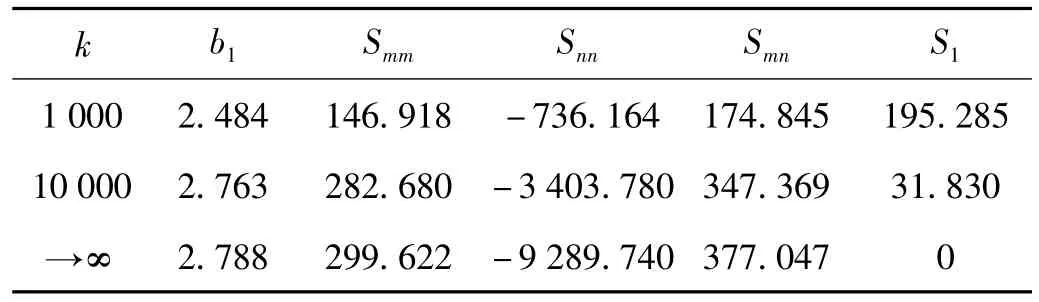
表1 b=b1时2∶1内共振平均方程系数Tab.1 Coefficients ofmodulation equation for 2∶1 internal resonance at b=b1

图5给出了最低两阶模态之间发生2∶1内共振时非线性模态的幅值和频率分布。图5(a)所示为k取不同值时单模态解中an与σ的关系，实际上也可令式(20)右边大括号内的项等于零得到图5(a)中每一个k值对应曲线的上支和下支，由单模态解的特征值判断可知两支曲线之间的部分为内共振解的不稳定区，两支曲线以外的部分则为稳定区。另外，不稳定区的分布随着k的增大而减小，直至k→∞为零，曲线的上、下支重合。

图5(b)和图5(c)分别给出了k=1 000、10 000时耦合模态解中am－an和am－ωmN/ωm关系曲线，k→∞时S1=0系统无内共振解，另外由于ωnN≈2ωmN，图5 (c)中仅给出了am与通过线性频率ωm标准化之后的ωmN的关系图。两阶模态发生内共振的相互作用时，非线性系数Sij由分别负责软、硬弹簧性质的2阶、3阶效应两部分组成，Sij在k的增大过程中符号不发生变化，但是绝对值均增大，导致对于某一给定的an值，am的大小随着k的增大而增大(见图5(b))。图5(c)中am－ωmN/ωm曲线呈现硬弹簧性质，且k增大这种特征减弱，这是由于在ωmN的标准化表达式中，对于给定的an，σ和γ随着k的增长Sij使ωmN呈软化特性。

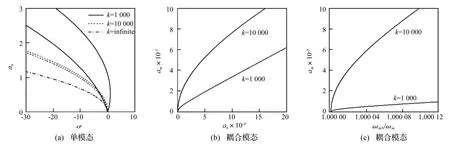
图5 b=b1时非线性模态的幅值与频率Fig.5.Amplitude and frequency of nonlinear normalmode at b=b1

3.3 非线性模态的时空效应

为了进一步对非线性模态进行数值描述，图6绘出了k取1 000、10 000和→∞三种情况下浅拱在一个周期内的形状变化示意图，其中细虚线表示初始拱轴线，b=b1，cosγ=－1，T表示周期，从中可以看到弹性约束端的竖向位移随时间波动。图7则给出了不同k值下跨中、弹性约束端两个位置竖向位移的时间历程曲线。通过对比可发现:k越大，跨中竖向位移越大(图7(a));弹性约束端竖向位移越小(图7(b))，且k→∞为零。

图6 弹性约束浅拱一个周期内的形状变化Fig.6 Variation over a period of the dynamic configurations for elastically constrained shallow arch

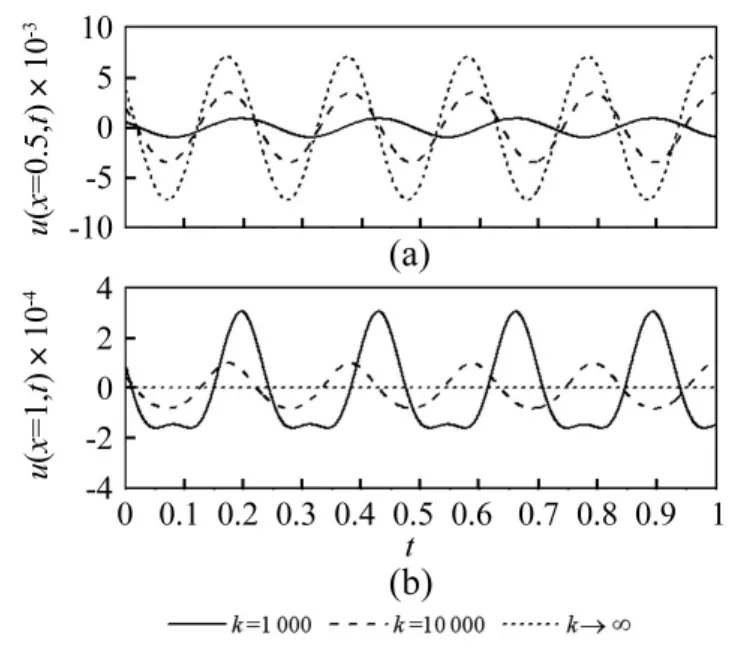
图7 跨中、弹性约束端时间历程图Fig.7 Time history of deflection atmiddle point and elastically constrained end

4 结论

文中采用多尺度直接摄动法构造了一端竖向弹性约束浅拱发生2∶1内共振时的非线性模态，以最低两阶模态之间的2∶1内共振为研究对象，探讨了竖向约束刚度值对线性模态、形函数、内共振激发条件及非线性模态时空效应等的影响。

(1)弹性约束导致线性模态、形函数不对称且约束端出现非零值;

(2)弹性约束使得最低两阶模态之间的2∶1内共振被激发，相同条件下固支浅拱未被激发;

(3)不同竖向约束刚度k值下，非线性模态的时空效应呈现不同的动力形态。

［1］Zhou L Q，Chen Y S，Chen FQ.Global bifurcation analysis and chaos of an arch structure with parametric and forced excitation［J］.Mechanics Research Communications，2010，37(1):67－71.

［2］王钟羡，江波，孙保昌.周期激励浅拱的全局分岔［J］.浙江大学学报:自然科学版，2004，25(1):85－88.

WANG Zhong－xian，JIANG Bo，SUN Bao－chang.Global bifurcation of shallow arch with periodic excitation［J］.Journal of Jiangsu University:Natural Science Edition，2004，25(1):85－88.

［3］Malhotra N，Namachchivaya N S.Chaotic dynamic of shallow arch structures under 1∶2 resonance;Chaotic motion of shallow arch structures under 1∶1 internal resonance［J］.Journal Engineering Mechanics，1997，123(6):612－627.

［4］Xu JX，Huang H，Zhang P Z，et al.Dynamic stability of shallow arch with elastic supports－application in the dynamic stability analysis of inner winding of transformer during short circuit［J］.International Journal of Non－Linear Mechanics，2002，37(4/5):909－920.

［5］Lacarbonara W，Arafat H N，Nayfeh A H.Non－linear interactions in imperfect beams at veering［J］.International Journal of Non－Linear Mechanics，2005，40(7):987－1003.

［6］康婷，白应生，孙惠香.水平弹性支撑圆拱的动力特性研究［J］.力学与实践，2013，35(2):50－55.

KANG Ting，BAI Ying－sheng，SUN Hui－xiang.Dynamic characteristics of the horizontal elastic support circular arch［J］.Mechanics in Engineering，2013，35(2):50－55.

［7］Rosenberg R M.The normalmodes of nonlinear n－degree－offreedom systems［J］，Journal of Applied Mechanics，1962，29(1):7－14.

［8］Shaw SW，Peirre C.Nonlinear normalmodes and invariant manifolds［J］.Journal of Sound and Vibration，1991，150 (1):170－173.

［9］Nayfeh A H，Mook D T.Nonlinear Oscillations［M］.New York:John Wiley＆Sons Inc，1979.

［10］Vakakis A F.Nonsimilar normal oscillations in a strongly nonlinear discrete system［J］.Journal of Sound and Vibration，1992，158(2):341－361.

［11］陈予恕，吴志强.非线性模态理论的研究进展［J］.力学进展，1997，27(3):289－300.

CHEN Yu－shu，WU Zhi－qiang.Advances in study on theories of nonlinear normal modes［J］.Advances in Mechanics，1997，27(3):289－300.

［12］Nayfeh A H，Lacarbonara W，Chin C M.Nonlinear normal modes ofbuckled beams:three－to－one and one－to－one internal resonances［J］.Nonlinear Dynamics，1999，18(3):253－273.

［13］Li X Y，Chen Y S，Wu Z Q.Non－linear normalmodes and their bifurcation of a class of systems with three double of pure imaginary roots and dual internal resonances［J］.International Journal of Non－Linear Mechanics，2004，39(2): 189－199.

［14］Mamandi A，Kargarnovin M H，Farsi S.Dynamic analysis of a simply supported beam resting on a nonlinear elastic foundation under compressive axial load using nonlinear normal modes techniques under three－to－one internal resonance condition［J］.Nonlinear Dynamics，2012，70(2): 1147－1172.

［15］Lacarbonara W，Rega G，Nayfeh A H.Resonant non－linear normalmodes.Part I:analytical treatment for structural onedimenensional systems［J］.International Journal of Nonlinear Mechanics.2003，38(6):851－872.

［16］LacarbonaraW，Rega G.Resonantnon－linear normalmodes.Part II:activation orthogonality conditions for shallow structural systems［J］.International Journal of Non－linear Mechanics.2003，38(6):873－887.

Nonlinear normalmodes associated w ith internal resonance for an elastically constrained shallow arch

ZENG You－yi，YIZhuang－peng
(School of Civil Engineering and Architecture，Changsha University of Science and Technology，Changsha 410114，China)

When a dynamic system is elastically constrained，its natural vibration features and nonlinear normal modes are different from those under ideal boundary conditions.The constrain stiffness values change parametric regions of various nonlinear dynamic behaviors.The nonlinear normalmodes of a shallow arch with one end elastically constrained along vertical direction in a case of2∶1 internal resonancewere constructed by using themulti－scalemethod and the direct perturbation here.The research results showed that an internal resonant nonlinear system has both a singled－modemotion and coupled－mode motions;the existence and various values of elastic constraint lead to different asymmetric linear modes，shape functions and internal resonance exciting conditions;moreover，the space－time effects of nonlinear normal modeswith different constraint stiffnesses display different dynamic configurations.

elastically constrained;shallow arch;nonlinear normal modes;2:1 internal resonance;multiscalemethod

U311.2

A

10.13465/j.cnki.jvs.2015.23.009

国家自然科学基金资助项目(11002030);长沙理工大学土木工程重点学科基金项目(15ZDXK01)

2014－07－21修改稿收到日期:2014－12－04

曾有艺男，硕士，讲师，博士生，1979年生

易壮鹏男，博士，副教授，硕士生导师，1979年生邮箱:yizhuangpeng@163.com