一种改进Mathieu方程动力不稳定边界的方法

王杰方，安伟光，宋向华

（哈尔滨工程大学航天工程系，哈尔滨 150001）

一种改进Mathieu方程动力不稳定边界的方法

王杰方，安伟光，宋向华

（哈尔滨工程大学航天工程系，哈尔滨 150001）

基于Mathieu方程的临界频率方程式，提出了一种改进Mathieu方程不稳定边界的方法，并获得了比Bolotin近似边界更精确的前三阶收敛的不稳定边界。从改进的不稳定区域边界表达式和Bolotin近似公式的对比中发现：两种方法获得的第一、二阶不稳定区域相差不大，但相较于Bolotin的第三阶不稳定区域，改进的第三阶不稳定区域整体上移，且上移幅度随着激发系数的增大而增大。当激发系数μ取0．5时，上边界上移幅度为8．61%，下边界上移幅度为11．56%。对于受低频载荷作用的动力稳定性问题，第三阶不稳定边界公式的改进具有重要的意义。

动力稳定性；Mathieu方程；临界频率；动力不稳定区域

Mathieu方程式常见于物理和工程的各个领域中：赵晶瑞［1］对一种新型的深海顺应式采油平台（Spar平台）的纵摇运动进行了分析，得到了具有三次非线性项的有阻尼Mathieu方程。另外，在载流薄板的磁弹性动力屈曲问题中也存在Mathieu方程［2］。Li等［3］利用Mathieu方程分析了谐振式惯性传感器的动力学特性。Mathieu方程有一个最重要的性质：当它们的系数间存在某种关系时，方程式具有无限增长的解，这些解在对应的参数平面上完全布满了许多区域，这些区域相当于不稳定区域［4］。因此，确定不稳定区域是研究Mathieu方程问题的重点。

现有文献中关于不稳定区域的分析方法主要有摄动法和傅里叶分析法［5］：摄动法［6］适用于小参数的情况，傅里叶分析法［7－8］适用于大参数的情况，例如，在实际的海洋环境下，Mathieu方程中的参数不再是小参数［5，9］，摄动法不再适用，需要采用傅里叶分析法。由于不稳定区在任何工程或者物理问题中都属于必须避开的禁区，因此其精确性是十分重要的。文中将对目前广泛采用的傅里叶分析法进行改进，推导出比文献［4］中的Bolotin近似公式更精确的不稳定边界公式。

本文思路是：将周期解按傅里叶级数展开并代入Mathieu方程中得到临界频率方程式，依次从临界频率方程式中提取n阶前主子行列式等式，然后将其转化为一元n次方程（n≤4），通过多次直接求解一元n次方程的根来获得收敛的不稳定边界表达式。

1 结构动力稳定性问题

1.1 结构动力稳定性问题的Mathieu方程

以简谐纵向力P＝P0（1+βcos（θt））作用下的铰支直杆的动力稳定性问题为例［4］，其Mathieu方程为

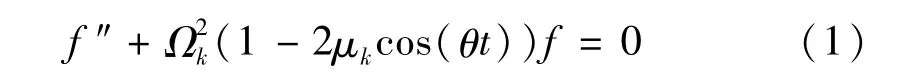
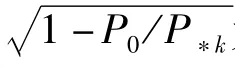
从静力屈曲角度：纵向力的最大值Pmax＝（1+ β）P0须小于临界屈曲载荷p*1，即P0须小于P*1／（1+ β）。假设P0＝P*1／（1+β），代入μk中得，β取任意值时，激发系数μ恒等于0．5。由于μk是随P0单调递增的函数，所以激发系数μk的取值范围为（0，0．5）。

Mathieu方程存在周期为T和2T的周期解，且周期相同的两个解包围着不稳定区，周期不同的两个解包围着稳定区。因此，找出使Mathieu方程具有周期T和2T的周期解的条件就可以确定不稳定边界［4］。

1.2 与周期为2T的周期解对应的临界频率方程式

将Mathieu方程的解展开为

并代入Mathieu方程中，得到与周期2T的周期解对应的临界频率方程式为

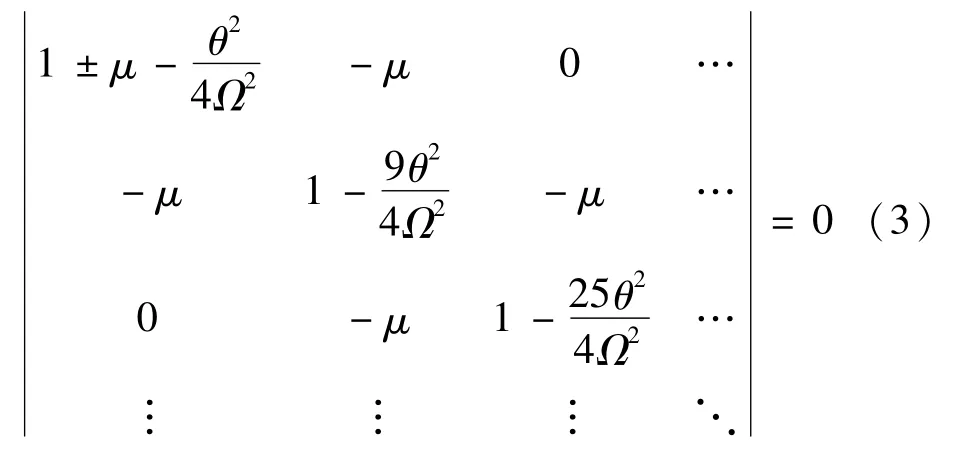
周期2T的周期解包围的不稳定区域由式（3）确定。

1.3 与周期为T的周期解对应的临界频率方程式

同样，将Mathieu方程的解展开为

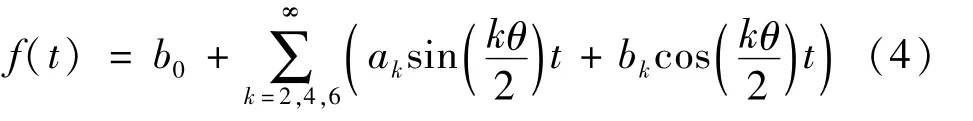
得到与周期T的周期解对应的临界频率方程式

周期T的周期解包围的不稳定区由式（5），式（6）确定。

2 改进Mathieu方程不稳定边界的方法

2．1 与周期2T的周期解对应的动力不稳定区域边界

（1）若式（2）中的系数a1，b1存在非零解，其他系数为0，对应于式（3）的左上角的对角线元素为0，从而获得第一阶动力不稳定区域的边界表达式

式中：u表示上边界，d表示下边界，θ*iju表示第j次计算的第i阶上边界，j表示第j次计算的不稳定边界，下同。上式中的第一阶动力不稳定区域边界表达式是关于Mathieu方程存在周期为2T的周期解严格成立的条件，但它们并不是完整的第一阶不稳定区域的边界。下面将会对第一阶不稳定区域的边界表达式进行进一步的推导计算和修正，以获得完整的、收敛的第一阶不稳定区域边界。

（2）若式（2）中的系数a1，b1，a3，b3存在非零解，其他系数为0，对应于式（3）中2阶前主子行列式等于0，得到第二个第一阶动力不稳定区域的边界

图1 第一次修正后的第一阶不稳定区域Fig．1 The first order unstable region after the first amend

从图1可知，上边界θ*12u在 θ*11u之上，下边界θ*12d包含在θ*11d之内，所以经第一修正后的第一阶不稳定区域的边界为 (θ*12u，θ*11d)。

（3）若式（2）中的系数a1，a3，a5和b1，b3，b5，存在非零解，其他系数为0，对应于式（3）中3阶前主子行列式等于0，将它们化为两个标准的一元三次方程，

式中：x1＝x2＝θ2／4Ω2。

采用盛金公式求解上述两个一元三次方程的根，即可获得不稳定区域的边界公式。盛金判别式为

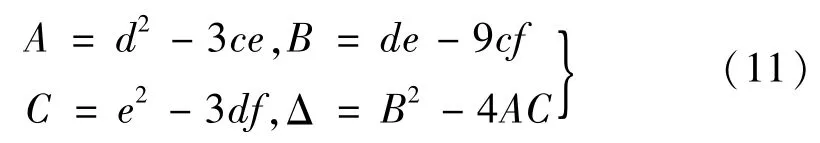
第三个第一阶动力不稳定区域的边界为

图2给出了将不稳定区（θ*32u，θ*32d）与（θ*31u，θ*31d）整合后得到的第一次修正的第三阶动力不稳定区域。

图2 第一修正后的第三阶不稳定区域Fig．2 The third order unstable region after the first amend

从图2可知，第三阶不稳定区域的上边界θ*32u在θ*31u之上，下边界θ*32d包含在下边界θ*31d之内，所以，经第一次修正后的第三阶不稳定区域的边界为（θ*32u， θ*31d）。另外，经计算发现θ*13u和θ*13d的值与上文中的θ*12u和θ*12d非常相近，这说明第一次修正后得到的边界（θ*12u，θ*11d）是已经收敛的边界，因此并不需要对第一阶不稳定区进行第二次修正。收敛的第一阶不稳定区域的边界表达式为

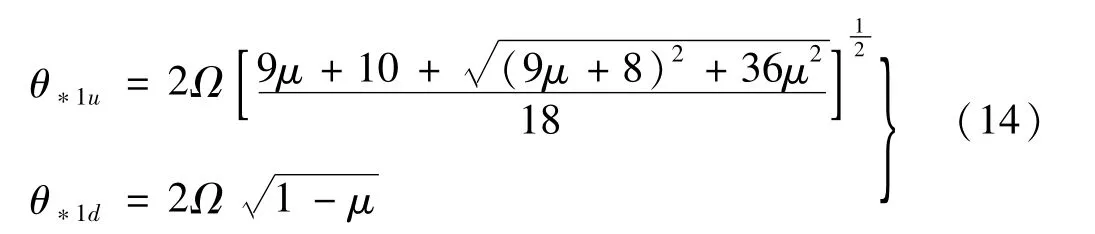
（4）若式（2）中的系数a1，a3，a5，a7和b1，b3，b5，b7存在非零解，其他系数为0，即式（3）中4阶前主子行列式等于0，将这两个4阶行列式等式化为标准的一元四次方程，

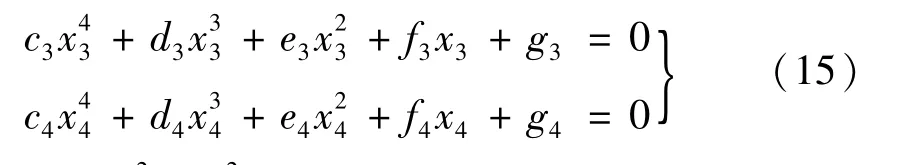
式中：x3＝x4＝θ2／4Ω2。

采用置换群解法求解上述两个一元四次方程的根即可获得不稳定区边界。置换群法的相关判别式为

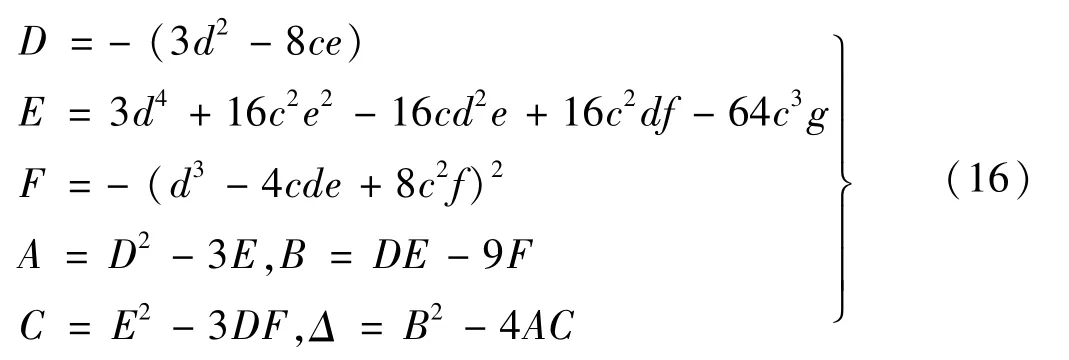
第三个第三阶动力不稳定区域的边界

当μ∈［0，0．5］时，θ*14u和θ*14d的值与上文中的θ*13u和θ*13d几乎一致，这也再一次验证了式（14）是收敛的。当μ∈［0，0．5］时，θ*33u的值略高于θ*32u（激发系数取0．5时，变化幅度仅为0．3%），因此第三阶动力不稳定区域的边界仍为（θ*32u，θ*31d）。最终得到收敛的第三阶动力不稳定区域的上下边界表达式为

2．2 与周期T的周期解对应的动力不稳定区域边界

（1）式（5）的左上角的对角线元素为0，式（6）中2阶前主子行列式为0，得

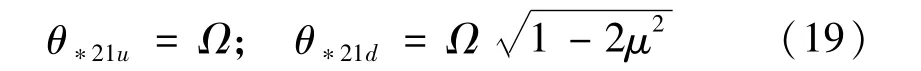
（2）式（5）中的2阶前主子行列式为0，式（6）中

3阶前主子行列式为0，得到第二个第二阶动力不稳定区域的边界

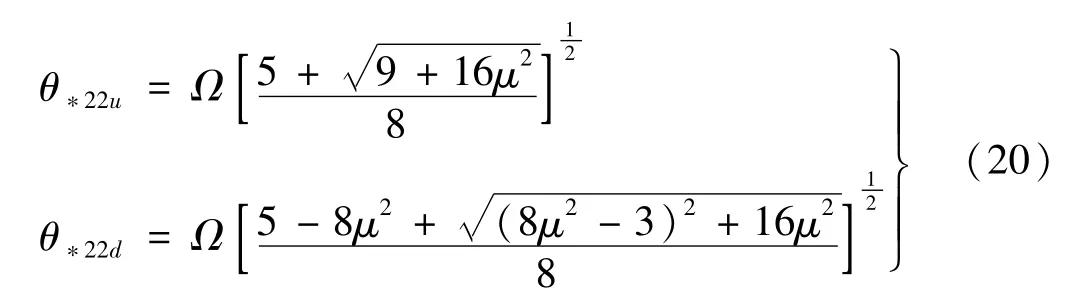
将（θ*22u，θ*22d）与（θ*21u，θ*21d）整合起来得到第一次修正后的第二阶动力不稳定区域见图3。

图3 第一次修正后的第二阶不稳定区域Fig．3 The second order unstable region after the first amend

从图3可知，第二阶不稳定区域的上边界θ*22u在θ*21u之上，下边界θ*22d包含在下边界θ*21d之内，所以经第一修正后的第二阶不稳定区域的边界为（θ*22u，θ*21d）。

（3）式（5）中的3阶前主子行列式为0，式（6）中4阶前主子行列式为0，获得两个标准的一元三次方程，

式中：x5＝x6＝θ2／Ω2。

采用盛金公式求解上述方程的根，能够获得第三个第二阶动力不稳定区域的边界

式中：θi，Ai的含义与式（12）和式（13）相同。

计算表明，当μ∈［0，0．5］时，θ*23u和θ*23d的所夹的不稳定区域被（θ*22u，θ*21d）包裹，因此不需要对第二阶动力不稳定区边界进行第二次修正。最终得到收敛的第二阶动力不稳定区域的上下边界表达式是

（4）式（5）中的4阶前主子行列式为0，式（6）中5阶前主子行列式为0，获得两个标准的一元四次方程，

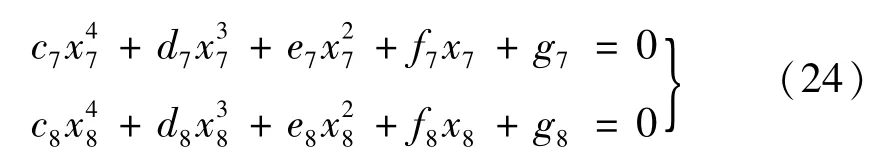
式中：x7＝x8＝θ2／Ω2。

采用置换群法求解上述方程的根，即可获得第四个第二阶动力不稳定区域的边界

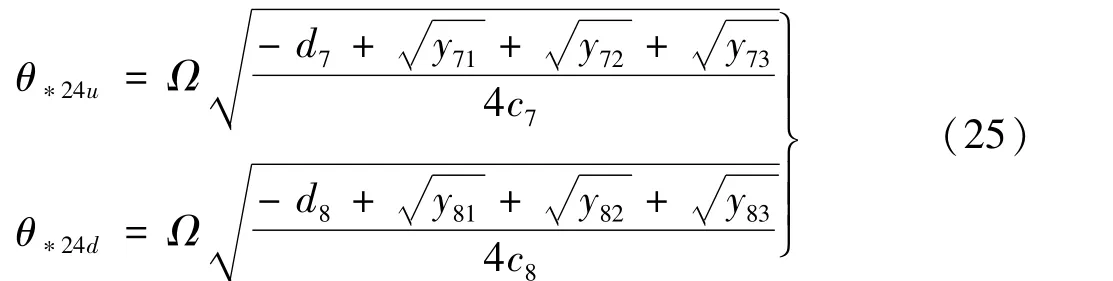
式中：yi1，yi2，yi3，θi的含义与式（17）中相同。

计算表明，在μ∈[0，0．]5范围内，θ*24u和θ*24d的值与上文中的θ*23u和θ*23d几乎一致，这也再一次验证了式（23）的收敛性。

3 改进的不稳定边界与Bolotin近似边界比较

为了获得收敛的前三阶不稳定边界，需要从临界频率方程式中提取的最高次方程为一元四次方程。经验算，文中采用盛金公式求解一元三次方程的根和采用置换群法求解一元四次方程的根时，其误差的数量级仅为10－15，完全可以认为每一步的求解过程并不产生误差。不稳定边界的误差只与最终收敛情况有关，但边界的收敛却是可控的。文中的前三阶不稳定边界（式（14）、式（23）和式（18））经过多次修正已是收敛的边界，因此采用本方法能获得比Bolotin近似边界更精确的表达式。

3.1 改进的不稳定边界与Bolotin近似边界的比较

将改进的前三阶不稳定区域边界表达式（14）、式（23）和式（18）与Bolotin前三阶不稳定区域近似边界公式［4］进行对比。图4～图6中分别给出了第一阶、第二阶、第三阶改进的不稳定边界和Bolotin近似边界的曲线图，实线表示改进的不稳定边界，虚线表示Bolotin近似边界。注意，由于本改进的第一阶和第二阶不稳定区域的下边界表达式与Bolotin方法给出的边界公式相同，因此，图4和图5中的下边界只有一条实曲线。

图4 第一阶不稳定区域的比较Fig．4 Comparison of the first order dynamic unstable region

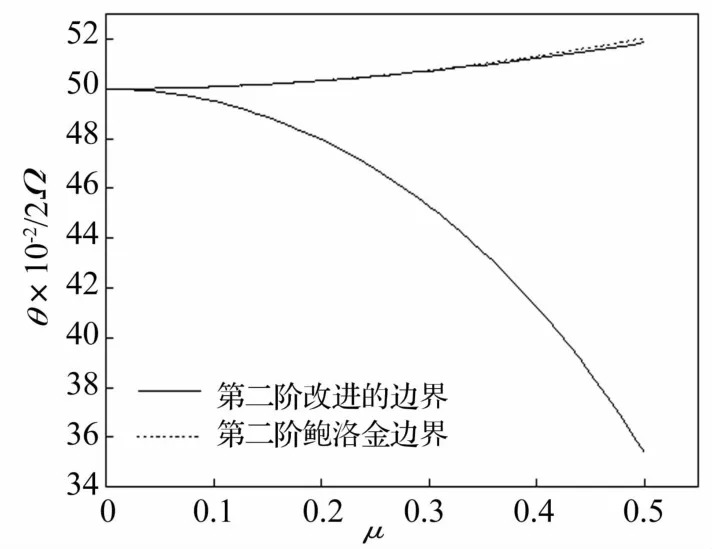
图5 第二阶不稳定区域的比较Fig．5 Comparison of the second order dynamic unstable region

图6 第三阶不稳定区域的比较Fig．6 Comparison of the third order dynamic unstable region

从图4和图5中可知，对于第一阶、第二阶不稳定区域的上边界，两种计算方法得出的结果相差都不大。计算表明，当μ＝0．5时，两种方法计算的第一阶上边界误差仅为0．653%，第二阶上边界误差也仅为－0．193%。这说明采用本方法获得的第一阶和第二阶不稳定区边界表达式的精确度是合理的。

从图6可知，相较于第三阶Bolotin不稳定区域，改进的第三阶不稳定区域整体上移，且上移幅度随着激发系数的增大而增大。当μ分别取0．1、0．2、0．3、0．4、0．5时，改进的第三阶不稳定区域的上边界较Bolotin的第三阶上边界的上移幅度分别为1．003%、1．223%、2．492%、5．128%、8．609%；当μ分别取0．1、0．2、0．3、0．4、0．5时，改进第三阶不稳定区域的下边界的上移幅度分别为0．0%、0．0%、0．326%、1．832%、11．558%，偏差较大，不能忽略。

3.2 第三阶动力不稳定区域边界改进的意义

以文献［10］中的水下超空泡高速航行器为例：超空泡尾部脉动和尾涡脱落产生的空泡高频特征频率θ的取值范围为80～160 Hz，航行器壳体的特征频率ω＝149 Hz，分析航行器的动力不稳定区域与外载荷频率之间的位置关系。

对于水下高速航行器的动力屈曲问题而言，其第一阶不稳定区域位于2Ω附近，第二阶不稳定区域位于Ω附近，第三阶不稳定区域位于2Ω／3附近，用定值分量P0和临界力P*表示为

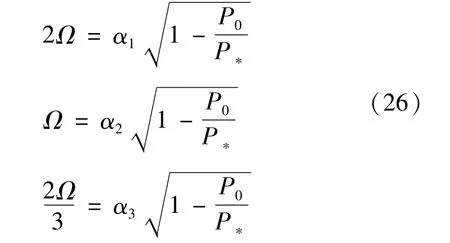
其中，临界力只与结构参数有关，与周期力无关。α1，α2，α3依次为第一阶、第二阶、第三阶不稳定区域边界的系数，且α1＝298，α2＝149，α3＝99．3。下面的第一阶、第二阶、第三阶不稳定区域上下边界的系数依次用（α1u，α1d）、（α2u，α2d）、（α3u，α3d）来表示。由于μ＝0时，不稳定区域的上下边界相等，所以上式的系数省略了下角标u和d。

表1给出了激发系数μ取不同值时，改进的前三阶不稳定区域上下边界系数（α1u，α1d），（α2u，α2d），（α3u，α3d）的值和第三阶Bolotin不稳定边界系数（α3u′，α3d′）。

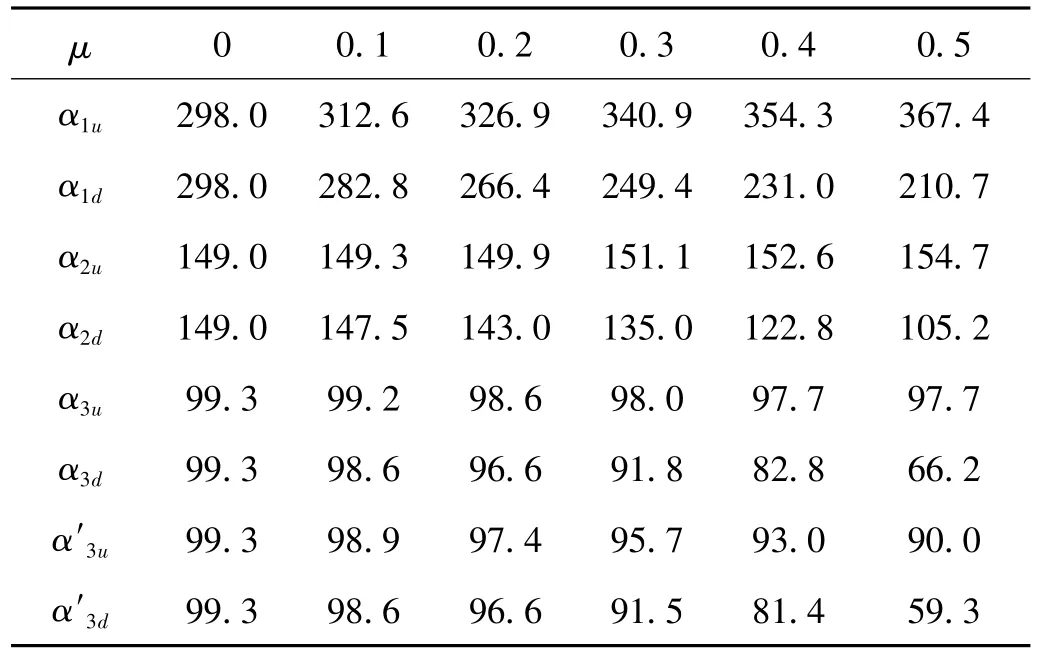
表1 前三阶不稳定区域边界的系数Tab.1 The coefficient of the first three order unstable region

以μ＝0．5时的不稳定区为例，结合表1中的数据，经计算发现：

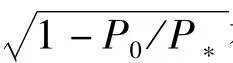
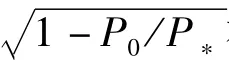
从以上四个结论可知：① 当P0／P*的值较大时，第一二阶不稳定区与载荷频率发生重合的可能性较大，是主要的不稳定区。② 当P0／P*的值较小时，第三阶不稳定区域与外载荷频率区间发生重合的可能性较大，也可能是主要的不稳定区域。且从“（3）”和“（4）”的对比中可知：采用改进的不稳定边界表达式，P0／P*＞0．33时才能避开第三阶不稳定区域，而采用Bolotin的近似边界表达式时，P0／P*＞0．21时就能避开第三阶不稳定区域。也就是说，采用Bolotin的近似边界表达式认为(0．21，0．33)是P0／P*的安全取值范围，但采用改进的第三阶不稳定表达式认为(0．21，0．33)是P0／P*的危险取值范围。这说明采用精度更高的改进不稳定边界使结构避免了采用Bolotin近似公式时所隐藏的危险。

4 超空泡运动体圆柱薄壳舱段的动力稳定性分析算例

超空泡运动体航行深度H＝10 m，流场密度ρw＝1 000 kg／m3，对于自然超空泡，空泡内的饱和蒸汽压pc＝2 350 Pa（20°C），标准大气压p＝101 325 Pa。圆柱薄壳舱段的几何参数：半径R＝0．2 m，长度L＝4 m，厚度h＝3 mm，空化器直径dn＝0．2 m。材料物理参数：弹性模量E＝209 GPa，材料密度ρ＝7 850 kg／m3，泊松比ν＝0．3。

基于文献［11］中圆柱薄壳动力稳定性微分方程，采用Bolotin方法和本方法计算超空泡运动体圆柱舱段的动力不稳定区。图7～图9给出了i＝1，k＝1（i，k分别为轴向和周向的半波数）时，依赖于航行速度V（m／s）和频率f／Hz的前三阶动力不稳定区域。

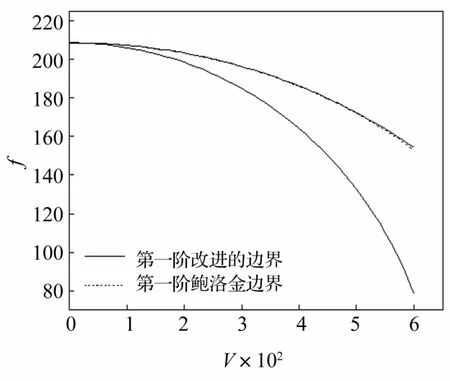
图7 第一阶不稳定区域的比较Fig．7 Comparison of the first order dynamic unstable region

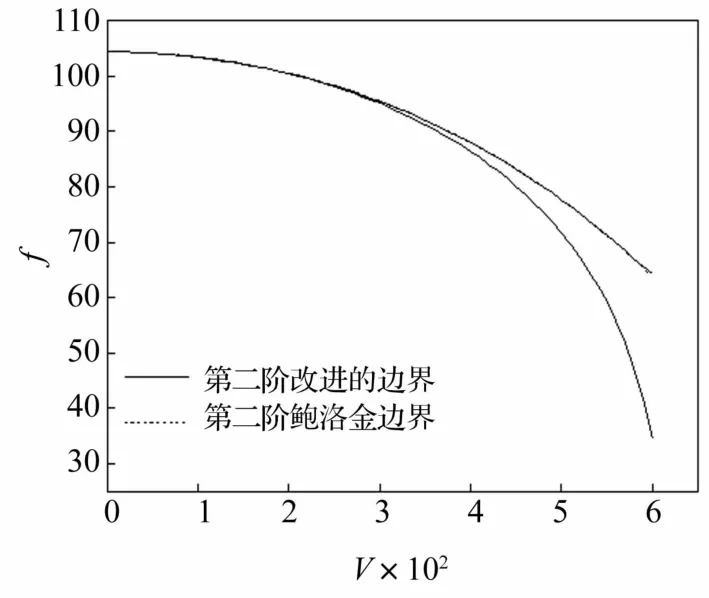
图8 第二阶不稳定区域的比较Fig．8 Comparison of the second order dynamic unstable region

图9 第三阶不稳定区域的比较Fig．9 Comparison of the third order dynamic unstable region

从图7～图9可知，随着航行速度的增大，超空泡运动体圆柱薄壳舱段的不稳定区间宽度也在不断地增大。由图7和图8可知，对于第一阶和第二阶不稳定区域，采用Bolotin方法和本方法获得的结果相差甚小，可以忽略；但是，从图9可知，采用本文方法获得的不稳定区较Bolotin方法获得的不稳定区整体上移，且航行速度越大上移幅度越大，这一结论与3．1节中的结论是一致的。

5 结 论

本文是采用多次直接求解一元n次方程的根来获得不稳定边界表达式的。首先，利用盛金公式求解一元三次方程的根和置换群法求解一元四次方程的根时，其误差的数量级仅为10－15，完全可以认为每一步的求解并不产生误差；其次，文中的前三阶不稳定边界经过多次修正已是收敛的边界。以上两点确保了本文改进方法的精确度。并得出以下结论：

（1）从改进的不稳定区域边界表达式和Bolotin近似公式的对比中发现：两种方法获得的第一阶、第二阶动力不稳定区域相差不大；相较于第三阶Bolotin不稳定区域，本文方法获得的改进的第三阶不稳定区域整体上移，且上移幅度随着激发系数的增大而增大，当μ＝0．5时，上边界上移幅度为8．61%，下边界上移幅度为11．56%。

（2）从水下超空泡高速航行器的动力稳定性分析算例中可知：当P0／P*的值较小时，第三阶不稳定区域与外载荷频率区间发生重合的可能性较大，也可能是主要的不稳定区域。

（3）采用精度更高的改进的不稳定边界使结构避免了采用Bolotin不稳定近似公式时所隐藏的危险。

综上所述，由改进的傅里叶分析法确定的不稳定区边界的精度，为Mathieu方程的动力不稳定区提供了比Bolotin不稳定区域更精确的边界表达式。

［1］赵晶瑞，唐友刚，王文杰．传统Spar平台参数激励Mathieu不稳定性的研究［J］．工程力学，2010，27（3）：222－227．

ZHAO Jing-rui，TANG You-gang，WANGWen-jie．Study on the parametrically excited mathieu instability of a classic spar platform［J］．Engineering Mechanics，2010，27（3）：222－227．

［2］王平，王知人，白象忠．马丢方程解的稳定性在磁弹性屈曲中的应用［J］．哈尔滨工业大学学报，2009，41（11）：222－224．

WANG Ping，WANG Zhi-ren，BAI Xiang-zhong．Applications of the stability of Mathieu equation's solution in magnetic-elastisity buckling problem［J］．Journal of Harbin Institute of Technology，2009，41（11）：222－224．

［3］Li Yan，Fan Shang-chun，Guo Zhan-she．Mathieu equation with application to analysis of dynamic characteristics of resonant inertial sensors［J］．Commun Nonlinear Sci Numer Simulat，2013，18：401－410．

［4］Bolotin，V V．The Dynamic Stability of Elstic Systems［M］．Holen-Day San Francisco，1964．

［5］徐万海，吴应湘，钟兴福，等．海洋细长结构参数激励不稳定区的确定方法［J］．振动与冲击，2011，30（9）：79－83．

XU Wan-hai，WU Ying-xiang，ZHONG Xing-fu，et al．Methods for parametric excitation instability analysis of slender flexible cylindrical structures in offshore engineering［J］．Journal of Vibration and Shock，2011，30（9）：79－83．

［6］Nayfeh A H．Introduction to Perturbation Technique［M］．New York：Wiley，1981．

［7］冯世宁，陈浩然．含分层损伤复合材料层合板非线性动力稳定性［J］．复合材料学报，2006，23（1）：154－160．

FENG Shi-ning，CHEN Hao-ran．Nonlinear dynamic instability behavior of delaminated composite laminates［J］．Acta Materiae Compositae Sinica，2006，23（1）：154－160．

［8］赵洪金，董宁娟，刘超，等．基于能量法的高温（火灾）环境下轴心受压格构柱动力稳定性分析［J］．工 程 力 学，2011，28（12）：160－165．

ZHAO Hong-jin，DONG Ning-juan，LIU Chao，et al．Dynamic stability analysis on axial compression lattice column under high temperature condition using energy method［J］．Engineering Mechanics，2011，28（12）：160－165．

［9］王俊荣，谢彬．深水半潜式平台Mathieu不稳定问题研究［J］．工程力学，2012，29（10）：347－353．

WANG Jun-rong，XIE Bin．Mathieu instablity study of a deepwater semi-submersible platform［J］．Engineering Mechanics，2012，29（10）：347－353．

［10］党建军，张谋，郭芳，等．超空泡脉动对水下高速航行器壳体强度的影响研究［J］．机械科学与技术，2011，30（11）：1930－1933．

DANG Jian-jun，ZHANG Mou，GUO Fang，et al．A study of the influence of the super-cavit pulsation on the intensity of the shell of the high-speed underwater vehicle［J］．Mechanical Science and Technology for Aerospace Engineering，2011，30（11）：1930－1933．

［11］王杰方，安伟光，宋向华．超空泡运动体圆柱薄壳动力屈曲及可靠性分析［J］．振动与冲击，2014，33（8）：22－28．

WANG Jie-fang，AN Wei-guang，SONG Xiang-hua．Dynamic buckling and reliability analysis of a cylindrical thin shell for supercavitating vehicles［J］．Journal of Vibration and Shock，2014，33（8）：22－28．

Im proved method about dynam ic unstable boundary ofmathieu equation

WANG Jie-fang，ANWei-guang，SONG Xiang-hua
（Department of Aerospace Engineering，Harbin Engineering University，Harbin 150001，China）

An improvedmethod about unstable boundary of Mathieu equation was proposed according to the critical frequency equation，and the first three orders convergent unstable boundary was got，which ismore accurate than the Bolotin approximate boundary．Comparing the twomethods，it shows that their first two orders dynamic unstable region are almost the same，the third order unstable region of the improved method moves upward compared with the Bolotinmethod，and the range is amplified with the growth of excitation coefficient．When the excitation coefficientμis 0．5，the upper boundarymoves upward about8．61%and the lower boundary moves upward about 11．56%．With respect the dynamic stability problem caused by low frequency loading，the improvement on the third order unstable boundary expression has great significance．

dynamic stability；mathieu equation；critical frequency；dynamic unstable region

O342

A

10．13465／j．cnki．jvs．2015．12．031

国家科技部国际合作专项（2012DFR00070）

2014－04－28 修改稿收到日期：2014－05－27第一作者王杰方女，博士，1987年生

安伟光 男，教授，博士生导师，1943年生

邮箱：anweiguang＠hrbeu．edu．cn