高斯数论研究刍议及其生平补遗——纪念高斯逝世160周年

金亚南，徐沥泉

①无锡旅游商贸高等职业技术学校，江苏 无锡 214045；②无锡市教育科学研究院，江苏 无锡 214001

高斯数论研究刍议及其生平补遗
——纪念高斯逝世160周年

金亚南①，徐沥泉②†

①无锡旅游商贸高等职业技术学校，江苏 无锡 214045；②无锡市教育科学研究院，江苏 无锡 214001

高斯是继欧拉与拉格郎日之后把分析方法应用于数论研究的又一位数学大师。本文扼要地综述高斯数论研究的早期工作，其中有许多激动人心的数论公式与定理。例如：正十七边形的解，高斯和，二次互反律的证明；高斯的名著《算术研究》中较多的篇幅都涉及到了二次同余和二次型、代数学基本定理，高斯整数环的概念等，以及高斯在解决这些问题的同时所创造的证明方法和概念。这些概念、定理或公式都是高斯发明并加以精确论证的。与众不同的是，他善于把复杂问题变换为一个简单问题。事实上，高斯的想法更具一般性，并足以展示高斯数学工作的深刻性。文中的某些典型例子反映了他深刻的洞察力。从高斯对数学科学的发现和发明中，我们还可以领略与欣赏到他深邃的创造性思维活动中的方法论价值。他并没有把他的发现和发明过程掩盖起来，而是记载在他的工作日记和给友人的信件之中。

算术研究；正十七边形；二次互反律；高斯和；高斯整数环

如果说费马是现代数论研究的先驱，那么毫无疑问，高斯则是现代数论研究的奠基者。卡尔•弗里德里希•高斯(Carl Friedrich Gauss)生于1777年，卒于1855年，逝世已160周年。他是众所周知的那个时代最伟大的数学家。他在数论方面的主要著作有《算术研究》(中国台湾学者把它译作《整数论研考》)。数论在数学中的地位是独特的，对此高斯曾经说过：“数学是科学的皇后，数论是数学中的皇冠。”高斯的名著《算术研究》于1801年问世，由此开创了数论研究的全新方式，是数论研究系统化、科学化的划时代著作。除此之外，高斯还有若干数论方面的小论文，其中包括许多深刻和专门的结果。当然，这里只能涉及其中的一小部分。

高斯的数学生涯经历了一条非凡而令人惊叹的道路，从他的工作日记中可见一斑。它告诉我们有关高斯的最重要的发现。高斯并不是人们所传言的那样，是一位隐匿其重大发现和研究过程的数学家，更不是有人形容的，高斯从不让人看到和发现他的研究过程与方法，就像一头在沙漠中行走的狡猾的狐狸，不时地用尾巴扫除掉自己所走过的足迹。不过高斯的一句座右铭“宁肯少些，但要好些”倒是真的，它恰如其分地刻画出了他一贯的研究风格。高斯对待学问十分严谨，他的研究成果不到自己认为已经是臻善致美、无懈可击时，他是不会发表出来的。

1 正十七边形作图、高斯二次互反律与高斯和

从文献[1]中我们可以了解到许多关于高斯的鲜为人知的思维方法与过程。1796年3月30日，他发现了五进制与二进制的割圆原理，即在几何上把圆17等分的可行性问题。尔后在他1819年写给Gerling的一封信中，高斯又进一步推广了他的关于正十七边形的可构造性原理(等分圆周原理以及用几何方法十七等分圆周)。他说：

“我联想到方程1+x+...+xp-1=0的所有的根，并对它们进行了集中的分析，依据算法的原理，我终于成功了！那是在布伦瑞克(Braunschweig)休假期间，那天早晨，在我起床之前，我清楚地看到了它们之间的这种联系，能够特殊地应用于正十七边形，并立刻用数值的方法一一验证了它们。”[1]64。

换言之，高斯解决了一个十分古老的古典问题——正十七边形的尺规作图问题，即正十七边形可以使用圆规和直尺作出。于是高斯首次发布了一个告示，并在这个告示中强调指出，他的方法足以彻底解决任何正n边形的作图问题，即：正n边形可以用圆规和直尺作出，当且仅当边数n=2kp1...pr,时。这里pi是费马素数，即形如22i+1的数。

仅几个星期后，1796年4月18日，高斯又第一个给出了关于二次互反律的完整证明：

这是他在几个月前独立于欧拉和勒让德(Legendre)所发现的。与之相联系，他发展了二元二次型的理论。他所建立的这一理论远远超越了他的前辈们，诸如拉格朗日(Lagrange)和勒让德的工作 。他的著名的《整数论研考》一书，于1801年在Latin这个地方首次出版。它所创建的理论为数论奠定了系统而坚实的基础，也极大地丰富了数学科学领域。在这之前，数论并没有成为数学的一个科学分支。用高斯的话来说，其中的最优美结果都是零星而杂乱无章地分布着，是靠人们的好运气被实验性地发现的，而对它们的证明“则深深地隐匿在黑暗之中，顽固地抵制所有的努力，挫败最锐利的探究”。数论中各种规律看起来互不相关、性质迥异，实际上却是紧密联系的。这些规律经常可以通过不同途径加以发现，殊途同归，最终加以比较之后找到一个最简单、最自然且令人满意的证明方法[2]。今天，关于如何构造正多边形作图的定理，已成为伽罗华(Galois)理论的一部分。一种数学理论越是向某些问题纵深发展之后，就常常会碰到更多令人惊奇的发现。

高斯在《整数论研考》(Disquisitiones Arithemeticae )第四节中把二次互反律称之为基本定理，居于一个突出的位置，因为它蕴含了所有二次剩余的理论。高斯着重指出了这个定理的重要性，它既可以判别二次同余式解的一般法则，同时也揭示了存在于质数对之间的一个意想不到的惊人的联系，一个支配质数的深刻的法则。高斯认为：“数论本质上分为两部分：同余理论和齐次式的理论。二项同余式理论是一般同余理论的核心组成部分，而互反律则是后一理论的基石。”

在高斯的一生中，给出这一基本定理八个不同的证明方法。他在与爱森斯坦(F. G. Eisenstein，1823—1852，高斯的学生，德国数学家)的对话中讲述自己在这方面的坎坷经历：“我在1795年独立地发现了这个定理，当时我对其他人在高等算术中的成就一无所知，因此并没有从相关文献上得到一星半点的帮助。这个定理折磨了我整整一年，付出了我最艰巨的努力，直到最后我终于得到了一个证明(作者注：1796年4月18日，他的第一种证法仅用到了整数性质，这是基本初等的方法)。后来我又发现了另外三个基于完全不同的原理的证明，其中有一个我已经在《整数论研考》的第五节中给出，其余的几个论优美都难以与之比肩，我保留着等将来发表。尽管这些证明在严格性上无可挑剔，它们的背景来源却都和原问题相去甚远。”[2]其中有几种证明方法，他用到了高斯和的理论。

“对根的符号的确定，使我们许多年来伤透了脑筋。在我所找到的一个问题的每一道关口都被蒙上了阴影。直到最后的四年里，碰巧有这么一个星期，由于不成功，我已经放弃了这样或者那样的企图，最后，也就是几天之前，我终于成功了。但是这一成功，与其说是作为我所寻找到的一个答案，倒不如说是由于上帝的恩赐而来，好像突然之间划出了一道闪光一样，它终于自己解开了这个谜。”[1]66

2 代数学基本定理和高斯数环

高斯对代数学的重要贡献是证明了代数学基本定理，他的存在性证明开创了数学研究的新途径。代数学基本定理是说，每个具有复系数的多项式都可以在复数域中被表示为若干个线性因子之积的形式。它有多种等价的表述，如每一个次数大于等于1的复系数多项式在复数域中有一根。利用复变函数论中的结论可以很简单地证明，这正是高斯所考虑的问题。高斯以其对该定理的高超证明，使数学界不仅对高斯本人而且对复数刮目相看，从而进一步确认了复数的地位。不仅如此，他又把复数带进了数论，并且创立了复整数理论。

高斯在该领域中最重要的成就是对三次和四次互反律的发现与证明。为此，他引进了高斯整数，即复整数。高斯证明了复整数在本质上具有和普通整数相同的性质，普通素数的许多定理可以转化为复素数的定理。更为重要的是，由高斯引入的复整数理论开辟了代数数论这一新的数论分支。这一理论，在19世纪得到了巨大的发展[3-5]。

这已经表明存在一种联系，即两数平方和的一种表达式。我们有||xy||=||x||·||y||。高斯证明了A是一个欧几里德(Euclidean)环。

众所周知，欧几里德算法(系统)准则的一条现存结果是A中的每一个元素都可以表为素元之积(所谓素元是指A中除本身及单位外无其他因子的元素)。整数中的非素数肯定不是素元，但并非素数都是A中的素元。例如：2=(-i)(1+i)2，(1+i)是一个素元。如果x是一个单位(可逆)元素，并且xy=1，可得||x||||y||=1，从而||x||=1，即x∈{1，-1，i，-i}。在此环中，可逆元素不再是±1，而是±1，±i。这方面高斯已经明确地认识到在A中分解素(数)因子的必要性。

在高斯整数环中定义了A中的ς函数：

展成“欧拉积”可得[6]

此公式中，ς(s)是Zeta函数，而L(s)称为L函数。

这里，

当s＞0时，L(s)收敛；而当s=1时恰恰就是莱伯尼兹级数：这正是我们所熟悉的。

让我们再一次考虑这个方程：

因为||x+iy||=x2+y2，

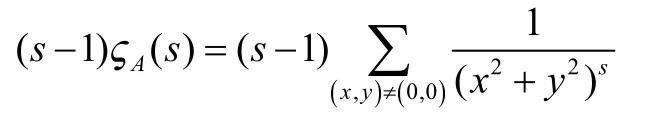
从直观上看，我们可以相当清楚地得到下面的一类近似等式(左边是一个关于积分的黎曼和)：

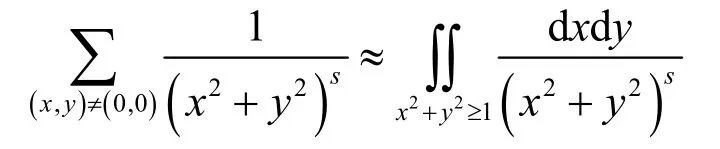
更精确地，我们有

计算此乘积是微积分中的一个标准练习题。我们代之以极坐标x=r cos φ，y=r sin φ，可得

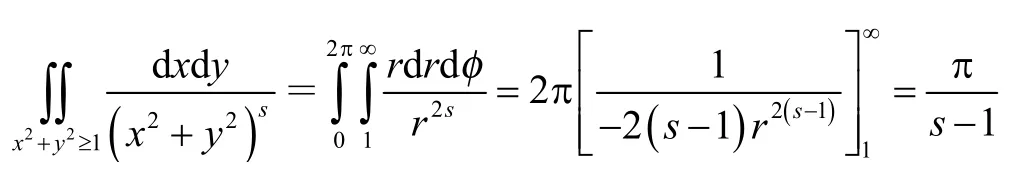
由此产生

最终又可得到莱伯尼兹级数：

令人意外的是，A中素因子的唯一分解问题竟与莱伯尼兹级数和p/4能联系到一起，但这个联系在数论中是极其重要的事实。它的一般原则被Dirichlet(迪里赫列德)完全发现。高斯对莱伯尼兹公式的证明非常简易，但是他从未发表过他的想法，尽管他还取得了另一些进展。这是当他完成《整数论研考》这部著作33年之后完成的，直到他去世之后才得以出版。至于在这方面，高斯本人是否给迪里赫列德提供过某种线索，能了解这一点是非常有趣的。令人遗憾的是，我们不得而知。迪里赫列德的论文中所涉及到这方面的成果也没有提供给高斯。高斯并没有对迪里赫列德的论文中的那些材料作过任何评论，迪里赫列德却发展了这些思想。总的说来，高斯对其他数学家的发现很少予以关注，但不关注迪里赫列德是非常可惜的，因为迪里赫列德是高斯可以从他那里获取这些思想的难得的数学家。

当然，高斯对现代数论研究的贡献远不止这些。尽管从费马、欧拉、拉格朗日、勒让德，直到敏可夫斯基等等，都出自数论本身的内在趣味及其所特有的美而进行过独自的研究，但高斯的工作是首先把先前人们所引用的符号标准化，运用二元二次型的语言非常彻底地完成了系列命题的公式化。他把已有的结果理论化和系统化，并开创了数学研究的新途径，奠定了近代数论的基础。

3 高斯生平补遗

最后，让我们使用少许篇幅总结一下高斯的人格与生平，其中有一些是鲜为人知的珍贵资料。欧拉的一位同事和远亲——Nicolaus Fuss，他以《L•欧拉的颂词》为例，从人们所期待的一种科学传记的需求，做出了如下的描述，这是1783年10月23日他在圣•彼得堡皇家科学院的一次会议上所作的演讲。他说：

“传记文学家要描述一位伟人的生平，都会从他所处的那个时代出发，赞扬伟人对开启人类智能所做出的贡献，并结合伟人高雅的风格进行生动的写照；另外，传记文学家本身也必须具备完备的科学知识，他所记述的内容应当是科学的最新进展。然而，在诸多基本素质之中，这两种素养对一些人来说并不是兼而有之的。尽管传记文学家们不需要使用那些不必要的装饰去修饰他的主题，但并不是说他不能从他的职责出发，自然地有鉴赏性地去组织素材，清楚地给予介绍，如实地进行记述。他应该揭示天才的伟人是如何产生的，应该调查周围环境怎样有助于杰出人才的造就与发展，对于伟人精湛的技艺给予广泛的解释，且这种赞扬不能忘记在天才人物出现之前对当时历史现状的分析，包括自然与社会。只有这样才能正确地定位和反映出真实水准。”

这里由于篇幅所限，我们不能对高斯的人品和贡献做出全面而系统的介绍。如果只需了解一个梗概的话，可阅读科学传记词典K. O. May的文章，和1977年德国布伦瑞克科协出版的迈尔-莱布尼茨的论著《Kreativitat》(创意)中关于高斯的论文[1]。W. K. Buhlerr的一本关于高斯的文学传记，则包含了更多的内容与信息，是一本新的非常杰出的传记。

高斯1777年4月30日出生于布伦瑞克。高斯的母亲婚前是女仆。他的父亲Gebhard Dietrich Gauss是个非常勤劳而严谨的人，从事过许多种工作，当过石匠、屠夫、园林工和泥瓦匠(water worker)。他总是日夜繁忙，试图改变其贫穷的家境。尔后，在1810年4月15日的一天，高斯对他的未婚妻Minna Waldeck这样描述过自己的父亲：

“我的父亲以他非常正直的人品和高雅的工作方式赢得了人们的尊敬，但是他在家里是一个非常独裁的人，粗暴而又急躁。我可以这样说，他在我幼小的心灵里已经失去了我对他的充分信任。即便这样也不会导致我们之间实际上的冲突，因为我早就变得非常地不依赖于他了。”

实际上，高斯在他那个朴素的家庭氛围中早就得到了某种锻炼，他那非凡的天资在早期就开始显露出来。他自己学会了怎样去阅读和计算。在小学里，高斯的老师——尤其是他的辅导老师(助教)Martin Bartels——已经发现了高斯在算术方面的天才。高斯9岁时，Bartels就开始给高斯特殊的训练，给他提供特别的教科书。这样一个突出的学生所产生的影响，引起了周围人们的关注。1877年，高斯违背了父亲的意愿进入大学预科学校读书，并由于学业进步巨大而得以跳级。在那儿他学习了两年。除了他在数学方面的聪明才智外，高斯在语言方面的天赋也是罕见的。1791年，正当高斯14岁那年，他在布伦瑞克Carl Wilhelm Ferdinand公爵的宫廷里，接受了公爵赠与他的一笔奖学金。这是从公爵私人的财务开支中拿出的数额有限的费用，但已足以使高斯在面临失学的关键时刻很容易地得以继续完成他正常的学业，直到30岁为止。

1792年，高斯进入布伦瑞克的Carolinum高等学校学习。在那里他阅读了大量的数学大师的著作，其中有牛顿的《自然哲学之数学原理》(Newton’s Principia)、雅格布•伯努利(Jacob Bernoulli)的遗著《猜度术》( J. Bernoulli’s Ars Conjectandi)，以及欧拉与拉格朗日的著作。这时，高斯也开始了他自己的研究。3年以后，高斯离开了学院，到Göttingen(哥廷根)大学就读。但当时高斯还尚未决定到底是专攻数学还是专攻语言学，直到他发现可以用圆规和直尺画出正十七边形(正多边形的欧几里德作图理论)的一刹那，才最终选择数学作为其职业生涯。

在当时，他进入了这样的一种状态，觉得有必要把他在此期间所产生的许多想法一一如实地记录下来。他的科学日记就是他自己研究成果的有力证明，并一直延续到1800年。这也是他一生中最多产的一个时期。在他已经完成的许多最重要的工作之中，几乎从来没有后人彻底地加以改进过，尤其是他对椭圆函数的考察。在此期间取得的成就，也包括他已经写成的《整数论研考》，该书在1801年出版。尽管当它出版的时候，能够看懂的人不多，但这并没有影响到人们一致公认为他是一位杰出的数学家。

1798年，高斯完成了他在哥廷根大学的学业，返回布伦瑞克。他仍然依靠所获得的那笔资助基金从事研究工作。1799年，他被赫尔姆施泰特(Helmstedt)大学授予博士学位的时候，本人并不在场。1801年，由于高斯的计算，使得失踪了的小行星谷神星(Ceres)再次得以发现，这件事使高斯名声大震。这是皮阿齐(G. Piazzi，意大利天文学家)发现并于1801年1月1日公布但随即消失了的一颗小行星。高斯要真正看到它是根本不可能的，他只是在此基础上，即凭借皮阿齐的有限的观察资料，进行理论和数据的考察与推断，从而成功地计算出它的运行轨道(注：1978年，当这颗小行星的反射光线再次出现时，Ceres专门撰写了有关的论文，由此而得以Ceres的名义命名)。此事的成功，使得高斯转向天文学方面的研究，从而使自己系统地深入到天文科学，并于1807年被任命为哥廷根天文台台长。这一职位一直被保留到1855年高斯逝世为止。这一职位使他能进行独立的大量的研究，而无需承担任何教学任务，但也必须做许多具体的行政工作。

正如我们所知道的，长期以来，数学与其背景密不可分。在德国北部地区的大面积测地工作消耗了高斯的许多时间，但人们可能不会看到高斯所卷入的这些实际问题却剌激了高斯在数学方面的某些研究。例如：在不同的几何方面，高斯把曲面上的问题映射到平面上，并在1816年左右就得到非欧几何的原理。他对测地线的观察剌激了许多数学技术的发展，也有助于高斯本人掌握巨大的实验资料。大地测量学是高斯在一生中通过一百多万次的计算而建立起来的。不过，如果高斯不做那些具体工作，而把他的全部精力都投身于数学的话，对数学的发展是否会更好一些。

我们已经看到，高斯的一生几乎没有发生过意外的重大变化。他一直在哥廷根度过了50年，并且在最后的几十年里实际上没有离开过这座城市。他的生活是清淡而朴素的，但是他也以此节俭的方式积累了一些财富，这也许是他在那种贫穷的环境中所养成的一种习惯吧！

尽管他的生活是普通的，但是他个人对他家庭的安排，以及他与另一些科学家之间的关系并不是和谐的。这里，我们主要对一封信感兴趣。该信是1838年11月高斯写给迪里赫列德的。我们已经指出，高斯不是很关注其他数学家的工作，这样说并非夸张。Jacobi抱怨高斯说，他没有引证过他和迪里赫列德的任何论文长达20年之久。他在阿贝尔(挪威，Abel)在世时没有给予任何关注，仅仅当阿贝尔英年早逝之后高斯请求他的挚友Olbers给他找一下，是否可以从哪里获得阿贝尔的肖像。对于法国数学家，或许由于政治上的原因，高斯至少是漠视他们的；而对于某些人，高斯甚至表现出莫大的厌恶。爱森斯坦是在公开场合受到高斯赞扬的少数人之一。然而他是不幸的，因为患病而意志消沉。在许多方面，爱森斯坦与高斯恰恰相反，因为他的著作与高斯“宁肯少些，但要好些”的格言格格不入。

这似乎很奇怪，高斯并没有公布他的许多重要的发现，尽管他在追求优先权方面要超过另一些数学家，且从未表现过厌倦。这会带来许多的麻烦，为此，他常常遭到非难。越到年老，高斯越是强烈地滋生那些似乎是不可能的与达不到的荣誉感。他的学生本来就少，但每当他可能与他们联系的时候他也总是回避不见。他对汉堡德•亚历山大表现出像冰川一样的冷漠。他不幸的家庭关系也许是造成他性格冷漠的因素之一。到目前为止，我们可以看到，高斯的青年时代和在哥廷根的前期已经从沉重的生活困境中解放出来，因而显得很幸福。在1805—1809年间，他与Johanna Osthoff的第一次婚姻期间，他们度过了一段彼此间感到美满而宁静的生活。高斯永远也不会忘记当他的第三个孩子刚刚诞生不久之后，他的第一个妻子就去世了(注：她生有二子一女)。不久，高斯再婚。然而，他与Minna Waldeck的第二次婚姻实际上是不幸福的。Minna长期生病，还时不时地会发作歇斯底里症。高斯与她所生育的孩子们的关系也很紧张，最终他们都离开高斯永久定居在美国。高斯写信给他在哥廷根求学时代就结下了友谊的好友Wolfgang Bolyai说：“我的一生，在这世界上的许多人，他们都妒忌我。这是真的！但我确信，这些痛苦的经历，已经相去甚远；只要在年轻时敢于与它们抗争，到老来所得到的，真正是价值无比。”

(2015年5月25日收稿)

参考文献

[1]SCHARLAU W, OPOLKA H. From Fermat to Minkowski [M]// Lectures on Theory of Numbers and Its Historical Development. New York: Springer-Verlag, 1985: 13-31.

[2]谢国芳. 高斯、爱森斯坦和二次互反律的“第三个”证明——一幕小戏剧[EB/OL]. (2012-08-15)[2015-05-25]. http://www.xieguofang. cn/Translations/Math/Gauss_Eisenstein_Ch.htm.

[3]KLINE M. Mathematical thought from ancient to modern times [M]. New York: Oxford University Press, 1990.

[4]华罗庚, 王元. 数论在近似分析中的应用[M]. 北京: 科学出版社, 1978: 128-129.

[5]潘承洞, 潘承彪. 初等代数数论[M]. 济南: 山东大学出版社, 1991: 112-117.

[6]唐志华, 徐沥泉, 徐利治. 欧拉应用分析于数论研究综述[J]. 南京师范大学学报: 自然科学版, 2007, 26(6): 43-48.

[7]徐沥泉, 林益, 吴仲和. 数论中三个著名级数定理的构造性证明及其推论[J].大学数学, 2010, 30(3): 123-128.

[8]MANIN Y I, PANCHISHKIN A A. Introduction to modern number theory [M]. 2nd ed. Berlin Heidelberg: Springer-Verlag, 2005: 115-189.

(编辑：沈美芳)

Gauss number theory studies and his life addendum

JIN Yanan①, XU Liquan②
①Wuxi Higher Vocational School of Tourism & Commerce, Wuxi 214045, Jiangsu Province, China; ②Wuxi Institute of Education Science, Wuxi 214001, Jiangsu Province, China

As we know, Carl Friedrich Gauss was a mathematician to make use of mathematical analysis to research the number theory after Euler and Lagrange. An introduction of his study is presented systematically here. There are many exciting formulas and theorems such as the constructability of the regular 17-gon, Gaussian sum and the law of quadratic reciprocity. His main numbertheoretical work, Disquisitions Arithmeticae, and several smaller number-theoretical papers contain so many deep and technical results that Fundamental Theorem of Algebra and the ring of Guassian integers and so on. These conceptions, theorems, and formulas were all fi rst discovered accurately by Gauss’ demonstrations. Gauss was extraordinary at converting a complex question into a simple problem. In fact, Gauss’ ideas have become more generalized. These facts are enough to prove that he had extensive and deep knowledge of his subject. A few instances represent his deep insight. Besides, we can appreciate the basic principle of methodology from Gauss’ inventions and discoveries. He never takes a process of discovery in a cover-up, and we know this from his diary which informs us about his most important discoveries.

Disquisitions Arithmeticae, the regular 17-gon, the law of quadratic reciprocity, Guassian sum, the ring of Guassian integers

10.3969/j.issn.0253-9608.2015.05.005

†通信作者，E-mail：liquanwx@163.com