能源电力衍生品的设计、定价及风险管理

□蔡 强 邓光军 邓世杰

[1.四川广播电视大学 成都 610073；2.电子科技大学 成都 610054；3.佐治亚理工大学 亚特兰大 美国]

引言

电力是现代社会发展不可或缺的基本能源，发电和电网等电力基础设施具有天然的垄断地位。为打破电力市场的自然垄断，提高资源利用效率，自上世纪八十年代，西方国家开始实施厂网分开、输配分离、竞价上网的电力工业市场化改革[1]。英国1989年颁布《电力法》要求建立竞争性电力市场和独立的管制制度。欧盟在“1996欧盟电力改革指令”中明确要求其所有成员国“建立一定的有效监管机制，保证透明度，以避免滥用某些垄断市场的行为，尤其是损害消费者、带有掠夺性的行为”。美国在1992、1996年先后公布和实施了《能源政策法案》、888号和889号法令（美国联邦能源管制委员会，Federal Energy Regulatory Commission，FERC）以建立竞争性的电力批发市场，并成立独立电力市场管理机构（Independent System Operator，ISO），负责调度①、电网运行、提供输电服务和阻塞管理、购买和提供辅助服务、通过市场平衡电网的实时供需关系，并进一步在1999年，FERC颁布法令建立区域输电组织（Regional Transmission Organization，RTO），经营与管理跨州电力调度。总之，电力工业包括发、输、配、售4个环节。各国电力市场基本上针对这4个环节进行不同方式和不同程度的改革[2]。

通常电力销售末端直接面对消费者，电力价格通常由政府采取管制措施。同时，消费者也倾向于签订长期合同以固定电力价格（例如，签订所谓的满载需求合同，Load-serving full-requirement contracts）。而在发电环节，常常采取竞价上网的交易机制。在电力输、配环节，由于供电与用电区域通常不在一个区域，经常存在供电和用电的不平衡并导致电力输送阻塞，进而导致不同区域间供电价格和用电价格存在差异。因此，在电力输、配环节也可采取市场竞争的方式确定价格。另外，在市场中参与电力交易通常为发电商、电力负荷服务商（包括电网送电和配电）和电力交易商，前两者具有实际的实物资产（如电力设备），在市场中充当对冲者（hedger），而后者纯粹是为了参与市场交易的资本雄厚的财团，在市场中扮演着投机者（speculator）的角色。

一、电力现货市场及其运作

在各国电力市场化和市场监管法案的推动下，西方国家先后成立了对应的电力现货批发和零售市场，如美国PJM电力市场、英国英格兰和威尔士（E&W）电力市场、北欧电力市场（Nord Pool）、澳大利亚国家电力市场、新西兰电力市场等。下面以美国PJM市场为例分析电力现货市场。

美国现有PJM电力市场、纽约州电力市场和新英格兰电力市场，它们彼此独立，市场模式大致相同[3]。3个市场中，美国的PJM市场最具有代表性。PJM电力市场指宾西法尼亚－新泽西－马里兰联合电力市场，是北美最大的电力联营体。PJM市场的参与者包括发电商、电力负荷服务商（包括电网送电和配电）和电力交易商，前两者提供发电和供电服务，后者只参与电力产品的买卖。发电商以市场价卖电，电力负荷服务商购买电力再卖给最终消费者，电力交易商多为实力雄厚的财团，也参与电力市场的买卖。

电力现货市场价格的形成有其自身特点[4]。在一个电力输送网络中，各个节点所对应的发电厂和用电消费区域存在着不平衡，所以各个节点的电力价格也不一样。每个节点可以看做一个小的完全竞争市场，通过市场作用形成的电力价格称为节点电价（locational marginal pricing，LMP）。在整个电力网络中，电力会从低价格节点向高价格节点流动，由于竞争和市场作用，在弥补了电网损耗和排除线路容量限制后，整个电力网络各个节点的电力价格应趋于“平衡”，即不存在套利的可能。

在各个节点通过电力现货市场交易形成节点价格。电力现货市场包括日前市场（day ahead，DA）和实时（real time，RT）市场，发电商、电力负荷服务商和电力交易商提前一日在日前市场上通过报价进行电力买卖，在当日的实时市场上根据实际情况再通过买卖对日前市场的交易做调整，最终形成节点电力价格。整个交易均由PJM的独立调度运营商（independent system operator，ISO）根据节点电价进行结算。由于实时市场滞后日前市场1天，因此，电力市场参与者赚取两个市场间的价格差，所得到的支付与期限为1日的期货收益相同。为了杜绝交易的信用风险，ISO通过严格的管理方式要求市场参与者对交易信用风险负责。ISO根据日前市场出清情况，并对次日的实际负荷做出评估和预测，在保证电力供应安全可靠的前提下，通知相关发电机组开停机。

电力市场参与者还可以针对电网不同节点间相互签订双边买卖合约以锁定价格，合约内容主要包括节点、电量、价格和交割时间，且交割时用现金交割。很显然，这种合约是非标准化合约而不具有流动性，难以实现价格发现功能。

除了基本的电力交易市场外，针对发电商，还存在容量信用市场(capacity credit market)，容量信用市场为供电企业履行可靠性协议规定的容量义务提供了买卖容量的机会。同时，还建立辅助服务市场，PJM目前建立了以市场报价为基础的调频服务交易市场。这两种市场都是为了市场电力运行平稳而设置的市场价格调解和调控发电的运行机制。

而针对电力负荷商，PJM开辟了输电权交易市场，输电权交易市场为输电网服务的用户提供了一个规避输电阻塞成本风险的机会。输电权是使用输电通道的权利，即拥有获得输电通道阻塞费的收入流的权利。PJM在日前市场及实时市场中对电能交易收取输电阻塞费用，并将这些阻塞费用分配给输电权拥有者。输电权交易市场中包括双边交易和输电权集中拍卖两种方式。

二、电力金融市场、期货和期权

根据前文电力生产、运输和配给特点可知，电力市场除了面临一般商品所面临的诸如市场需求波动性等特点之外，还包括电力自身特点所产生的风险。如由燃料市场波动造成的发电商发电成本风险、各电力运输节点电力价格差异造成的风险，电力需求具有高峰期、低峰期特征造成的需求波动风险等等。

为了规避电力市场风险，电力金融衍生产品应运而生。1995年，北欧电力交易所（Nordic Power Exchange）出现世界上第一份电力期货，1996年，纽约商品交易所（NYMEX）推出电力期权。当前几个交易电力衍生品的市场有：北欧电力市场（Nord Pool）、德国欧洲能源交易所（EEX）、法国电力交易所（Power Next）及加拿大天然气交易所（NGX）、纽约商品交易所、洲际交易所（intercontinental exchange,ICE）、澳大利亚股票交易所（ASE）、悉尼期货交易所（SFE）等为代表的电力衍生品交易市场。

由于电力网络及系统特有的复杂性，各个物理节点间供需不平衡导致整个网络中电力价格存在差异，难以形成统一的电力价格而不利于电力期货市场。为解决此问题，PJM把所管辖的电网建立了若干所谓的中心节点（实际是虚拟节点），该虚拟节点对应于相关多个实际物理节点。该虚拟节点的电价是这些物理节点LMP的加权平均，即中心节点的LMP是PJM电力市场的电价指数。基于中心节点的LMP可开发出各类电力金融衍生品。最常见的是电力期货和期权，这些电力金融衍生品都基于商品或金融期货和期权的概念发展而来。

首先是电力期货，电力期货包含以下几种：

1．根据到期日长短，分为日期货、周期货、月期货、季期货和年期货。

2．根据交割方式，分为物理交割和现金结算；由于电力不能存储，物理交割涉及到电力系统的调度，故多采用现金结算。

3．根据期货交割时段，又可分为峰荷（on-peak）期货和基荷（off-peak/base load）期货。所谓的峰荷期货，期货规定的交割时间为负荷较高时段的期货，而基荷期货是指交割时段为全天的期货。

电力期权分为看跌期权和看涨期权，或欧式期权和美式期权，但电力期权的标的物可以是电力现货和电力期货。由于电力无法存储的原因，又由于电力的实际消费量存在极其不确定性，因此，一方面需要通过市场价格机制对电网内部各节点间电力供给和需求进行调节以舒缓电网堵塞，另一方面通过ISO指令或根据电力交易商和发电商之间所签订的合约对发电设备进行开启和关停来适应电力需求的变化。为规避电力供给与需求间不平衡所造成的价格风险或电力生产成本的风险，针对网络堵塞，电力金融市场上开发出的金融产品有金融输电权（financial transmission rights,FTR）和关口权期权（flowgate rights，FGRs），对于发电商有点火期价差期权（spark spread option），电力交易商之间有摇摆期权（swing option）和电力租赁合约（tolling agreement）。下面，本文分别对它们做简要介绍。

点火期价差期权（spark spread option）是一个非标准化的电力期权，其标的资产价格是电力市场价格，其执行价格是燃料（天然气或石油）价格与热效率（heat rate）之积。点火价差期权到期时间T的支付为：

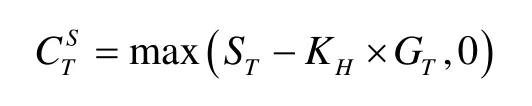
其中，ST是电力市场价格，KH是热效率，GT是燃料价格。发电商和电力交易商可以通过出售点火价差期权规避电力市场的价格风险。

发电商需要从燃料市场购买天然气或燃油产生电能，同时把生产出来的电能卖给电力负荷商，发电商的收益则取决于发电成本和电力市场价格，而发电成本和电力价格的波动来自于发电所需燃料价格和电力价格的不确定性。摇摆期权（swing option）为发电商规避两市场的价格风险提供了可行的手段。所谓的摇摆期权实际上类似于商品互换合约，该合约中规定了交易的起始和终止日期、交易的最大次数以及交易的总量和交割价格，但与互换合约不同的是摇摆期权具有更大的选择权（或灵活性）。即，在交易合约规定的起始和终止这段时间内，发电商（多头方）可以选择交易的时间、总的交割次数（但不能低于规定的最大交割次数）、每次交易的数量（必须在合约中规定的最小数量和最大数量范围内）。另外，发电商还可以把多购买电量再出售给卖方，同时，如果发电商交割数量低于或高于约定的数量范围则必须向卖方支付一定数量的罚金。

由于ISO要根据电力供需情况对电力系统的各个发电商发出关停或重启的指令，以确保电力供需平衡，这对发电商构成了运营风险。因此，结构化的双边交易是电力市场参与者分担和控制价格和数量风险的有力工具。其中最具创新的结构化交易合约是发电设备租赁合约（tolling agreement），其结构如下图所示：

图1 电力租赁合约

图1中，租赁合约期限长度为T。租赁合约赋予了合约持有者在合约期限内根据具体情况关闭或重启发电设备的权利，并且附加了诸多限制。首先，执行时点的限制。在租赁合约中规定了关停和重启的最大次数n，但每次执行的时机由合约持有者根据具体情况确定，最终选择执行的次数必须小于等于n。图中时间点t1、t2、…、tn表示选择合约执行的最佳时机。其次，由于每次物理关闭和重启发电设备不仅需要一定时间而且还必须支付一定的成本，还损耗发电设备的寿命，这些费用都必须由合约持有者承担。最后，发电过程中的发电成本需要合约持有者承担。这种结构化的租赁合约与摇摆期权一样，为合约的持有者提供了同时规避燃料市场和电力市场价格风险的作用。租赁合约的定价极具挑战性。由于可多次关停和启动发电设备，可以看做一系列的复合实物期权，其中的状态变量是燃料价格和电力价格。决策过程可采用动态规划方法进行优化，并采用仿真数值方法对合约进行定价。

点对点金融输电权（financial transmission rights,FTR）为输电商提供了风险规避工具[5～6]。在输电网络中各个节点间电力不平衡因而价格不一样，因而在特定的两个节点间由于网络阻塞会造成电力价格（LMP）差。在供需双方签订的双边协议中，发生阻塞时如果需求节点的LMP高于供给节点LMP高，则购电方将向供电方支付阻塞费用（两节点间的LMP之差与送电量之积）。这使得双边交易中购电方存在风险暴露。金融输电权可规避此类风险。如果购电方在签订双边交易合同并同时购买了金融输电权，那么当在双边实际交易中发生损失时可在金融输电权获得补偿。金融输电权到期时的支付正好是两个节点的电力价格差与输电权中约定的数量之积，期权合约中所规定交割节点与双边交易中的节点保持一致。只有当需求节点的LMP高于供电节点LMP时期权才会被执行并现金结算。

FTR建立在电网的两个节点上的输电权，而与电力实际输送所通过的具体节点和线路无关。为此，市场上又出现了把节点和电力输送线路结合在一起的关口期权（flowgate rights，FGRs）。由于到达目的节点所通过的中间节点的供给（或需求）以及线路的容量存在差异，必然会存在以各节点（包括起始节点和中间节点）LMP和线路容量所约束的路径和输电量优化等诸多问题，进而产生所谓的影子价格（即在有约束下最优化时的拉格朗日乘子）或机会成本。最终FGRs的价格即为影子价格。

FTR和FGRs两者从理论上都可以实现社会福利最大化，只是实现方法上存在差别，FTR操作相对简单容易，而FGRs存在优化过程而较为复杂。

三、电力价格运动模型

根据电力市场所面临的风险在国外电力市场已开发出比较成熟的风险管理工具（如前文所述），但这些诸如期货、新合约的交易需要进一步定价，而定价的基础必须对标的物（电力价格和其他因素）建立价格运动模型，本节将对电力价格进行论述。

用户对电力的需求会随着季节、天气、甚至节假日的变化而变化，既呈现出高度不可预测性，又呈现出周期性特征。这些特点造成了电力价格呈现出季节性、波动性、均值回复性及尖峰性等极其复杂的特征，对电力价格运动过程的描述及其衍生品价格的定价造成了巨大挑战。由于只有恰当地描述出电力价格才能对电力衍生品定价，因此如何从理论上描述电力价格的运动模式是一个关键性的基本问题。对于价格的波动性、均值回复性和跳跃性，在金融衍生品定价中，通常采用几何布朗运动、泊松过程和均值回复过程。现有的电力价格运动过程在这些基本模型的基础上，加入季节性和尖峰等特征。

为了描述季节性特征，Bhanot[7]采用工具变量（dummy variables）或线性分段常数函数（piece-wise constant function），Pilipovic[8]和Weron et al.[9]采用正弦函数（sinusoidal function），而Simonsen[10]和Weron et al.[11]利用小波分解（wavelet decomposition）刻画电力价格的阶段性结构（periodical structure）。

对于电力价格的尖峰特征，Clewlow & Strickland[12]，Johnson & Barz[13]、Eydeland & Geman[14]采用了跳跃过程来描述。Kholodnyi[15]利用非马尔科夫（non-Markovian）随机过程并考虑尖峰自回复性（self-reversing jumps）。Escribano[16]利用GARCH模型描述波动集群。最后，由Huisman & Mahieu[17]最早提出区域转换（regime switch）模型，随后被广泛地应用到电力价格模型（Huisman & De Jong[18]; Weron; Bierbrauer[19]; Haldrup & Nielsen[20]）。

下面，本节分别对Lucia & Schwartz[21]模型、Geman & Roncoronl[22]、Bierbrauer[23]等具有代表性的电力价格模型做评价和分析。

（一）Lucia & Schwartz（2002）模型

电力的需求变化又具有极强的波动性，波动性来源于季节性波动、气候变化、电网各节点供需不平衡造成的影响，这种波动性又具有周期性、重复性和短暂性特征。基于这些因素的考虑，Lucia & Schwartz分别建立了单因素模型、两因素模型，并对模型参数给出了估计方法。

Lucia & Schwartz首先利用均值回复过程建立了一个单因素模型，均值回复过程能够体现电力价格在经历波动偏离后回归到正常水平的趋势和特征。假设现货价格（spot price）为Pt，该价格包括两部分，确定部分f(t)和扩散随机部分Xt，即：

其中，κ＞0，X( 0)=x0，dz是标准Wiener过程增量。根据式（1）可得Xt=Pt-f（t），即：

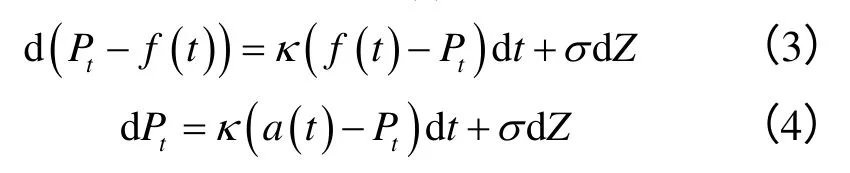
其中，a(t)是时间t的确定函数：

式（4）是一个典型的均值回复过程，其中，k表示现货价格Pt受到外界干扰后回归到固定均值a的速度。经过推导得到Pt的积分表达式并求得Pt的期望和方差：

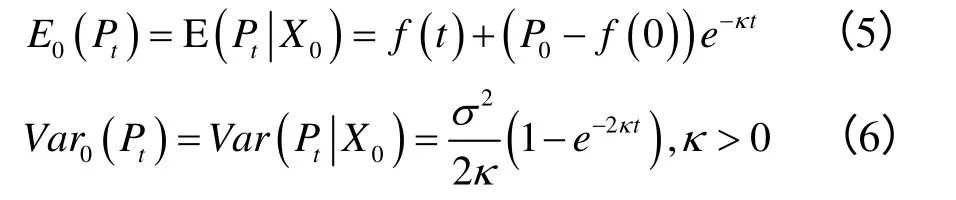
式（5）、（6）表明，随着时间t—＞∞，Pt回归于固定值f(t)，而Pt方差回归为σ2/2κ。

在以上模型的基础上，Lucia & Schwartz考虑了自然对数的单因素模型，即：

其中，f（t）同式（1），Xt服从式（2）定义的过程。可得：

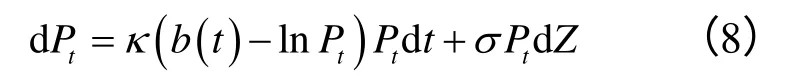
电力价格不仅存在长期回归，还存在短期回归现象，因此，Lucia & Schwartz进一步建立了现货价格的两因素模型。

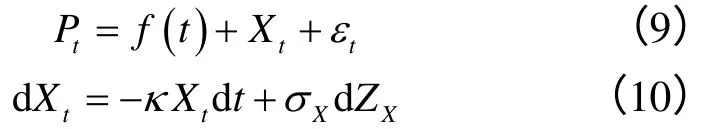
式（9）中的εt服从算术布朗运动：dεt=μtdt+σεdZε，dZXdZε=ρdt。对式（10）变形得：dXt=κ（α*-Xt）×其 中 ，λε分别表示与X和ε相联系的风险的市场价格。

（二）Geman & Roncoronl（2006）模型

Lucia & Schwartz利用他们的模型检验北欧电力市场价格时没有考虑价格的跳跃性。为此，Geman & Roncoronl对他们的模型进行了改进，他们的模型在考虑长期均值回复的基础上，不但考虑了尖峰上限及尖峰产生的长期频率和短期频率，还考虑了区域间的转换。Geman & Roncoronl用自然对数表示现货价格，并假设电力现货价格服从以下运动过程：

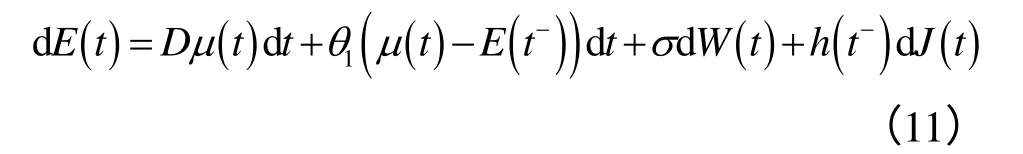
其中，D表示标准的一阶导数，f（t-）表示f在时间t的左极限。μ(t)表示可预测的现货价格的季节性变动趋势，式（11）第二项表示任何发生的波动都会回归到μ(t)，θ1> 0，度量回归的速度。σ是常数，dW是一个标准Wiener过程增量，表示不可预测的外部冲击。

除了式（15）所表示的回复过程外，式（11）中表示的运动过程的非连续部分也同样产生周期性尖峰效应。所谓的尖峰相对于一般的波动而言，价格首先是大幅度地向上冲击，然后再急速回归到正常水平。为表示该特有的过程可设立一个门槛值，如果价格低于这个门槛值，则价格处于正常波动区域且未来可能向上跳跃。但一旦价格突然发生向上的跳跃并超过该门槛值，那么可预见将来一定时间内必然会向下运动。这说明市场的供给和需求处于暂时非平衡状态而导致市场电力价格不正常。假设该门槛值为T(t)，定义符号函数h（E(t)） 表示跳跃方向：

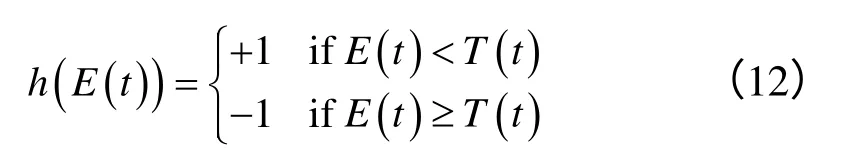
式（12）说明，根据现货价格E（t）是否大于或小于门槛值T（t），h（E（t））分别取+1或-1。

式（15）描述的跳跃过程除了方向外，还通常用发生时间、幅度等特征来刻画。为此，定义过程ι描述单位时间内发生跳跃平均次数，即：

其中，s(t)表示正常（和有周期可能）的跳跃强度形状（normalized jump intensity shape），θ2表示单位时间内最大的跳跃次数。跳跃的累计幅度用式（11）

中的dJ（t）复合泊松过程描述：Ji是一个独立同分布随机变量，它服从一般概率密度：

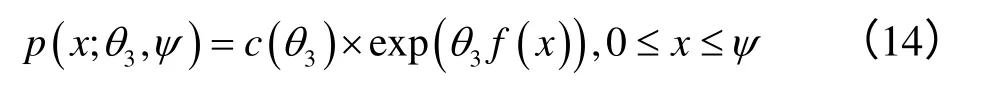
其中，c（θ3）是一个常数以确保p是一个概率分布密度，ψ是最大跳跃幅度。在指数密度函数家族选择截尾密度意味着可重复产生观察到的高阶动量（moments）现象。跳跃方向确定了关于电力价格水平跳跃幅度Ji的代数效应。

（三）Bierbrauer,Menn,Rachev（2007）

Bierbrauer,Menn,Rachev在分别讨论了均值回复过程和均值回复和跳跃混合过程的电力价格模型后，讨论了区域转换模型。在区域转换模型中，他们首先假设电力市场价格存在两种状态的情况，第一种状态是正常状态，第二种状态是外部冲击或跳跃造成的随机波动状态。状态之间的转换描述为马尔科夫链，其转换概率如下：

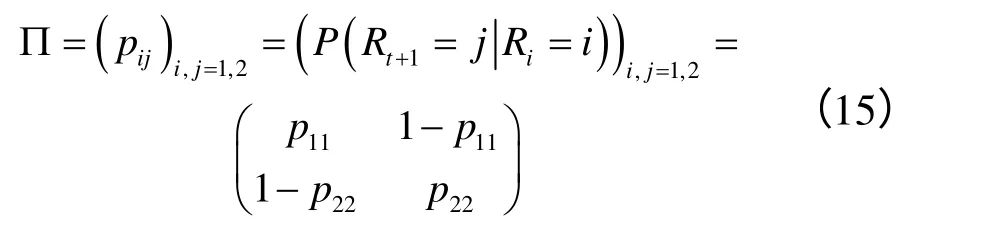
式（15）表示的是从时间t到t+ 1，从状态Rt=i转换到下一个状态Rt+1=j的条件概率。那么，从时间t到t+ 1，从状态Rt=i转换m个状态Rt+m=j的条件概率为：

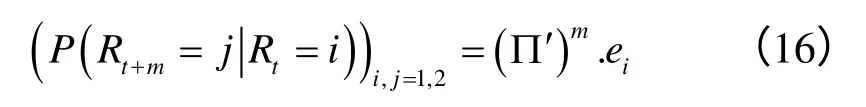
其中，∏′是∏的转置矩阵，ei是2×2单位矩阵（identity matrix）的第i列。在两种状态下存在两个不同的随机过程，Yt,1和Yt,2，分别由式（38）、（39）表示。

式（17）中，c、φ为常数，tε是标准正态分布（centered normal），F是尖峰（spike）的概率分布，可以选择正态分布或指数分布。注意，式（17）是标准Vasičk模型。那么，式（17）和式（18）间的转换概率为：

式（19）只表示从一种状态到另一种状态的单次转换概率。

还可以考虑3种区域：（1）基本区域（base regime），即Rt=1，描述电力正常动态变化；（2）初始跳跃（initial jump regime），即Rt=2，价格迅速上升或下跌区域；（3）回复跳跃区域（reversing jump regime），即Rt=3，价格在初始跳跃后回复到正常的基本区域。对于这三个区域，一旦价格发生跳跃，就会回复跳跃到正常过程，则其过程的转换概率依次为：P23=P31=1，P13=P21=0。三个区域的价格过程为：

其中，εt是均值为0、方差为σ2的独立同分布正态随机变量，ζt是均值为v、方差为τ2的独立同分布正态随机变量。

（四）评论

前面的三个代表模型基本刻画了电力价格的季节性、波动性、均值回复性及尖峰性等特征。不同的电力市场可能存在差异，这需要在对不同电力市场价格做出描述性统计的基础上正确选择模型形式，然后再根据实际电力市场价格数据对参数进行估计，进而获得合适的电力价格运动模型，最终为电力金融市场上衍生品定价提供基本支撑。

根据第一部分论述可知，电力相较于其他商品，有其自身特点：1.电力不能大规模存储，而由输电网络连接的供电和用电要求必须实时平衡；2.供电商、用电方位置的不均衡易导致电力供应不平衡；3.电力需求具有较低的价格弹性，消费者对电力需求受电价的影响小；4.电力价格归根结底由供需决定。供给方电力厂商的生产成本受到其他诸如煤炭、天然气和石油价格的影响，同时电力需求受到国家整体经济发展和人们生活水平提高的影响，这两者的影响构成电力价格可预测的长期运动趋势。

然而，现有的电力价格运动模型，对季节性、波动性、均值回复性及尖峰性等特征考虑较多，而对供需的交互以及电力运输和配给造成的价格变化特征考虑较少。这无疑是将来进一步研究的重点方向。

四、定价方法回顾和评论

在第三部分中已经看到，电力市场价格有其特殊而复杂的运动模式，采用一般商品或金融资产价格运动模式（如几何布朗运动、均值回复过程）对电力衍生品进行定价存在极大的偏差，而基于那些具体的运动模式对电力衍生品进行定价无疑具有极高挑战性。但尽管如此，依然有不断增长的文献对电力衍生品定价进行研究。归纳起来，这些研究的技术方法分为两类（Deng & Oren）[24]：（1）基本面方法（Fundamental approach），该方法依赖对市场和系统运行情况进行仿真以得到近乎真实的市场价格。（2）技术分析方法（Technical approach），正如前文所描述的那样，根据历史数据和统计分析来描述电力价格的随机过程。

基本面方法针对单一情况存在可行性，但如果可能的情况数量很大时，由于运算的复杂性将对仿真和计算造成极大负担。因此，在利用技术分析方法建立起电力价格运动模式的基础上，再结合其他诸如蒙特卡洛、格点（Lattice）方法对电力衍生品定价，则具有较强的可行性。

对于前文中的各种价格模型，最大似然估计方法能对那些离散模型的参数做出估计，但难以得到衍生品价格的解析表达式；而对于连续时间模型，模型参数需要基于动量（moment-based）方法估计，但没有最大似然估计方法有效。尽管如此，在各种扩散模型下，有许多定价方法依然被使用。

Deng[25]第一个利用仿射跳跃扩散（affine jump diffusion,AJD）在几种具体形式运动过程下（如区域转换、随机波动）建立了电力现货价格模型，并应用到了电力远期、买权/卖权和点火价差（spark spread）。Duffie et al.[26]把Deng的模型利用傅里叶转换做进一步扩展并得到了几种电力衍生品价格解析表达式。Kamat & Oren[27]得到了可赎回远期合约（callable forwards）的价格。

如果能获得大量的电力市场价格，对电力期权最适合的定价方法是推算出电力现货价格的风险中性分布，然后基于非套利原理获得电力衍生品价格。当无法得到市场未来价格信息则无法使用无套利方法，此时只能采用均衡定价方法（如Longstaff & Wang[28]、Lucia & Schwartz[29]、Bjork & Landen[30]、Bessembinder & Lemmon[31]、Kellerhals[32]）对远期价格和点火价差定价。在对具有复杂结构的电力期权（如摇摆期权（swing option）和租赁合约（tolling contract））的定价难以得到解析解的情况下，二项式/多维格点和蒙特卡洛仿真方法不失为可行的数值求解方法（Deng & Xia）[33]。

五、结束语

本文首先介绍国外电力现货市场现状，并讨论和分析电力衍生品市场所涉及到的包括期货、期权和结构化电力金融衍生品。然后，在仔细分析电力现货价格特征的基础上，对典型的电力现货价格模型进行了归纳和评论。最后对电力衍生品定价方法和技术做了讨论。

一方面，电力价格运动模型具有极强的复杂性，另一方面，电力衍生品具有多样性和复杂性特征，如结构化的电力衍生品。这两方面对电力衍生品的定价造成了极大的困难。在衍生品定价理论中，如何根据特定复杂的电力价格运动模型推算出电力现货价格的风险中性概率，如何构造无套利定价模型，如何采用均衡定价方法，这些问题都无疑是今后研究所面临的巨大挑战。

注释

①美国只有区域电力市场，尚未形成全国范围内的国家电力市场，但逐步扩大市场范围已成主要趋势。一方面，美国政府已经意识到区域市场间的协调在电网规划建设、区域市场运营等方面的重要作用，因而不断推动批发市场和RTO范围的扩大。另一方面，各区域电力市场之间也在逐渐加强协调与合作。

[1]马林峰.国外电力市场浅析[J].现代电力,2004,21(3):11-14

[2]马莉等.国外电力市场最新发展动向及其启示[J].电力系统自动化,2014,38(13):1-9.

[3]黄继明.美国PJM 电力市场探析[J].国际电力,2002,6(1):24-27.

[4]李道强,韩放.美国电力市场中的金融交易模式[J].电网技术,2008,32(10):16-20.

[5]方军等.输电阻塞管理的新方法述评(一):基于潮流的可交易输电权[J].电网技术,2001,25(7):4-8.

[6]张永平等.输电阻塞管理的新方法述评(二)：金融性输电权及与FGR 之比较[J].电网技术,2001,25(9):17-20.

[7]BHANOT K.Behavior of power prices:Implications for the valuation and hedging of financial contracts[J].Journal of Risk,2000(2):43-62.

[8]PILIPOVICH D.Energy risk:Valuing and managing energy derivatives[M].New York:McGraw-Hill,2007.

[9]WERON R.,BIERBRAUER M.,TRÜCK S.Modeling electricity prices:Jump diffusion and regime switching[J].Physica A,2004,336:39-48.

[10]SIMONSEN I.Measuring anti-correlations in the Nordic electricity spot market by wavelets[J].Physica A,2003,322:597-606.

[11]WERON R,SIMONSEN I,WILMAN P.Modeling highly volatile and seasonal markets:Evidence from the Nord Pool electricity market[C]//Takayasu H.(Ed.).The Application of Econophysics,Proceedings of the Second Nikkei Econophysics Symposium,Tokyo:2004:182-191.

[12]CLEWLOW L,STRICKLAND C.Energy derivatives:pricing and risk management[M].London:Lacima Publications,2000.

[13]JOHNSON B,BARZ G.Selecting Stochastic Processes for Modelling Electricity Prices[M].London:Risk Books,1999.

[14]EYDELAND A,GEMAN H.Fundamentals of Electricity Derivatives in Energy Modeling and the Management of Uncertainty[M].London:Risk Books,2000.

[15]KHOLODNYI V.Valuation and hedging of European contingent claims on power with spikes:A non-Markovian approach[J].Journal of Engineering Mathematics,2004,49:233-252.

[16]ESCRIBANO A,PENA J I,VILLAPLANA P.Modeling electricity prices:International evidence[EB/OL].[2015-01-30].http://www.researchgate.net/publication/4764394_Modeling_Electricity_Prices_International_Evidence?citationL ist=incoming.

[17]HUISMAN R,MAHIEU R.Regime jumps in electricity prices[J].Energy Economics,2003,25:425-434.

[18]HUISMAN R,DE J C.Option formulas for mean-reverting power prices with spikes[J].Energy Power Risk Management,2003(7):12-16.

[19]BIERBRAUER M,TRÜCK S,WERON R.Modeling electricity prices with regime switching models[J].Lecture Notes on Computer Science,2004,39:859-867.

[20]HALDRUP N,NIELSEN M.A regime switching long memory model for electricity prices[J].Journal of Econometrics,2006,135:349-376.

[21]LUCIA J J,EDUARDO S.Schwartz.Electricity prices and power derivatives:Evidence from the Nordic Power Exchange[J].Review of Derivatives Research,2002,5(1):5-50.

[22]GEMAN H,RONCORONI A.Understanding of the fine structure of electricity prices[J].Journal of Business,2006,79(3):1225-1261.

[23]BIERBRAUER M,MENN C,RACHEV S T,Truck S.Spot and derivative pricing in the EEX power market[J].Journal of banking & finance,2007,31:3462-3485.

[24]DENG S J,OREN S S.Electricity derivatives and risk management [J].Energy,2006(31) 940-953.

[25]DENG S J.Stochastic models of energy commodity prices and their applications:mean-reversion with jumps and spikes[EB/OL].[2015-01-30].http://citeseerx.ist.psu.edu/viewdo ewdoc/download?doi=10.1.1.16.1116&rep=rep1&type=pdf.

[26]DUFFIE D,PAN J,SINGLETON K.Transform analysis and asset pricing for affine jump-diffusion[J].Econometrica,2000,68:1343-1376.

[27]KAMAT R,OREN S S.Exotic options for interruptible electricity supply contracts[J].Operation Research,2002,50(5):835-850.

[28]LONGSTAFF F A,Wang A W.Electricity forward prices:a high-frequency empirical analysis[J].Journal of Finance,2004,59(4):1877-1900.

[29]LUCIA J J,SCHWARTZ E S.Electricity prices and power derivatives:evidence from the Nordic power exchange[J].Review of Derivatives Research,2002,5(1):5-50.

[30]BJRK T,LANDÉN C.On the term structure of futures and forward prices[C].//GEMAN H,MADAN D,PLISKA S,VORST T,eds.Mathematical Finance—Bachelier Congress.Berlin:Springer Verlag,2000:111-150.

[31]BESSEMBINDER H,LEMMON M L.Equilibrium pricing and optimal hedging in electricity forward markets[J].Journal of Finance,2002,57:1347-82.

[32]KELLERHALS B P.Pricing electricity forwards under stochastic volatility[EB/OL].[2015-01-30].http://papers.s srn.com/sol3/papers.cfm?abstract_id=274788.

[33]DENG S J,XIA Z D.A real options approach for pricing electricity tolling-agreements[J].International Journal of Technology & Decision Making,2006,5(3):421-436.