环境污染群体性事件的信息传播Kermack-Mckendrick模型

□刘金全 魏玉嫔

[吉林大学 长春 130012]

引言

随着经济的加速发展，改革开放的不断深入，我国既进入了发展黄金期，又进入了矛盾的凸现期，即德国社会学家乌尔里希·贝克提出的“风险社会”[1]。大量社会经济矛盾交织在一起，各类环境污染群体性事件发生概率呈上升趋势，严重影响到我国社会稳定和向现代化的平稳过渡[2]。这种风险的直接表现就是近年来全国各地环境污染群体性事件的频繁发生。实践表明，突发事件中政府的公信力和信息传播是突发事件应急处置的关键。针对环境污染群体性事件的危机管理是对政府部门处理复杂问题能力的现实考验，直接考验着政府部门在公共危机状态下能否用最短的时间控制局面，化险为夷，赢得转机[3]。正如英国危机管理专家里杰斯特指出，“只有进行有效的传播管理，才能进行有效的危机管理[4]。”

突发事件应急管理是近年来管理领域出现的新兴学科。在对突发性群体事件的研究中，大量文献运用动态演化系统和社会仿真分析方法研究了社会公共危机事件的信息传播特点和规律等[5～6]，运用博弈论和仿真分析方法分析了环境污染事件的协同演化机理和处置措施分析[7～8]。环境污染群体性事件具有高度突发性、信息匮乏或过剩、信息传播具有特定阈值等特征，现有文献针对环境污染群体性事件具有的信息传播特征进行理论研究取得成果尚不多见。近年来，国内外一些学者运用传染病传播模型，在复杂网络上研究有关社会谣言的传播问题[9～11]，将谣言传播问题纳入到管理科学领域的分析视野。本文根据环境污染群体性事件具有阈值性、谣言与真实信息相互作用等信息传播特征，在Kermack- Mckendrick传染病传播模型[12]的基础上，构建了政府施加控制之前和政府施加控制的信息传播模型，研究了环境污染群体性事件信息传播机制。最后，结合2009年河南省“杞人忧钴”事件作为算例，对环境污染群体性事件的谣言传播模型进行检验。

一、环境污染群体性事件信息传播模型

（一）基本假设

设总体群众人数为N，当有谣言传播事件发生后，在时刻t事件相关人群分成三类：

第一类：部分相关人群获悉该信息，同时该人群正在将此谣言告知他人。该类知情者是谣言传播者，其在人群所占比例记为I(t)；

第二类：已知该谣言但并不将该谣言传播给他人者。该部分不相信谣言的人群称为谣言中止者，所占比例记为R(t)；

第三类：不知道该谣言的人群所占比例记为S(t)。

假设A1：总体群众的人数为N，变量I(t),R(t),S(t)为连续可微变量。

假设A2：每一个谣言传播者可能会将此谣言传播给他想告诉的人。假设谣言传播者平均传播率为常数β，未知情者所占人数的比例是S(t)，故谣言传播者在单位时间内传播谣言的有效率为βS(t)。将谣言传播者将信息传播给I,R两类人时（该两类人均已知此信息）为无效传播。因此，单位时间内I类人群传播谣言给S类人群的总人数是βNS(t)I(t)，即单位时间内I类人群增加的数量。

假设A3：谣言传播者转换为谣言终止者R类的转换率正比于谣言传播者数量NI(t)，比例系数γ。

由此，可得环境污染群体性事件信息传播模型：

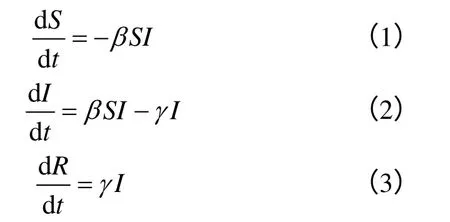
其中，S(t)+I(t)+R(t)=1，初值NS(0)=S0＞0,NI(0)=I0＞0,NR(0)≥0。参数β＞0称为传播率，γ＞0称为移除率，称为相对移除率。

方程（1）表示环境污染群体性事件中未知情者比例减少的速率；方程（2）表示谣言传播者比例的变化率；方程（3）表示谣言终止者比例增加的速率。

（二）环境污染群体性事件信息传播方程解的讨论

根据已有研究表明[13]，如果初始状态下未知情者所占人数比例小于相对移除率，S0＜ρ，则当t增加而趋于无穷时，谣言传播者的数量I(t)单调下降趋于零。

如果初始状态下未知情者所占人数比例大于相对移除率，S0＞ρ，则当t增加时，谣言传播者的数量I(t)增加到一定数量Imax后就单调减少趋于零，并且存在，它是下超越方程的唯一正根：

目前，公司生产的大口径离心球墨铸管、真空消失模管件、离心钢管和双金属复合管、钢塑复合管、覆膜管等产品填补了多项国际技术和产品空白，并开发出了国际第三代供水管道产品。公司还获得“第八届中国专利金奖”、国家科技进步二等奖、省长特别奖等30多项省部级以上奖励。持续不断创新，使企业的技术和产品始终引领行业发展。

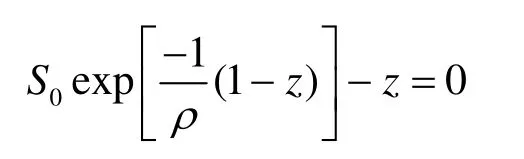
从图1中看出，如果初值（S0,I0）落在直线S=ρ的左边，随t增加I(t)单调下降趋于零，也即谣言的传播逐渐减少最终消失；如果S0＞ρ则相信谣言的人数I(t)先是逐渐增加，直到S通过ρ谣言传播者类的人数达到最大值后才开始下降，而后逐渐趋于零。

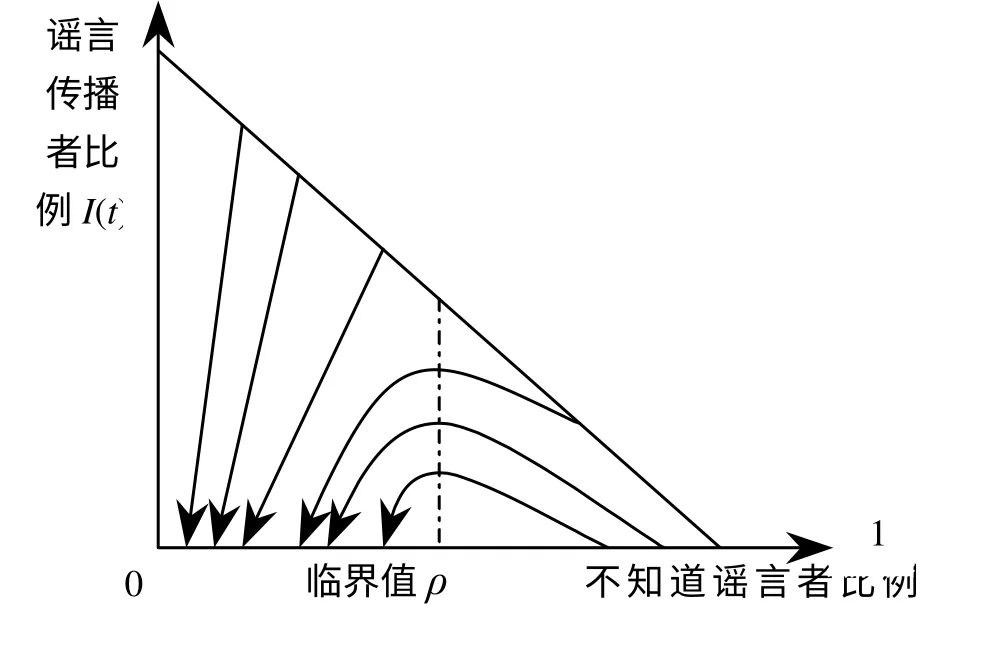
图1 环境污染群体性事件信息传播模型的解线族

定理1：在环境污染群体性事件信息传播模型中，当S0,I0为定值，ρ＜S0时，谣言传播者的数量I(t)所达到的最大值Imax为ρ的减函数。

证明：由（1），（2）消去dt，可得：

当S=S0,I=I0时（4）的解为：

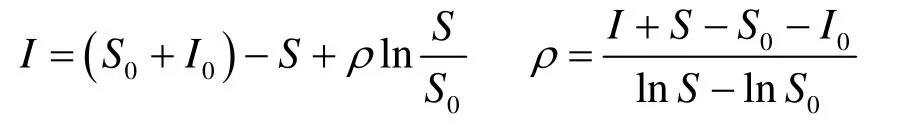
因为，当S=S时，I(t)为最大，此时：

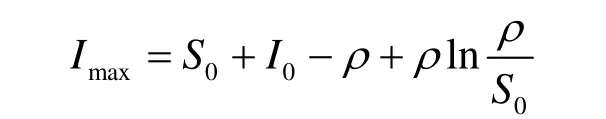
当ρ＜S0时，进行谣言传播的人数I(t)有一个高峰值。如果对谣言不施加控制，这就意味着相信谣言的人数的增加，从而引发大规模的社会恐慌，影响和威胁本地区甚至全国经济社会稳定和政治安定局面，有重大的社会影响。那么如何对此谣言进行控制，使得对任意初值（S0,I0）随t增加,I(t)单调下降趋于零，并且Imax=I0，或者使Imax控制在理想数值范围之内是十分重要的。地方政府进行信息传播过程控制的目的，就是要提高不信谣言者的人群数量阈值ρ，降低进行谣言传播人群的峰值Imax。

（三）政府部门辟谣措施后信息传播阀值分析

在环境污染群体性事件演化过程中，各类信息来源和传播渠道相互影响，当事者出于恐慌、愤怒、激动等非理性情绪和心理作用下，很容易造成各类小道消息或谣言的迅速传播。当有谣言传播事件发生后，地方政府或者权威机构需要及时发布官方权威信息进行辟谣，此时有一部分谣言传播者不再相信谣言，从而变成谣言中止者。

假设谣言传播者变成谣言中止者的概率为P，则地方政府控制措施后环境污染群体性事件的信息传播模型（2）（3）变为：

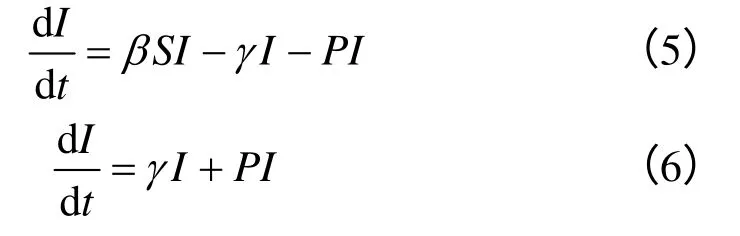
定理2：地方政府控制措施后的信息传播模型（5）和（6）中，当P=β(S0-ρ)时，Imax=I0,谣言传播者人数随着时间t增加而减少，当t趋于无穷时，谣言最终消失。当P＜β(S0-ρ)时，I(t)人数仍有一个高峰值。

因此，对谣言传播模型施加控制时，必须满足一定条件，才能有效地控制Imax，防止此谣言蔓延，最终达到消除此谣言的目的。

二、以河南省“杞人忧钴”事件为例

（一）事件回顾及传播数值假设

2009年6月7日2时，开封市杞县利民辐照厂发生卡源故障。2009年7月10日开始，一则题为《开封杞县钴60泄漏》的帖子在各大网络论坛流传。2009年7月12日，开封市政府就杞县利民辐照厂卡源故障举行首场新闻发布会，表示卡源情况不属于辐射事故。2009年7月16日，国家环保部派专家及机器人赶赴杞县利民辐照厂。2009年7月17日上午，“杞县发生核泄漏”、“杞县核泄漏造成多人死亡”等谣言，开始通过互联网和手机短信流传。2009年7月17日，由于担心和恐慌“核泄漏”，成千上万名杞县的群众冒着40多摄氏度的高温逃离家乡，外出避难，杞县县城一度空城，上演了一幕现代版的“杞人忧天”，又被称为“杞人忧钴”事件[14]。

（二）谣言传播过程的数值分析

梳理整个“杞人忧钴”事件，谣言是引发大规模社会恐慌的主要诱因。此次危机事件的发展分为以下三个阶段。

第一阶段，环境污染群体事件爆发期（6月7日-7月12日）：由于人们不明真相，奔走相告，此时虚假信息的传播非常快，传播率要远远大于0(β>>>0).由于政府此前没有对事故处理情况的信息做及时有效的发布，那么信息的移除率为0（γ=0）。此时方程（2）谣言传播者的增加率按照β的概率直线上升，而根据方程（3）谣言终结者比例增加的速率为0，即没有谣言终结者。在此发展阶段，“钴6O泄漏直接辐射”、“杞县核泄漏”、“核爆炸”等虚假信息通过网络、手机短信等多种渠道迅速传播，加剧了此次放射源被卡事件发展的不确定性和风险，使得事态逐渐滑向失去监督和控制的边缘。最终酿成了一起重大的环境污染突发性恐慌事件。

第二阶段，环境污染群体事件扩散期（7月12日-7月17日）：此阶段地方政府信息控制措施无效。7月12日，由于当地政府部门举办了一场信息简单和传播渠道单一的新闻发布会，再无其他举措。此时，谣言移除率γ＞0，但是由于不能满足当地群众对于相关信息的急切而强烈的需求，反而客观上佐证了杞县确实发生了发射源被卡事故，导致传播率远远大于移除率，即此时，相对移除率远远小于信息开始时的传播量，即ρ＜S0。根据定理3，随着时间的推移，ρ会逐渐增大，随着ρ的增大，谣言者的传播数量I（t）人数会达到一个高峰值Imax，进而导致流言的扩散和恐慌的增加，政府和传统媒体公信力下降，危机进一步加剧，相关处理应对工作也将变得更加复杂和棘手。

第三阶段，环境污染群体事件恢复期（7月17日-7月18日）：此阶段地方政府采取了有效的信息控制和引导措施。事态恶化后，当地政府迅速采取各种措施进行辟谣，开始通过电台，电视、网络、手机、宣传车等多种渠道公开信息、澄清真相。7月18日，开封警方宣布“抓获杞县钴60事件5名造谣者”，其中一名曾经传播虚假消息的网友被拘留。截至18日凌晨3时，杞县外出的绝大部分群众已经返回家中，杞县社会秩序稳定。由于政府有效控制，β在逐渐减小，γ，ρ在逐渐增大。当谣言传播者变成谣言中止者概率P达到P=β(S0-ρ)这个阀值的时候，谣言传播者人数随着时间t增加而减少，当时间足够长时，谣言最终消失。

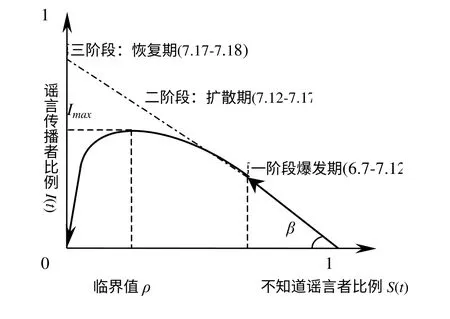
图2 “杞人忧钴”事件谣言传播的演化相图

地方政府作为环境污染群体性事件的管理者，在整个突发事件应对过程中发挥着至关重要的角色。对“杞人忧钴”事件的算例分析，验证了信息传播模型的基本结论：（1）如果地方政府在处理环境污染群体性事件时，第一时间没有采取有效的控制和引导措施，那么谣言“绑架”公众的强烈破坏作用很快就显现出来，导致环境污染群体性事件的爆发。（2）地方政府采取的控制措施是否有效，主要取决于地方政府的公信力、信息透明度和是否多渠道发布信息和应急能力等因素。

三、结论

本文研究表明，地方政府采取权威信息发布渠道等辟谣措施后，增大了谣言传播者变成谣言中止者的概率，从而降低了谣言传播比例的峰值和阈值，有利于事态的恢复和平息。但是，本文尚未考虑复杂的人际关系网络（即环境污染事件在复杂网络上信息传播规律）、谣言的反复性和不同类型、信息传播与政府应对措施的协同性等问题，这些将在未来深入研究。

在互联网时代，各种新的信息媒介和信息来源空前广泛，因此，在处理环境污染事件以及与人民群众密切相关的其他重大消息的问题上，政府不能再因循守旧、墨守成规。在网络信息时代，各级政府应努力提高对谣言突发事件处置能力，包括建立新闻宣传绿色通道，发现倾向性苗头迅速采取措施，及时通过媒体平息谣传；组织相关人员收集并分析研判网上舆情，做好正面宣传工作；做好信息监测、分析、会商和信息报送等，从而努力在事态的萌芽期加以有效处置和控制。

[1]乌尔里希·贝克.自由与资本主义[M].杭州:浙江人民出版社，2001.

[2]刘德海.群体性突发事件中政府机会主义行为的演化博弈分析[J].中国管理科学,2010,18(1):175-183.

[3]SCANLAN L H.Public relations in crisis and disaster[J].Public Relations Review,1999,25(2):251-252.

[4]迈克尔·里杰斯特.危机公关[M].上海:复旦大学出版社,1995.

[5]李志宏,王海燕,白雪.基于网络媒介的突发性公共危机信息传播仿真和管理对策研究[J].公共管理学报,2010,7(1):85-93.

[6]钟琪,戚巍,张乐.Lotka-Volterra 系统下的社会型危机信息扩散模型[J].系统工程理论与实践,2012,32(1):104-110.

[7]刘德海.环境污染群体性突发事件的协同演化机制[J].公共管理学报,2013,10(4):102-113.

[8]刘德海,陈静锋.环境群体性事件“信息-权利”协同演化的仿真分析[J].系统工程理论与实践,2014,34(12):3157-3166.

[9]BARTHELEMY M,BARRAT A,PASTOR- SATORRAS R,VESPIGNANI A.Velocity and hierarchical spread of epidemic outbreaks in scale-free networks[J].Phys.Rev.Lett,2004,92:178701.

[10]YAN Gang,ZHOU Tao,WANG Jie,et al.Epidemic spread in weighted scale-free networks[J].Chinese Phys.Lett,2005,22:510-513.

[11]WU F,HUBERMAN B A,et al.,Information flow in social groups[J].Physica A,2004,337:327–335.

[12]杨光,张庆灵.对传染病数学模型（Kermack_ Mckendrick 模型）施加控制的阈值分析[J].生物数学学报,2004,19(2):180-184.

[13]陈兰荪,陈键.非线性生物动力系统[M].北京:科学出版社,1993:111-124.

[14]孙丽娟.突发事件中政府不能失语：以“杞人忧钴”事件为例的个案分析[J].新闻爱好者,2010(1):73.