一种基于空域滤波的米波雷达测高新方法

吴剑旗，杨雪亚

(华东电子工程研究所 合肥 230088)

0 引言

由于米波雷达的波长较长，具有良好的反隐身和对抗反辐射导弹的能力[1]，近年来受到了广泛的关注和应用。现代米波三坐标雷达的一个关键问题是低仰角测高。但是受阵列孔径和机动架设的限制，米波雷达波束宽，角分辨率低。此外，米波雷达受地面反射多径的影响较大，中低空探测时波束打地，强相关的直达波和地面反射波同时进入接收波束主瓣，导致波瓣分裂[2]。因此，米波雷达测高的难点是在低角度分辨率、低仰角及不同粗糙程度的反射面条件下完成对目标高度的高精度测量。

由于回波中所携带的关于目标仰角的相位信息被多径回波所破坏，单脉冲测角技术[3-4]会带来很大的测高误差。直达波和多径反射波的波程差通常小于一个距离分辨单元，无法利用时延估计方法[5]从到达时间上进行分辨。阵列超分辨技术已应用于多径信号的波达方向估计问题中，代表性的算法有线性预测算法[6]，空间平滑多重信号分类[7-8](MUSIC)算法，以及最大似然[9-10]类参数估计方法等。但是这类算法通常需要特征值分解和多维空间谱搜索，不利于工程实现，且受反射多径影响较大，在低仰角、复杂阵地环境下测高性能严重恶化。波瓣分裂法[11]利用直达波和反射波产生的分裂波瓣，通过简单的相位比较和查表处理估计目标高度，然而，该方法对反射阵地的平坦度及雷达架设高度要求苛刻。文献[12]给出了一种高确定性的回波信号模型及其似然函数求解方法，可以利用阵地的起伏程度和反射系数等信息改善最大似然算法的测高精度，不过在实际工作中很难获得阵地环境的先验信息。

空域滤波技术[13-14]可有效地抑制空间干扰和噪声，增强有用信号。本文将空域滤波引入到米波雷达测高中，由于测高过程在脉冲压缩和时域滤波之后进行，目标回波信噪比通常较高。将目标直达回波和反射多径回波看作两个未知方向的旁瓣干扰，在仰角搜索过程中形成零陷分别对应于当前搜索仰角及其多径反射角的空域滤波器，并对阵列数据进行空域滤波。当波束零陷刚好将回波信号对消掉时，滤波后能量最小，正角度零陷对应的仰角即为目标仰角。相比较传统的米波雷达测高算法，本文提出的方法具有阵地适应性强、测量精度高及运算复杂度低等优点。

1 信号模型

垂直放置的均匀线阵(ULA)由N个间距为d的阵元组成，阵列参考点高度为ha。假设阵地反射面为平坦反射面，远场窄带的目标回波信号分别经直达路径Rd和地面反射路径Rs入射到阵列，目标高度为ht，对应的入射俯仰角为Ψ=[φd，φs]，其中φd和φs分别为目标的直达波和地面反射波的俯仰角，如图1所示。

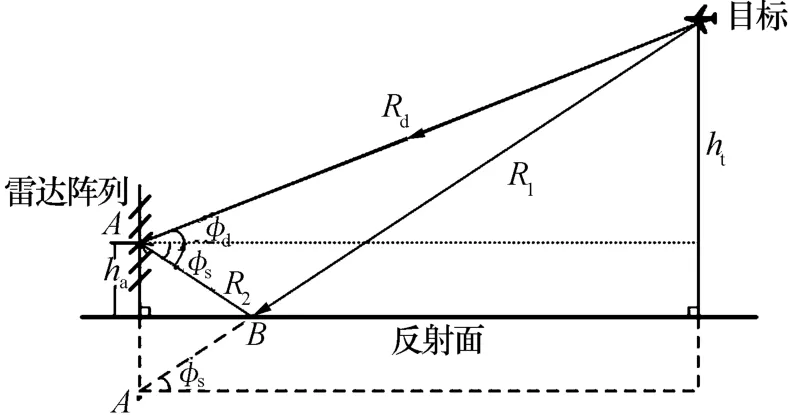
图1 阵列天线接收信号电波传播示意图

阵列接收的回波矢量为

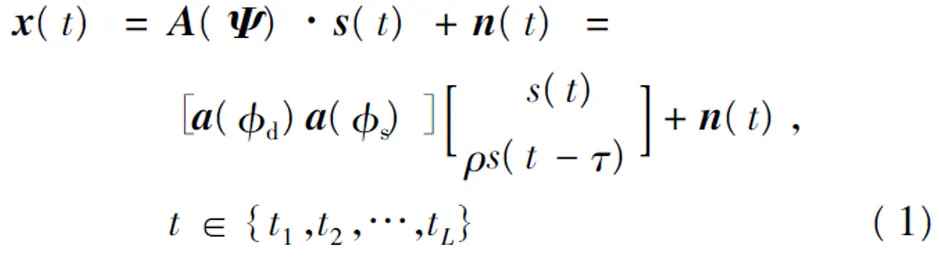
其中

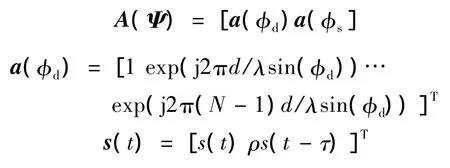
式中:A(Ψ)为阵列流型矩阵;a(φd)为阵列对目标直达波的导向矢量;(·)T表示转置;a(φs)为对应反射波的导向矢量;s(t)为目标回波复包络向量;ρ为反射区的反射系数;τ=ΔR/c，为波程差引起的时延，其中ΔR=Rs-Rd=R1+R2-Rd;n(t)是与信号不相关的复高斯白噪声向量。N×L的数据矩阵X=[x(t1)，x(t2)，…，x(tL)]表示L快拍的阵列数据。

当地面粗糙度增加到不再满足瑞利准则时，来自于目标到达粗糙面上的信号不是完全的镜面反射，同时在其他入射角上被散射，此时雷达天线接收的信号应该是镜面反射分量与漫反射分量之和。将式(1)信号模型写成矢量形式

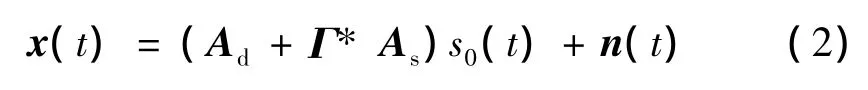
式中:Ad=a(φd);Γ为反射系数向量;*表示Hadamard积，为多径反射向量之和，其中a(β)=[1，ej2πdsinβ/λ，…，ej2πd(N-1)sinβ/λ]T，g(β-φs)为多径反射角分布函数。显然，当反射面完全平坦时As=a(φs)。

阵列协方差矩阵由式(3)进行估计

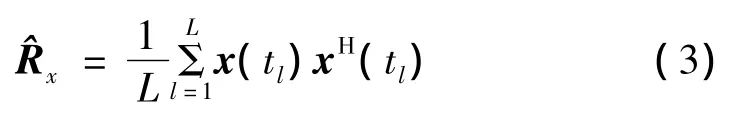
式中:(·)H表示共轭转置。

2 空域滤波测高方法

目标直达回波和多径回波可视为从不同仰角进入的干扰，可使用空域滤波方法进行对消处理。目标在测高过程中，需要进行角度搜索，设搜索仰角为φi，根据图1所示的几何关系，镜像反射角度φj为

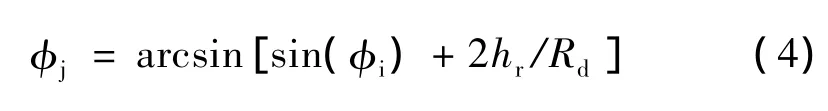
通过式(4)将φi和φj二维角度搜索转化为一维搜索，有效降低了运算量。

仰角搜索范围内的任意角度φi∈Φd，Φd为直达波的角度搜索范围。构造“干扰”的协方差矩阵如下

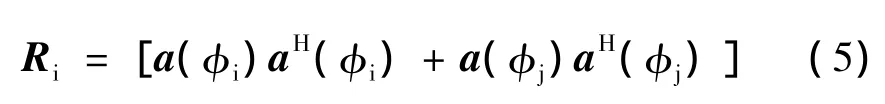
算法的目标是求空域滤波器系数向量Wi，使指向为φb的滤波器对消掉仰角φi和φj处的干扰，即求解如下基于最小噪声方差的准则的解

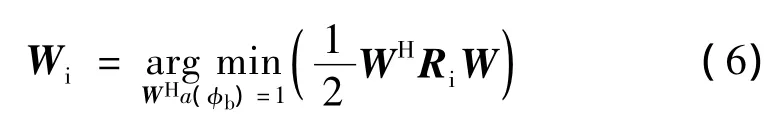
式中:W为空域滤波器系数向量的搜索范围。

其中

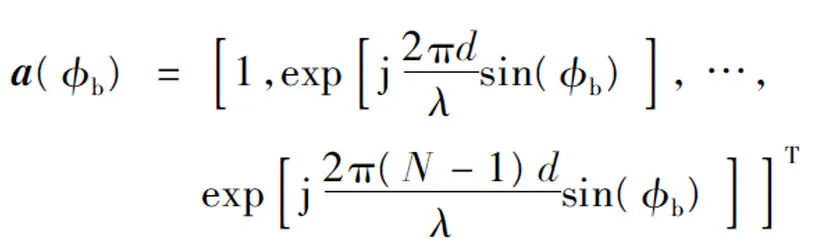
应用拉格朗日乘子法，代价函数表示为

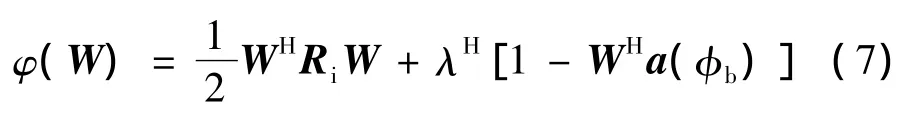
对φ(W)的W求导，并令其为0，则有

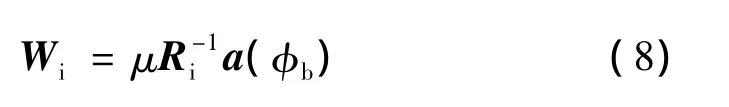
其中

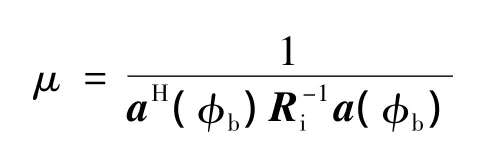
通常使用对角加载技术[15]提高滤波器的稳定性、降低副瓣电平，式(5)修正为

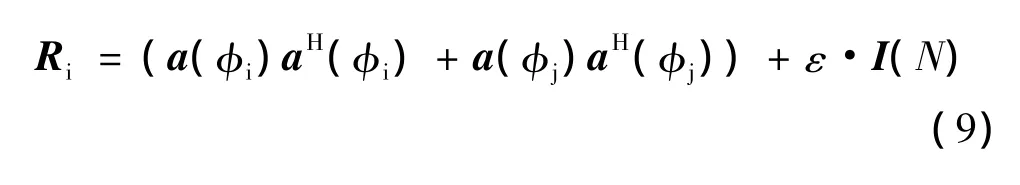
式中:I(N)为N×N的单位矩阵;ε为很小的正常数。

使用Wi对阵列接收回波数据进行滤波处理，滤波后的能量为

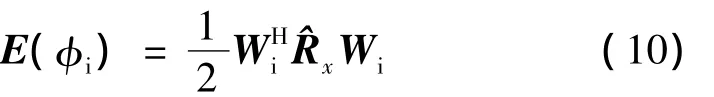
当φi=φd、φj=φs时，空域滤波器的两个零陷刚好将直达回波和多径回波对消掉，剩下的只是噪声，此时滤波后的能量最小。因此，向量E的最小值对应的正零陷角度即为直达波入射角的估计值d。然后，可计算球面模型下目标的高度

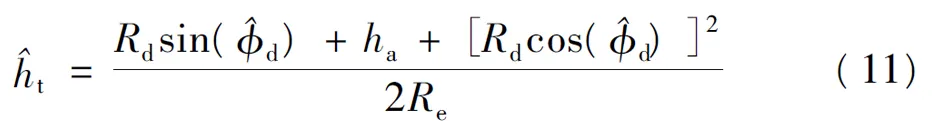
式中:Rd为脉冲压缩处理得到的目标距离;Re为地球等效半径，Re=4/3×6371km。

关于滤波器指向的选取，主要考虑以下两个方面:

(1)每个搜索仰角对应的滤波器指向φb要远离零陷φi，以免产生波束指向偏移和波束响应畸变;

(2)尽量靠近“干扰”角度φi，以保证较大的干噪比和良好的对消效果。

结合理论分析和实测数据处理结果，选取φb∈(φi+φ3dB/2，φi+φ3dB)是较为合理的，其中φ3dB是波束宽度为3 dB的指向角。

3 实验结果分析

下面通过仿真和实测处理结果验证本文方法的有效性，分别在平坦反射面和粗糙反射面时将本文方法和传统的超分辨算法进行性能比较。

仿真实验中所采用的阵列是垂直放置的均匀线阵，阵元数为30，阵元间距半波长。设目标距离280 km、高度10 000 m、仰角φd=1.10 °、多径入射角φs=-1.12°、地面反射系数ρ=-0.9。单元天线的直达波信噪比为5 dB，10个采样快拍。图2a)给出了搜索仰角φi=1.0°时空域滤波器的响应曲线，在角度φi=1.0°及其对应的反射角φj=-1.01°处分别形成零陷。图2b)是空间平滑 MUSIC算法(SS-MUSIC)、最大似然算法(ML)及本文的空域滤波方法的空间谱对比，每种算法的极值点用圆圈标示，虚直线是目标真实仰角位置。从图2b)可以看出，和SS-MUSIC及ML算法相比，空域滤波算法的测角结果更接近于真实值。

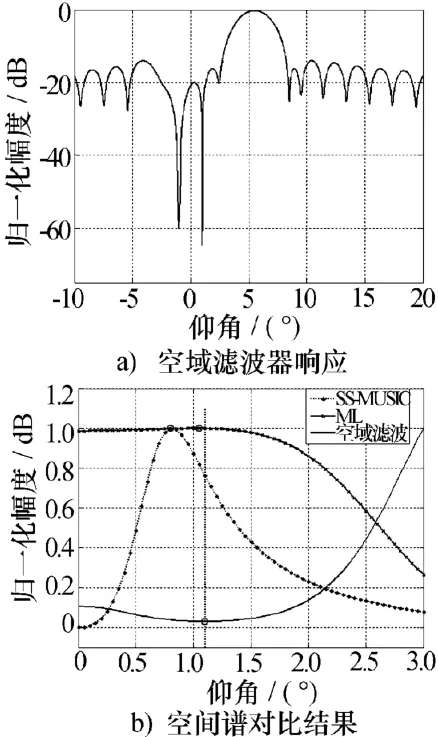
图2 平坦反射面时角度测角结果

利用米波雷达采集的实测数据验证本文方法的有效性。图3是雷达架设在开阔平坦阵地时对某批民航飞机的观测结果，其中图3a)为目标角度估计值随目标距离的变化，图3b)为测高结果随目标距离的变化，其中基于应答信号的二次雷达曲线是目标仰角和高度的真实值。从图3可见，在平坦反射面条件下最大似然和空域滤波方法的测高性能接近，而SS-MUSIC算法的测高误差随着目标仰角的减小迅速增大。图4给出了雷达架设在粗糙反射阵地时的处理结果，阵地周围分布建筑物和植被，容易引起散射和漫反射现象。由于在复杂阵地环境下回波模型严重失配，SS-MUSIC和ML算法已经无法分辨直达波和多径反射波，导致测角和测高误差非常大。与之形成鲜明对比的是，本文的空域滤波测高方法测量的高度和目标真实高度吻合较好，在1.0°以下的超低仰角区，测高均方根误差在600 m以内，显著改善了角度分辨率和测高精度。从以上实测数据处理结果可见，传统的超分辨算法对反射面起伏敏感，而空域滤波测高方法在平坦阵地及粗糙阵地均能得到良好的测高效果，显示了其对阵地反射面较强的适应性。

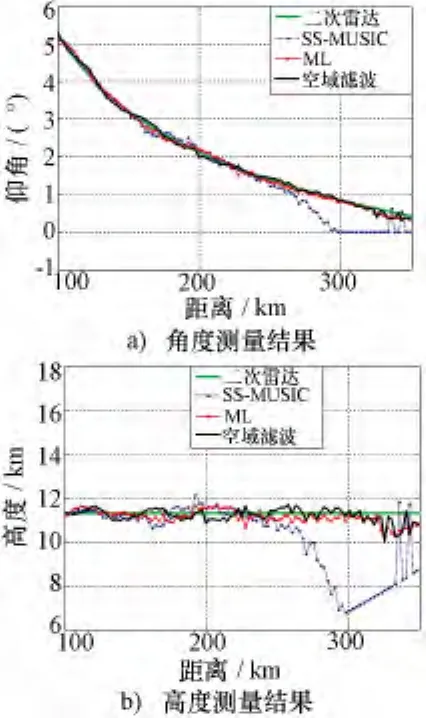
图3 平坦地面的测高结果

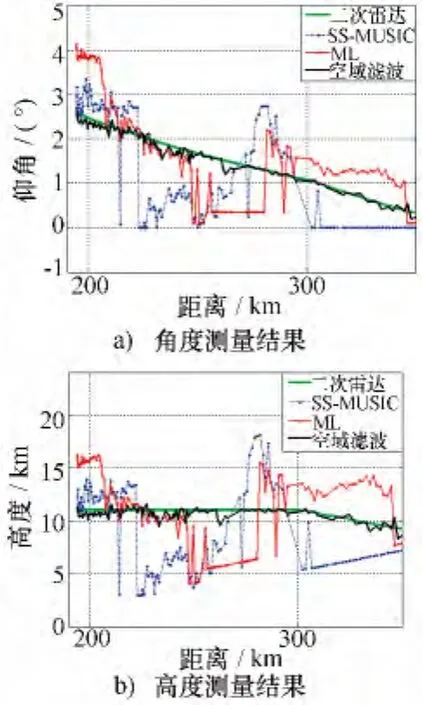
图4 粗糙地面的测高结果

4 结束语

地面反射尤其是粗糙反射面引起的多径信号是米波雷达测高中最主要的问题，因此本文提出了一种基于空域滤波处理的测高算法。该算法将目标回波作为干扰处理，在仰角搜索过程中形成在直达角及其反射角处具有两个零陷的空域滤波器，并对阵列接收信号进行滤波处理，通过搜索滤波输出最小值的位置估计目标仰角和高度。与其他的超分辨测高算法相比，本文提出的方法运算复杂度低，并且具有较高的角度分辨率和测高精度，并通过仿真及米波雷达实测数据分析结果得到了验证。

[1]Kuschel H.VHF/UHF radar part 2:operational aspects and applications[J].Electronics and Communication Engineering Journal，2002，14(3):101-111.

[2]陈伯孝，胡铁军，郑自良，等.基于波瓣分裂的米波雷达低仰角测高方法及其应用[J].电子学报，2007，35(6):1021-1025.Chen Baixiao，Hu Tiejun，Zheng Ziliang，et al.Method of altitude measurement based on beam split in VHF radar and its application[J].Acta Electronica Sinica，2007，35(6):1021-1025.

[3]Zheng Y B，Tseng S M，Yu K B.Closed-form four-channel monopulse two-target resolution[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39(3):1083-1089.

[4]Rocca P，Manica L，Martini A，et al.Design of compromise sum-difference patterns through the iterative contiguous partition method[J].IET Microwaves，Antennas and Propagation，2009，3(2):348-361.

[5]Ge F X，Shen D X，Peng Y N，et al.Super-resolution time delay estimation in multipath environments[J].IEEE Transactions on Circuits and Systems，2007，54(9):1977-1986.

[6]Xin J M，Sano A.MSE-based regularization approach to direction estimation of coherent narrowband signals using linear prediction[J].IEEE Transactions on Signal Processing，2001，49(11):2481-2497.

[7]Thakre A，Haardt M，Giridhar K.Single snapshot spatial smoothing with improved effective array aperture[J].IEEE Signal Processing Letters，2009，16(6):505-508.

[8]Dai J，Ye Z.Spatial smoothing for direction of arrival estimation of coherent signals in the presence of unknown mutual coupling[J].IET Signal Processing，2011，5(4):418-425.

[9]Stoica P，Sharman K C.Maximum likelihood methods for direction-of-arrival estimation[J].IEEE Transactions on A-coustics，Speech and Signal Processing，1990，38(7):1132-1143.

[10]Forster P，Larzabal P，Boyer E.Threshold performance analysis of maximum likelihood DOA estimation[J].IEEE Transactions on Signal Processing，2004，52(11):3183-3191.

[11]Chen B X，Zhao G H，Zhang S H.Altitude measurement based on beam split and frequency diversity in VHF radar[J].IEEE Transactions on Aerospace and Electronic Systems，2010，46(1):3-13.

[12]Lo T，Litva J.Use of a highly deterministic multipath signal model in low-angle tracking[J].Radar and Signal Processing，IEE Proceedings F，1991，138(2):163-171.

[13]Nai S E，Ser W，Yu Z L，et al.Iterative robust minimum variance beamforming[J].IEEE Transactions on Signal Processing，2011，59(4):1601-1611.

[14]Tao J W.Performance analysis for interference and noise canceller based on hypercomplex and spatio-temporal-polarisation processes[J].IET Radar，Sonar and Navigation，2013，7(3):277-286.

[15]Elnashar A，Elnoubi S M，El-Mikati H A.Further study on robust adaptive beamforming with optimum diagonal loading[J].IEEE Transactions on Antennas and Propagation，2006，54(34):3647-3658.