海上风机结构工作模态识别的组合降噪方法
2015-05-16董霄峰练继建王海军
董霄峰,练继建,杨 敏,王海军
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
海上风机结构工作模态识别的组合降噪方法
董霄峰,练继建,杨 敏,王海军
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
海上风机结构现场原型观测所获取的振动加速度信号中,往往混有大量的电磁工频、机组转频及环境噪声等成分,这些干扰信号处理不当易导致模态识别失真与产生虚假模态等问题.针对这一问题提出了基于自适应滤波与集成经验模态分解(EEMD)法的组合降噪方法.通过对测试信号采取滤波、分解、降噪及重组等过程可以更有效地降低各种噪声干扰,以完整地保留结构自身的振动信息;再利用随机减量法(RDT)和特征系统实现法(ERA)完成模态信息的初步识别,并结合振型分析等手段剔除虚假模态,实现准确提取海上风机结构工作模态参数的目的.该方法相比传统的降噪方法在噪声统计特征不足情况下具有更好的降噪精度和降噪效率,对基于实测信号获取风机结构工作模态信息有很好的工程应用价值.
海上风电;模态识别;自适应滤波;集成经验模态分解;振型分析
结构工作模态参数既是体现结构运行状态下振动动力特性的重要指标,也是对结构运行安全性检测和评估的必要前提.近年来通过现场试验采集环境荷载激励下的结构响应来识别结构工作模态成为学者们研究的重点.文献[1-5]中就分别对海洋平台、泄流状态下的高拱坝、桥梁以及陆上风机等结构的模态参数进行了识别,均取得了显著成果.
海上风机结构由于同时受到风、浪、流甚至更复杂环境激励的联合作用,其在运行过程中可能产生不健康甚至危害风机正常工作的振动,因此在运行阶段对风机结构进行实时的安全监测与状态评估具有重要意义.由于发电机组与支撑结构紧密相连,因此在运行状态下海上风机结构的响应具有其独特的特点,一方面外部环境激励下结构会产生振动,另一方面还受到机组运行荷载与电磁荷载的影响,同时信号中还掺杂环境噪声的干扰.本文对江苏启东海域已建某海上风电试验样机进行现场原型观测试验,获得了结构在不同运行工况条件下的动力响应信号,针对加速度信号中电磁工频、机组转频与环境噪声等成分联合干扰易导致模态识别失真与产生虚假模态等问题,提出基于自适应滤波与集成经验模态分解(ensemble empirical mode decomposition,EEMD)法的组合滤波降噪思路.该方法可以更加有效地降低各种噪声的干扰以完整保留响应信号中体现结构自身振动的信息,再结合随机减量法(random decrement technique,RDT)和特征系统实现法(eigensystem realization algorithm,ERA)对重构信号进行模态识别,最后利用振型分析等方法剔除机组转频等干扰引起的虚假模态,实现准确提取结构模态参数的目的.本降噪方法相比传统方法在噪声统计特征不足情况下有更好的降噪精度和降噪效率,对基于实测信号获取风机结构工作模态信息也具有良好的工程应用价值.
1 工程概况
所测试的海上风电试验样机位于江苏启东海域,基础采用天津大学自主研发的复合式筒型基础形式[6-7],机组为永磁直驱型风力发电机组,额定功率2.5,MW,额定转速 18,r/min.测试风机叶轮直径93.4,m,轮毂高度 80,m,塔筒分 3段安装,每一段塔筒的下部均设有工作平台.
根据实际测试环境,本次测试沿塔筒方向布置测点,测点数量 5个,具体布置见图 1.传感器选择LC0,461型低频压电式加速度传感器,频响范围可以达到 0.1~1,000,Hz,均为 3向测振(x、z向为水平方向,y向为竖直方向),满足采集结构低频多向振动信号的试验目的.本次测试获取的信号为风机运行状态下受外界环境荷载激励产生的振动响应,为避免风机较高转速工况下强谐波激励影响造成的模态识别失真,本文仅选取若干低转速工况下结构x向振动响应作为研究对象,该运行状态下风机结构振动具有明显的低频特性.测试采样频率为200,Hz,每组工况稳定测试时长60,s,现场测试典型工况参数及响应主频率见表1.

图1 现场测点布置Fig.1 Layout of field testing

表1 现场测试典型工况信息Tab.1 Information of typical conditions in field testing
2 降噪理论与应用实例
2.1 降噪理论
假定一条由不同频率成分组成的染噪信号 ()xt,各频分对应信号均为零均值平稳过程,其表达式可以写为各单一频率信号与噪声的累加之和,即

式中:n为信号中所有频率的个数;if为各单一频分信号对应的频率;iφ为每个频分对应的相位角;为各频分信号中含有的噪声信号.
EEMD方法具有较好的抵抗信号分解时各阶信号分量中产生的模态混叠现象[8],因此可利用 EEMD法对原始信号 ()xt进行分解.当信号中添加的白噪声尺度合理(通常加入噪声标准差为原始信号标准差的0.2倍[9]),且经过足够多次的集成平均后,理论上可以获得m(m ≤ n)个单一周期或频分清晰的染噪信号 xi(t),每个 xi(t)即为原始信号的一阶分解分量

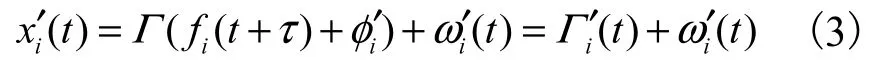

均方误差输出的均方值为
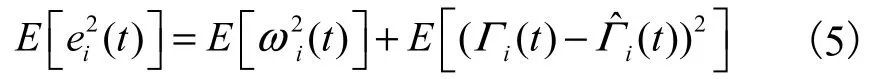

按照以上降噪思路处理,可以得到m个滤波降噪后不同频分特征的信号分量,将各阶分量重构后即可以得到最终的滤波降噪信号

2.2 应用实例
为了验证本文组合降噪方法的适用性和优越性,本节分别对一条由多频分组成的染噪信号与一条实测信号进行降噪处理.构造染噪信号频率成分包括0.5、1.5、2.5、10.0和45.0,Hz,信噪比设为10.0,信号采样频率 100,Hz,采样时间 5,s.实测信号选择典型工况1中 1#测点x向振动信号为研究对象,分别采用“EMD+小波”方法[12]、小波阈值方法和本文方法对上述两种信号进行降噪处理,得出降噪后信号的信噪比与降噪前后信号间的互相关系数,见表2.

表2 各方法降噪后的信噪比与互相关系数Tab.2 Signal-noise ratio and cross correlation function of the de-noising signals by various methods
由表2可以看出,经过本文方法处理后获得的信号信噪比与互相关系数结果更优,说明本文提出的降噪方法相比于其他方法能够在保证信号最大程度完整性的前提下,达到最佳降噪效果.其主要原因是经EEMD分解后的信号分量极大地改善了经验模态分解中的模态混叠现象,使得分解的低频分量主要为单一周期性的窄带信号,再对信号降噪时能更加有效地发挥自适应噪声抵消器的作用.该方法不仅避免了小波降噪时阈值选取不当造成有用信号损失及经验模态分解降噪方法的盲目性,而且提高了噪声统计特征不足情况下信号的降噪效率,同时以原始信号作为降噪参考使得信号降噪的精度和准确性得以保证.
3 海上风机结构工作模态识别流程
在进行模态识别之前,需假定风机叶轮转频及其倍频谐波频率在识别过程中引起的虚假模态为谐波模态,在模态识别过程中与结构真实模态能够同时提取[13].根据实测海上风机结构振动加速度响应的特点,依据自适应滤波、EEMD、模态参数识别等理论,本文确定实测信号组合滤波降噪及结构工作模态参数识别方法的流程如下.
(1) 对于实测的加速度动力响应信号,先通过自适应滤波中的陷波器理论去除 50,Hz电磁工频及其100,Hz倍频干扰信号.
(2) 对过滤信号进行 EEMD分解,由于其具有较好的抵抗临近频域内模态混叠的能力,使得每个低频分量都是仅包含单一频分或频分清晰的染噪信号.
(3) 依据自适应噪声抵消器理论,对信号每阶分量延迟并进行降噪处理,同时去除原始响应信号在分解时产生的明显高频噪声分量和残量,将降噪后的各分量重组为新的信号.
(4) 选取适宜长度的信号时程,利用 RDT法可获得滤波降噪后响应的衰减信号,通过奇异熵增量对系统阶次定阶,构造相应 Hankel矩阵再结合抗噪能力较强的ERA方法实现结构模态参数的初步识别.
(5) 将 5个测点同方向信号识别得到的振型系数组成结构各阶模态振型,通过判断分析结构各阶识别振型并结合数值模拟结果与 MAC准则来剔除机组转频和残余噪声引起的虚假模态,精确获取海上风机结构运行状态下的模态参数.
本文信号滤波降噪与风机结构工作模态参数识别流程如图2所示.

图2 海上风机结构工作模态参数识别流程Fig.2 Procedure on the operational modal identification of the offshore wind turbine structure
4 海上风机结构模态参数识别
以表 1中的典型工况1为例,图 3为该工况下4#测点x向滤波信号经EEMD分解后的各阶低频信号分量的功率谱密度,可以看出信号分解后低频分量基本为单一频分的信号,这些频分中既包括结构真实模态频率,也可能含有外界干扰引起的虚假模态信息. 提取各测点 x向滤波降噪后的信号,根据 RDT法取信号前 10,s作为输入数据的时间长度,计算出各测点对应的自由衰减信号,即为结构各阶模态分量响应的自由衰减信号之和,可作为结构工作模态参数识别的基础,其中 1#测点 x向滤波降噪后局部信号的自由衰减信号时程如图4所示.
根据文献[3]中提出的奇异熵增量理论,依据各测点对系统进行定阶,如图 5所示,可以看出当系统阶次为12阶时,奇异熵增量均小于0.05并开始降低到渐近值,此时信号的有效特征信息量已经趋于饱和,特征信息基本完整,去除非模态项和共轭项后,实际得到该结构振动系统的阶次为 6阶.考虑到结构系统定阶后仍有可能包含噪声模态,因此还需要利用文献[14]中提出的模态置信因子MAC准则对识别的模态参数进行判别,剔除噪声引起的虚假模态,最终可得到结构前4阶模态振型.

图3 各阶低频分量功率谱密度Fig.3 PSD of low frequency components

图4 自由衰减信号时程Fig.4 Time history of free decay signal
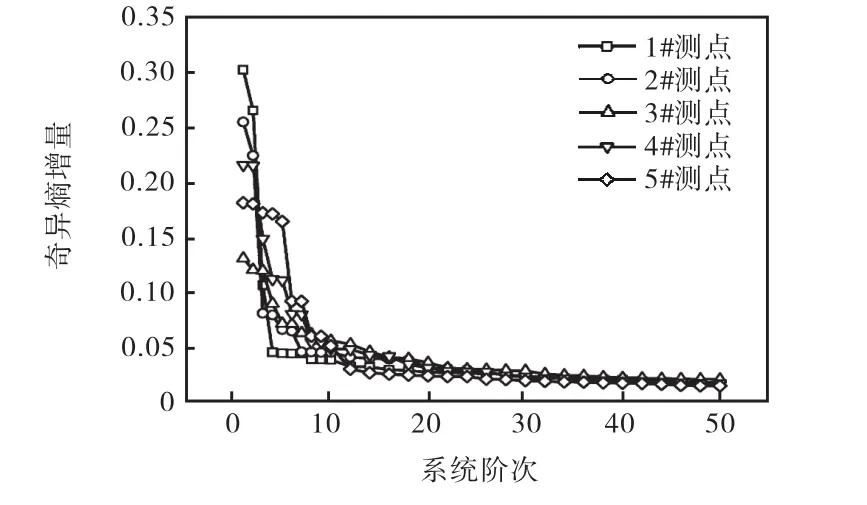
图5 信号奇异熵增量Fig.5 Increment of singular entropy
图6给出了识别的前4阶模态振型与风机结构数值模拟得到的各阶模态振型结果,可以看出通过实测数据识别得到的结构第 1、4阶主振型分别为塔筒结构正向的第 1、2阶弯曲振型,其对应的识别模态频率范围分别为0.33~0.35,Hz和2.52~2.59,Hz,与数值模拟振动形式基本相同,为结构真实模态.第 2阶主振型为侧向的2阶弯曲振型,对应的识别频率范围为1.39~1.45,Hz,与数值模拟结果一致.第3阶主振型为结构的1阶弯曲振型,对应的识别模态频率范围为 1.88~2.06,Hz,该振型处于第 2、4阶模态的 2阶弯曲振型之间,考虑风机结构可近似成以基础为固定约束的简单低频柔性悬臂梁结构,因此该阶主振型可以判断为不合理的虚假模态振型,其产生原因应该是由机组转频的倍频谐波成分所引起.表 3为在典型工况1下基于不同测点x向的振动响应,识别获得海上风机结构前 3阶工作模态频率和阻尼比信息.根据以上方法与思路,工况2~工况4下1#测点x向信号所识别的模态结果参见表 4.可以看出测试风机结构前 3阶频率范围分别为 0.33~0.35,Hz、1.41~1.43,Hz及2.52~2.53,Hz,与工况1识别结果范围较为相近,并且与表1中风机结构振动的主要频率特性保持一致.同时,识别的各阶模态阻尼比基本均在合理范围之内,说明本文的工作模态识别结果真实可靠.
图7为针对现场测试各典型工况下1#测点的实测数据,分别采用第2.2节中3种不同的降噪方法对信号处理后,再采用第3节中的方法进行风机结构工作模态识别所获得的各阶模态频率比对.从图中可以看出,采用小波阈值方法和“EMD+小波”方法对原始实测信号进行降噪处理后,前3阶模态识别频率变化较不稳定,特别是第 2、3阶模态出现了明显的大幅度的模态频率识别波动.而通过本文降噪方法对实测信号处理后的识别频率随外部环境条件的波动较小,说明该降噪方法对海上风机结构工作模态的稳定识别具有更好的工程适用性.

图6 结构前4阶振型Fig.6 The 1st four mode shapes of structure

表3 工况1下信号模态参数Tab.3 Structural modal parameters under condition 1

表4 工况2~工况4下1#测点x向信号模态参数Tab.4 Structural modal parameters of measuring point 1 in x direction under conditions 2—4
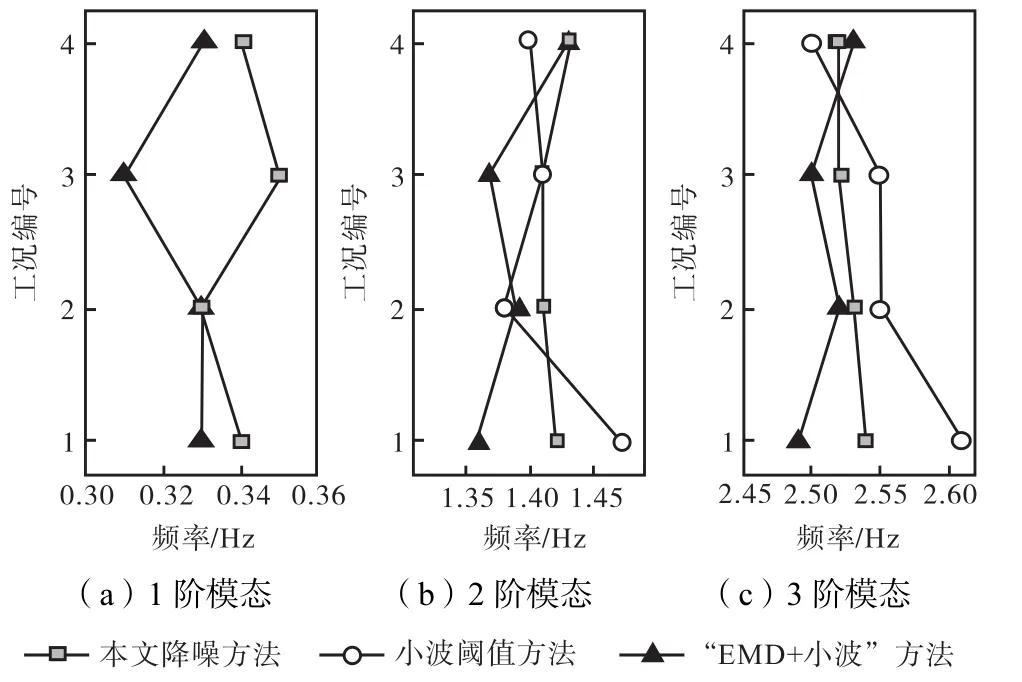
图7 不同方法降噪后各工况前3阶模态识别结果Fig.7 Results of 1st three identified modes of each condition using differ-ent de-noising methods
5 结 论
本文以某海上风力发电试验样机原型观测振动数据为研究对象,引入自适应滤波与 EEMD联合方法对实测信号进行滤波降噪处理,并针对结构工作状态下的模态参数进行识别研究,从而得到以下主要结论.
(1)自适应滤波与 EEMD方法联合的实测信号滤波降噪方法在滤波方面针对性更强,最大程度地保留了信号的完整性.在降噪方面提高了噪声先验知识不足情况下信号的降噪效率,同时又以原始信号作为降噪参考使得信号降噪的精度和准确性得以保证.
(2)针对机组转频及其倍频等干扰可能引起的虚假识别模态,利用振型分析来实现真假模态的判断,通过实际工程验证了本方法的可行性.
(3)经由本文组合降噪方法处理后,识别出不同工况下海上风机结构真实的前 3阶工作模态频率范围为0.33~0.35,Hz、1.39~1.45,Hz及2.52~2.59,Hz,结构阻尼比均在合理范围,说明该方法对于海上风机结构工作模态信息特征的精确和稳定识别具有很好的优越性和工程应用价值.
[1] Yang J N,Lei Ying,Pan S W,et al. System identification of linear structures based on Hilbert-Huang spectral analysis,Part 1:Normal modes[J]. Earthquake Engineering and Structural Dynamics,2003,32(9):1443-1467.
[2] 杨和振,李华军,黄维平,等. 海洋平台结构环境激励的试验模态分析[J]. 振动与冲击,2005,24(2):129-132.
Yang Hezhen,Li Huajun,Huang Weiping,et al. Experimental modal analysis of offshore platform under operational conditions[J]. Journal of Vibration and Shock,2005,24(2):129-132(in Chinese).
[3] Lian Jijian,Li Huokun,Zhang Jianwei. ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy[J]. Science in China Series E:Technological Sciences,2009,52(2):400-412.
[4] Li Hui,Li Shunlong,Ou Jinping,et al. Modal identification of bridges under varying environmental conditions:Temperature and wind effects[J]. Structural Control and Health Monitoring,2010,17(5):495-512.
[5] Adams D,White J,Rumsey M,et al. Structural health monitoring of wind turbines:Method and application to a HAWT [J]. Wind Energy,2011,14(4):603-623.
[6] Lian Jijian,Sun Liqiang,Zhang Jinfeng,et al. Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines[J]. Transactions of Tianjin University,2011,17(2):132-137.
[7] Lian Jijian,Ding Hongyan,Zhang Puyang,et al. Design of large-scale prestressing bucket foundation for offshore wind turbines [J]. Transactions of Tianjin University,2012,18(2):79-84.
[8] Yeh Jia-Rong,Shieh Jiann-Shing. Complementary ensemble empirical mode decomposition:A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis,2010,2(2):135-156.
[9] Wu Zhaohua,Huang N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis,2009,1(1):1-41.
[10] 陈向坚,高希复,刘长义. 自适应噪声抵消器在内燃机故障诊断中的应用[J]. 海军工程学院学报,1989(2):10-16.
Chen Xiangjian,Gao Xifu,Liu Changyi. Application on the fault diagnosis of internal combustion engine based on adaptive noise canceller[J]. Journal of Marine Engineering Institute,1989(2):10-16(in Chinese).
[11] 林家瑞,朱帆三,陈瑞红,等. 强背景噪声下微弱生理电信号的检测与处理[J]. 华中理工大学学报,1994,22(9):119-123.
Lin Jiarui,Zhu Fansan,Chen Ruihong,et al. The detection of weak physiological electric signals in strong background noise[J]. Journal of Huazhong University of Science and Technology,1994,22(9):119-123(in Chinese).
[12] 邵忍平,曹精明,李永龙. 基于 EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J]. 振动与冲击,2012,31(8):96-101,106.
Shao Renping,Cao Jingming,Li Yonglong. Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-nosing based on EMD [J]. Journal of Vibration and Shock,2012,31(8):96-101,106(in Chinese).
[13] Brincker R,Andersen P,Moller N B. An indicator for separation of structural and harmonic modes in outputonly modal testing[J]. Proceedings of the SPIE-The International Society for Optical Engineering,2000,2:1649-1654.
[14] 练继建,张建伟,李火坤,等. 泄洪激励下高拱坝模态参数识别研究[J]. 振动与冲击,2007,26(12):101-105.
Lian Jijian,Zhang Jianwei,Li Huokun,et al. Study on modal parameter identification of high arch dam under flood discharge excitation[J]. Journal of Vibration and Shock,2007,26(12):101-105(in Chinese).
(责任编辑:樊素英)
A Compound De-Noising Method for Operational Modal Identification of Offshore Wind Turbine Structure
Dong Xiaofeng,Lian Jijian,Yang Min,Wang Haijun
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
To solve the problem in identifying modal parameters accurately and retraining false modes induced by severe disruption due to the electromagnetic frequency signals,rotational frequency signals and environmental noise usually mixed in the acceleration data observed from prototype test of offshore wind turbine structure,a compound de-noising method,combining self-adaptive filter and ensemble empirical mode decomposition,was put forward to achieve filtering,noise reduction and modal identification for the first time. By means of testing signal processing in the new way including filtering,decomposing,de-noising and refactoring,much noise interference was reduced and full information of the structural vibration was reserved. Then the modal information will be identified preliminarily using both random decrement technique and eigensystem realization algorithm,and the false modes were eliminated by vibration mode analysis in order to obtain the operation modal parameters of offshore wind power structure correctly. Besides,the method presented here not only shows better accuracy and higher efficiency in noise reduction compared to the classic approaches which are lack of the statistical characteristics of noise,but also provides operational modal identification of wind turbine structure with a preferable applied value in engineering based on measured signals.
offshore wind power;modal identification;self-adaptive filtering;ensemble empirical mode decomposition(EEMD);mode shape analysis
TK8
A
0493-2137(2015)03-0203-06
10.11784/tdxbz201309047
2013-09-14;
2014-05-15.
国家高技术研究发展计划(863计划)资助项目(2012AA051702);国家创新研究群体科学基金资助项目(51021004);天津市应用基础及前沿技术研究计划(青年基金项目)资助项目(12JCQNJC04000).
董霄峰(1986— ),男,博士研究生,leovikkie@126.com.
练继建,tju_luntan@126.com.
