水电站泄流诱发厂房结构振动响应预测
2015-05-16徐国宾韩文文王海军章环境
徐国宾,韩文文,王海军,章环境
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
水电站泄流诱发厂房结构振动响应预测
徐国宾,韩文文,王海军,章环境
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
水流强烈紊动能够诱发水工建筑物的振动破坏.为尽可能减小失事危险,确保大坝安全运行,寻求某种方法利用较少的实测数据全面掌握水电站的振动状况成为关键.分别将粒子群优化(PSO)算法、遗传算法(GA)和果蝇优化算法(FOA)与径向基(RBF)神经网络相结合,来优化RBF扩展参数.根据某水电站泄洪表孔、排沙孔泄流时的现场实测数据,运用主成分分析法选择对厂房结构振动影响程度较大的足够多且不多余的关键因子构建神经网络,来预测厂房结构在其他未知工况下的振动情况.结果表明:PSO-RBF、GA-RBF和FOA-RBF这3种方法预测效果均良好,适合运用于泄流诱发水电站厂房结构振动响应的预测研究中,其中 FOA-RBF方法的稳定性及泛化能力最强,可为其他类型电站的振动研究提供参考.
水电站;厂房振动;粒子群优化(PSO)算法;遗传算法(GA);果蝇优化算法(FOA);径向基(RBF)神经网络;主成分分析
当宣泄洪水时,紊动水流流经泄洪建筑物时容易引起水工建筑物的振动,即流激振动.水流诱发振动是一种极其复杂的流体与结构相互作用的现象.国内外对于流激振动引起的安全事故屡有报道,比如:美国得克萨斯州 Texar-Kana Dam、加利福尼亚州Trinky Dam、新泽西州Navaio Dam消力池导墙的破坏,马尔巴索工程溢洪道的破坏[1],前苏联伏尔加水电站拦鱼墩倒塌,贵州山坳拱坝溢流时强烈振动和万安水利枢纽溢洪道导墙倒塌等,均是由水流诱发振动所导致.
早在20世纪30年代,人们就注意到了水流诱发振动的危害性并开始进行研究.随着水利工程高水头、大流量、高流速泄水建筑物的大量兴建,特别是由于高强建筑材料的开发与应用,工程结构越来越趋于轻型化,水流诱发振动问题将更加突出.为尽可能减小失事危险,确保大坝安全运行,寻求某种方法利用较少的实测数据达到全面掌握水电站振动状况成为新的研究课题.
本文将粒子群优化(particle swarm optimization,PSO)算法、遗传算法(genetic algorithm,GA)以及果蝇优化算法(fruit flies optimization algorithm,FOA)分别与径向基(radial basis function,RBF)神经网络相结合,达到优化 RBF神经网络扩展参数 P的目的.结合某水电站泄洪表孔、排沙孔泄流时尾水紊动会引起的厂房结构振动这一现象,得到相关的实测数据.在所有的泄流引起的脉动压力及振动等众多影响因子中,依据主成分分析(principal component analysis,PCA)的基本思想,选择出对厂房结构振动影响程度较大的足够多但不多余的关键因子,构建 PSORBF、GA-RBF、FOA-RBF 3种优化方法,分别来预测厂房结构在其他未知工况下的振动情况.
1 智能算法优化RBF神经网络
RBF神经网络是一种基于非线性回归理论的神经网络,结构简单、训练速度快,具有很强的非线性映射能力,在函数逼近和学习速度上有较强的优势,适用于解决各种非线性问题,被广泛应用于各工程领域[2].
在MATLAB中,通过调用newrbe函数可以生成一个RBF神经网络,格式为
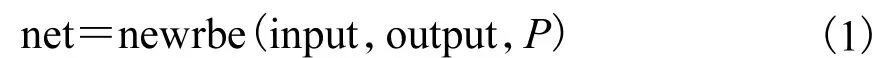
式中:input、output分别为输入和输出样本向量;P为扩展参数,即响应宽度.
P越大,函数的拟合越平滑,但是,过大的 P意味着需要非常多的神经元以适应函数的变化,会导致网络中神经元响应区域过度交叠,造成网络的欠适性;P过小,则会导致网络中神经元响应区域不能覆盖整个输入范围,造成网络的不适性.因此,如何选择扩展参数P,直接关系到神经网络性能的好坏.
1.1 PSO算法
PSO算法是一种模拟鸟类相互协作寻找食物的智能算法[3],通过粒子间的竞争和协作达到实现在复杂搜索空间中寻找全局最优点的目的.它不仅具有易理解、易实现以及很强的全局寻优能力,而且可以通过设定参数来提高网络的局部寻优能力,搜索思维和种群之间经验共享方式更加科学,在大多数情况下,能更快地寻找到最优解[4].
PSO算法基本原理:将每个个体看作 D维搜索空间的一个没有体积的粒子,由 m个微粒组成的微粒群在搜索空间中以一定的速度v飞行,粒子的飞行速度由它本身的飞行经验以及同伴的飞行经验进行动态调整.第i个微粒的当前位置为Xi,将Xi作为优化问题的潜在解代入优化目标函数中,计算出相应的适应度值,根据适应度值大小衡量微粒的优劣,并记录所经历的历史最好位置 Gi.微粒 i的飞行由式(2)、式(3)决定.
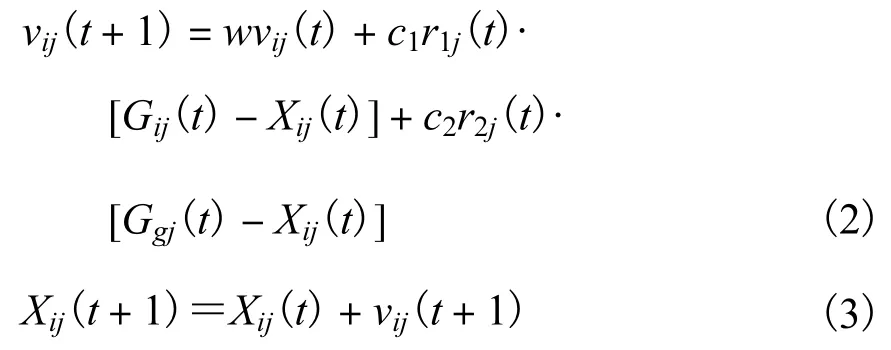
式中:w为惯性权重;下标j表示微粒的j维;下标i表示第i个微粒;t表示进化到第t代;c1、c2为加速常数;r1、r2是在[0,1]范围内变化的随机数.
PSO-RBF是PSO算法与RBF神经网络的结合,该方法以 RBF神经网络的均方差作为适应度函数,运用粒子群优化算法对RBF神经网络中的扩展参数P进行优化选择.该方法在无线传感器网络入侵检测技术研究[5]、大坝变形监测[6]、模拟电路诊断[7]、系统辨识方法仿真[8]等各个方面得到了广泛应用,但在厂房结构振动响应预测中还较少有应用.
1.2 GA
GA属于进化算法的一种,它通过模仿自然界选择与遗传的机理来寻找最优解,是从生物遗传、进化的过程得到启发而提出的.算法中称遗传的生物体为个体,个体对环境的适应程度用适应值表示.适应值取决于个体的染色体,在算法中染色体常用一串数字表示,数字串中的一位对应一个基因.一定数量的个体组成一个群体.对所有个体进行选择、交叉和变异等操作,生成新的群体.
GA-RBF是GA与RBF神经网络的结合,经过对算子的选择、交叉和变异等操作,充分利用遗传算法收敛性好、计算时间少、鲁棒性高等优点,选择出RBF神经网络所需要的最优秀的算子.此方法被广泛应用于各个领域[9-12].
1.3 FOA
FOA是一种基于果蝇觅食行为推演出寻求全局优化的新方法,由中国台湾学者潘文超[13]2011年提出,用于金融预警模型研究中[14].FOA有很好的群体智能性,其应用领域相当广泛,特别是在函数优化、神经网络、支持向量回归参数优化、财务管理、企业风险预警方面有着重要的应用价值.
FOA采用距离、位置搜索方法.先按照式(4)估算粒子与原点之间的距离 Di;再按照式(5)计算适应度判定值 Si;然后将 Si代入适应度判定函数式(6)中,求出该果蝇个体位置的适应度;最终根据式(7),通过不断地迭代寻优,找出此果蝇群体中适应度最佳的果蝇.
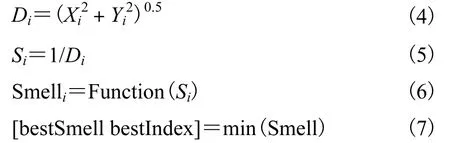
FOA-RBF是基于 FOA的 RBF神经网络,把FOA中的适应度判定值 Si看作 RBF神经网络的扩展参数值,利用FOA对RBF神经网络进行寻优,选用神经网络的均方差作为适应度判定函数,快速准确地找到最佳扩展参数,以便准确建立预测模型,达到良好的预测效果.FOA-RBF具体优化过程及MATLAB伪代码如下.
(1) 设置计算参数并初始化果蝇群体位置.
maxgen=20%迭代次数
sizep=40%种群规模
X_axis=rand(·)
Y_axis=rand(·)
(2) 随机设置果蝇飞行方向与距离,即利用果蝇的嗅觉搜寻食物的随机方向与距离.
Xi=X_axis+20rand(·)-10
Yi=Y_axis+20rand(·)-10
(3) 通过式(4)、(5)求出适应度判定值Si.
(4) 将学习样本和适应度判定值Si代入newrbe函数,计算适应度值Functioni.
net=newrbe(input,output,Si)%网络模型建立
yc=sim(net,input2)%神经网络仿真
y=yc-output2%网络输出与目标值误差
Functioni=mse(y)%预测误差的均方值
(5) 比较第 i个粒子所经过的所有位置的适应度值,确定其最优位置.
[bestSmell,bestIndex]=min(Function)
If bestFunction<Functionbest
X_axis=X(bestIndex)
Y_axis=Y(bestIndex)
bestS=S(bestIndex)
Functionbest=bestFunction;end
(6) 保留最佳值位置与最佳适应度值,并纪录每代最优值到yy数组中.
yy(gen)=Functionbest
Xbest(gen)=X_axis
Ybest(gen)=Y_axis
(7) 果蝇迭代寻优,重复执行步骤(2)~(5),并判断适应度值是否优于前一迭代,若是则执行(6).
(8) 达到迭代终止条件,搜索到适应度最佳的果蝇,得到最佳适应度值.
2 实例仿真分析
2.1 样本选取
为了对泄流引起的水电站厂房结构振动响应进行预测分析,现以某厂顶溢流式水电站排沙孔全开,机组暂停运行,表孔由关闭到完全开启共计 12种工况(见表 1)的实测数据为依据.选取该水电站泄流表孔上游侧盖板上游侧测点 A、下游侧盖板上游侧测点B、坝体泄流表孔中线 0+42.7测点 C、0+60.2测点D共计 4处不同压力水头、水压脉动 100%双幅值、标准差等 12个影响因子的实测数据作为输入数据(见表2);相应A、B两处厂坝结构测点的x、z径向振动位移实测值作为输出数据(见表3).
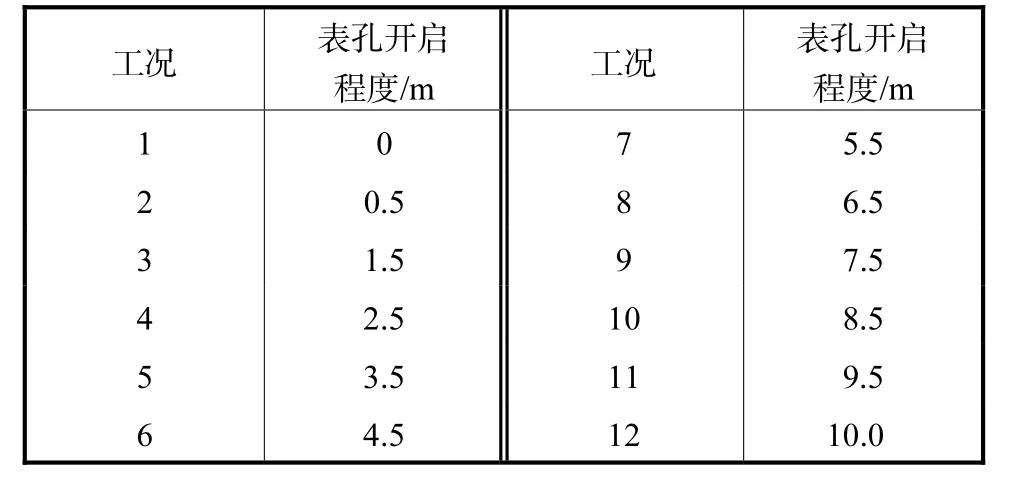
表1 12种工况下的表孔开启程度Tab.1 Surface outlet under twelve kinds of working conditions
2.2 主成分分析
利用神经网络进行预测时,若输入因子少,导致其预测准确性低;若输入因子多,则神经网络运算量大,导致其预测结果得不到收敛.主成分分析法可以将多个变量通过线性变换以选出较少个数重要因子的一种多元统计分析方法,又称主分量分析.
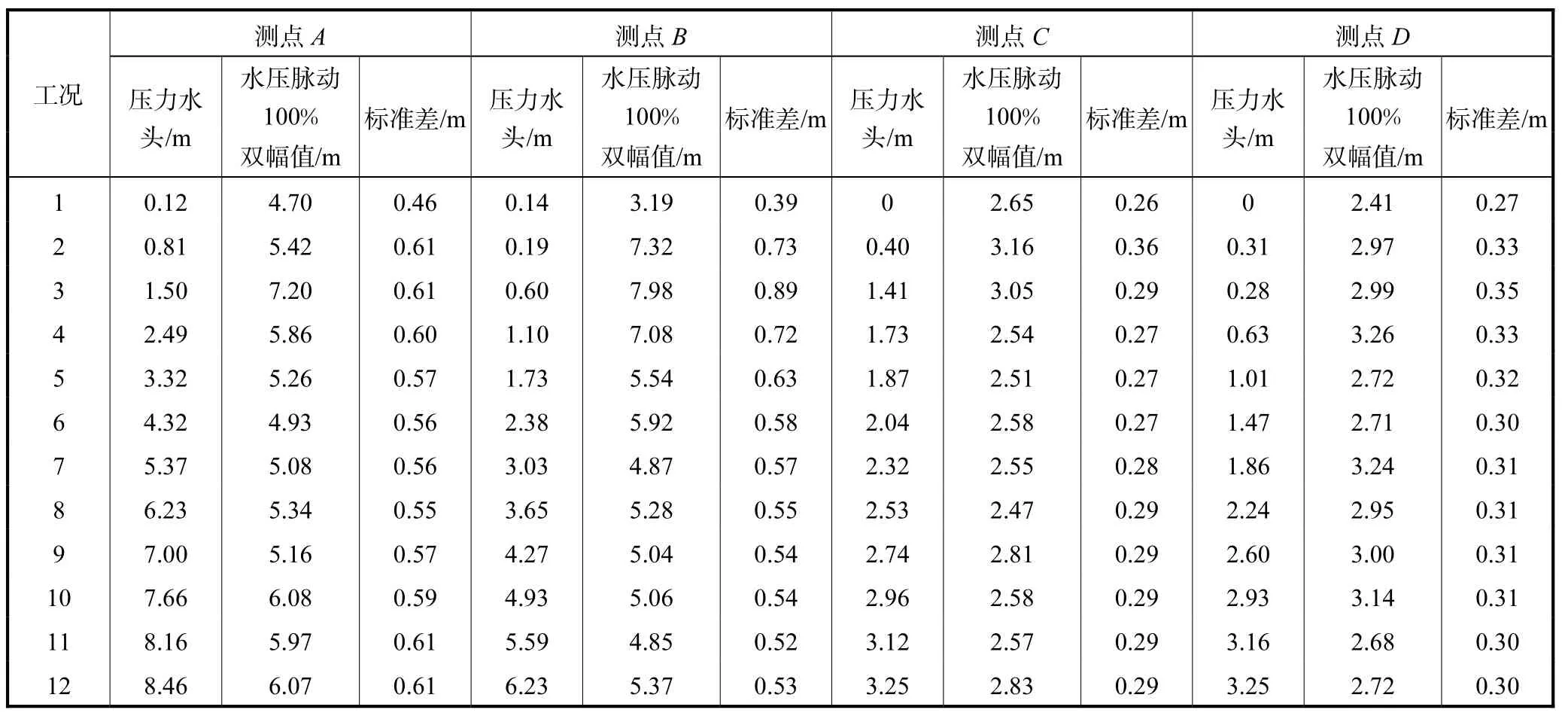
表2 输入数据Tab.2 Input data
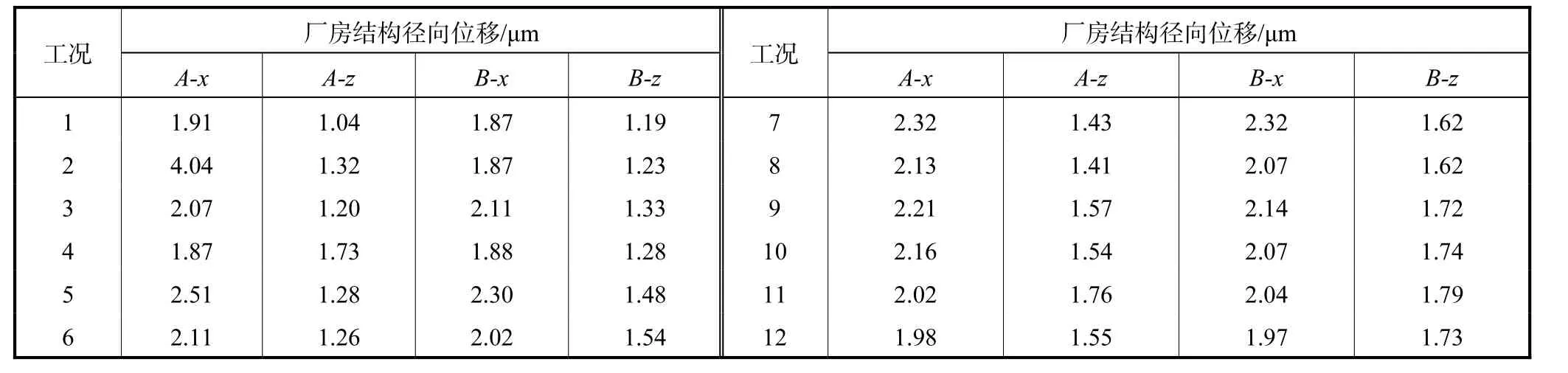
表3 输出数据Tab.3 Output data
在统计分析软件 SPSS中,运用 PCA法将影响因子进行简化处理,可以选择出适当的影响因子,有助于提高预测精度.具体步骤为:①对表 2中测点A、B、C、D处压力水头、水压脉动100%双幅值、标准差等 12个影响因子进行标准化处理;②利用标准化后的数据计算影响因子相关系数矩阵;③计算相关系数矩阵特征值和特征向量;④计算每个成分的贡献率以及前N个主成分累积贡献率.
主成分分析结果表明,表2中前10个影响因子的累积贡献率达到 100%,足以涵盖建立模型需要的信息,且不多余.于是在神经网络的创建、训练以及测试中,选用前 10种因子的实测数据作为输入数据.为了对主成分评价的效果进行比较,证明其有效性,分别选取前 4种因子(影响因子个数 N=4)和全部因子(N=12)作为输入数据进行对比测试.
依据某灯泡贯流式机组、厂顶溢流式水电站的原型观测数据,分别应用 PSO-RBF、GA-RBF、FOARBF、RBF(扩展参数采用默认值,即 P=1)神经网络建立预测模型,对水电站振动响应问题展开研究.
2.3 模型的创建与训练
将所有的样本数据分为测试部分和训练部分,训练数据用来进行模型的创建和训练,测试数据进行仿真预测以及误差分析.随机选取工况 11、12作为测试数据,其余10种工况作为训练数据.
PSO-RBF初始参数设置:粒子群个数 sizep为40;最大迭代次数 maxgen为 20;学习因子 c1=c2=1.494,45;惯性权重 w=0.729;粒子群初始取值范围[-10,10],种群限制 Xi∈[-10,10];速度限制 vi∈[-1,1].
GA-RBF初始参数设置:粒子群个数 sizep设为40;最大迭代次数maxgen为10;杂交概率设定为pc为 0.6;变异概率取值为 pm=0.001-[1∶1∶sizep]·(0.001)/sizep等.
FOA-RBF初始参数设置:粒子群个数 sizep为40;最大迭代次数maxgen为20.
2.4 模型的测试效果分析
将测试数据代入已经训练好的预测模型中进行振动响应仿真测试.分别对 PSO-RBF、GA-RBF与FOA-RBF这3种方法进行了30次测试,每次测试得到的最佳适应度值如图1~3所示.
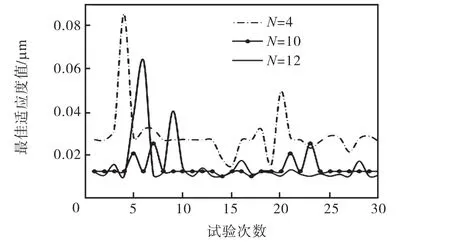
图1 PSO-RBF 30次测试最佳适应度值Fig.1 30 times best fitness values of PSO-RBF
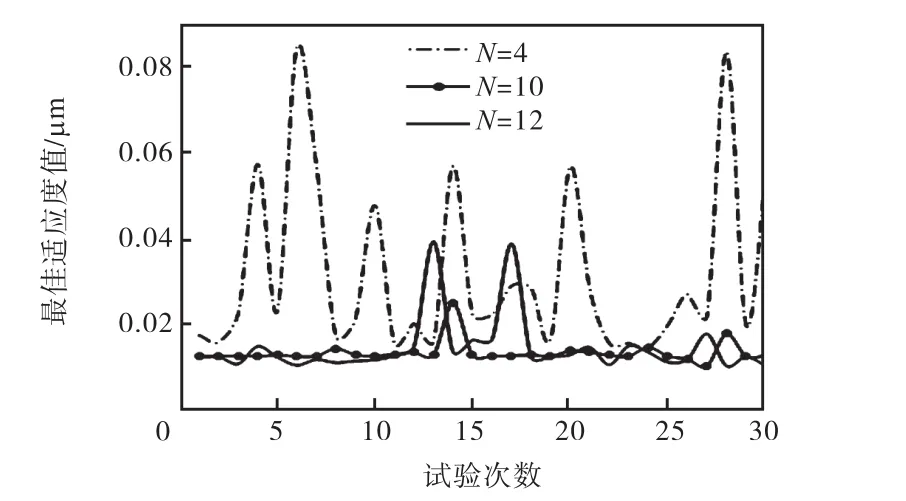
图2 GA-RBF 30次测试最佳适应度值Fig.2 30 times best fitness values of GA-RBF
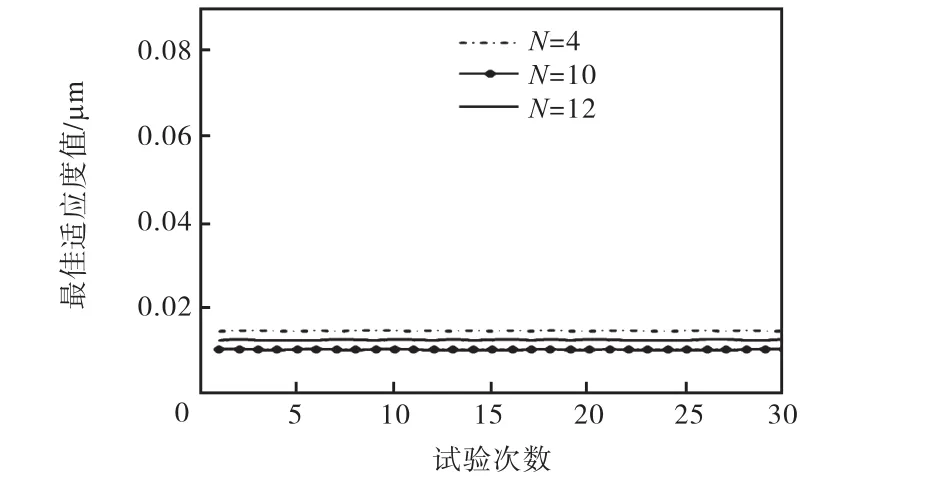
图3 FOA-RBF 30次测试最佳适应度值Fig.3 30 times best fitness values of FOA-RBF
分别观察图 1~3可知,影响因子个数 N=10时,每种方法、每次测试所得的最佳适应度值在一个相对更小、更稳定的范围内变化,说明影响因子个数N=10时建立的模型的稳定性及预测效果比 N=4、N=12都好.
比较图 1~图 3可以看出,与其他两种方法相比,FOA-RBF的预测结果不仅适应度更优,而且波动较小,稳定性更好.
表4统计了30次测试结果的平均值、最优值和最差值.由此可以进一步看出,无论是最优值、最差值还是平均值,在N=10时,预测效果明显优于N=4和 N=12.这说明了主成分分析的有效性,为以后水电站实测数据的处理提供了新思路.
下面就影响因子个数N=10时不同模型的预测效果进行详细分析.
由表 4可知,在给定的迭代步骤内,PSO-RBF、GA-RBF与FOA-RBF 3种方法得到的最佳适应度的平均值分别为 0.014,2、0.013,7和 0.010,7,与一般RBF神经网络所得结果0.035,1相比均处于一个更低的水平,说明这3种方法在厂房结构振动响应预测中都比较适用.

表4 预测结果统计Tab.4 Statistical prediction results
PSO-RBF、GA-RBF和FOA-RBF 3种方法得到的实测值与预测值对比如表 5和表 6所示.PSORBF、GA-RBF和FOA-RBF 3种方法的相对误差均控制在较低水平,而一般的 RBF神经网络最大相对误差达到 18.260%,与实际情况相差太大.这再次说明3种方法对扩展参数P的优化均达到了很好的效果,大大提高了RBF神经网络的预测性能.
3种方法中,FOA-RBF除工况11下A-z测点预测值与实测值相差较大外,其他2种方法的预测值与实测值的相对误差都控制在 5%以内,而且误差的均方值最小,说明其泛化能力更强.
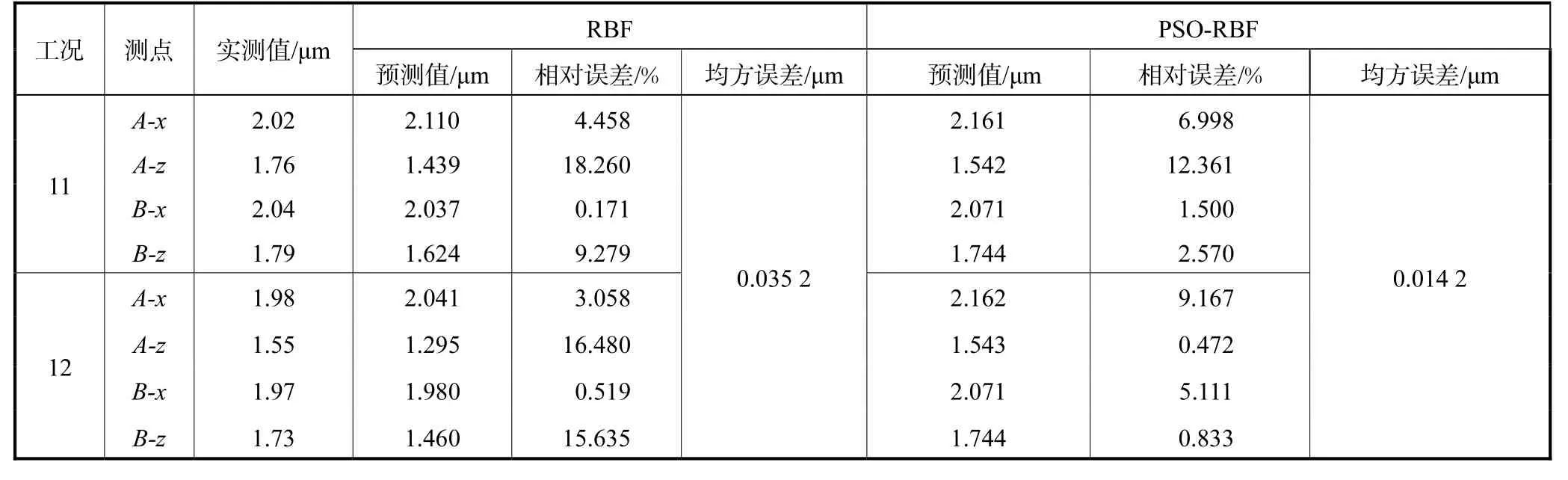
表5 实测值与预测值比较(RBF和PSO-RBF)Tab.5 Comparison between measured and predicted values(RBF and PSO-RBF)
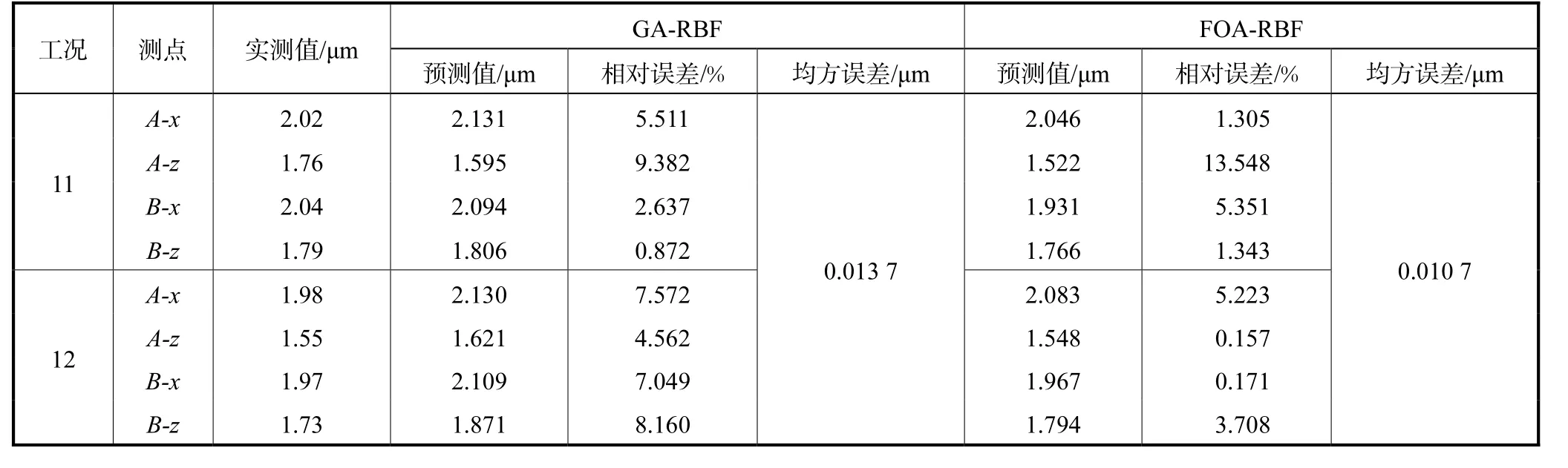
表6 实测值与预测值比较(GA-RBF和FOA-RBF)Tab.6 Comparison between measured and predicted values(GA-RBF and FOA-RBF)
3 结 论
(1) 运用粒子群优化(PSO)算法、遗传算法(GA)和果蝇优化算法(FOA)优化径向基(RBF)神经网络,实现了智能算法与神经网络的结合.在泄流引起的厂房结构振动响应预测研究中,PSO-RBF、GARBF和FOA-RBF这3种方法的预测效果均良好,说明这 3种方法都能够运用在水电站结构振动响应预测研究中.可为其他类型的水电站原型观测资料处理提供一个新方法,为增强厂房振动智能化监测提供保障.
(2) 依据主成分分析的基本思想,在所有的泄流引起的脉动压力及振动位移等众多影响因子中,选择出对厂房结构振动影响程度较大的足够多且不多余的关键因子,用这些因子建立的模型的预测精度得到了提高.说明了主成分分析的有效性,为以后水电站实测数据的处理提供了新思路.
(3) FOA原理简单,易于学习和应用;需要调节的参数少,受人为因素影响更小.FOA-RBF能够更准确地选择适合的扩展参数 P,更好地建立预测模型,大大降低了预测误差.
[1] 刘沛清,刘心爱,李福田. 消力池底板块的失稳破坏机理及其防护措施[J]. 水利学报,2001(9):1-9.
Liu Peiqing,Liu Xin′ai,Li Futian. Failure mechanism of bottom plate in stilling basin and countermeasure for protection[J]. Journal of Hydraulic Engineering,2001(9):1-9(in Chinese).
[2] 韩力群. 人工神经网络[M]. 北京:北京邮电大学出版社,2006:127-139.
Han Liqun. The Artificial Neural Network[M]. Beijing:Beijing University of Posts and Telecommunications Press,2006:127-139(in Chinese).
[3] Kennedy J,Eberhart R. Particle swarm optimization [C]//Proceedings of IEEE International Conference on Neural Networks. Perth,Australia,1995:1942-1948.
[4] 张顶学,关治洪,刘新芝. 基于 PSO的RBF神经网络学习算法及其应用[J]. 计算机工程与应用,2006(20):13-15.
Zhang Dingxue,Guan Zhihong,Liu Xinzhi. RBF neural network algorithm based on PSO algorithm and its application[J]. Computer Engineering and Applications,2006(20):13-15(in Chinese).
[5] 易晓梅,吴 鹏,刘丽娟,等. 基于 PSO-RBF无线传感器网络入侵检测技术研究[J]. 传感器与微系统,2011,30(9):9-11.
Yi Xiaomei,Wu Peng,Liu Lijuan,et al. Research on WSNs intrusion detection technology based on PSORBF[J]. Transducer and Microsystem Technologies,2011,30(9):9-11(in Chinese).
[6] 吕蓓蓓,杨远斐. PSO-RBF在大坝变形监测中的应用[J]. 水电能源科学,2012,30(8):77-79.
Lü Beibei,Yang Yuanfei. Application of PSO-RBF in dam deformation monitoring[J]. Water Resources and Power,2012,30(8):77-79(in Chinese).
[7] 宋丽伟,彭敏放,田成来,等. 基于 PSO-RBF 神经网络的模拟电路诊断[J]. 计算机应用研究,2012,29(1):72-74.
Song Liwei,Peng Minfang,Tian Chenglai,et al. Analog circuit diagnosis based on particle swarm optimization radial basis function network[J]. Application Research of Computers,2012,29(1):72-74(in Chinese).
[8] 丁宏锴,萧蕴诗,李斌宇,等. 基于 PSO-RBFNN的非线性系统辨识方法仿真研究[J]. 系统仿真学报,2005,17(8):1826-1829.
Ding Hongkai,Xiao Yunshi,Li Binyu,et al. Study on simulation of nonlinear system identification based on PSO-RBFNN[J]. Acta Simulata Systematica Sinica,2005,17(8):1826-1829(in Chinese).
[9] 周佩玲,陶小丽,傅忠谦,等. 基于GA的RBF网络用于旱涝灾害因素预测研究[J]. 计算机应用,2001, 21(1):7-9.
Zhou Peiling,Tao Xiaoli,Fu Zhongqian,et al. Disaster elements prediction with RBF network based on GA [J]. Computer Applications,2001,21(1):7-9 (in Chinese).
[10] 刘国海,蒋志佳. 基于GA-RBF和不变矩的高压瓷瓶裂缝识别[J]. 控制工程,2009,16(5):561-565.
Liu Guohai,Jiang Zhijia. Recognition of porcelain bottle crack based on GA-RBF and moment invariants[J]. Control Engineering of China,2009,16(5):561-565(in Chinese).
[11] 王 峰,谈怀江. GA-BP和GA-RBF网络在结构损伤分析的比较[J]. 微机发展,2005,15(8):158-160.
Wang Feng,Tan Huaijiang. Comparison between GABP and GA-RBF neural network applying to analysis of structural damage[J]. Microcomputer Development,2005,15(8):158-160(in Chinese).
[12] 郑丕谔,马艳华. 基于 RBF 神经网络的股市建模与预测[J]. 天津大学学报,2000,33(4):483-486.
Zheng Pi′e,Ma Yanhua. RBF neural network based stocks market modeling and forecasting[J] Journal of Tianjin University,2000,33(4):483-486(in Chinese).
[13] 潘文超. 果蝇最佳化演算法[M]. 台湾:沧海书局,2011.
Pan Wenchao. Flies Optimization Algorithm[M]. Taiwan:Canghai Publishing House,2011(in Chinese).
[14] Pan W T. A new evolutionary computation approach:Fruit fly optimization algorithm[C/OL] //2011 Conference of Digital Technology and Innovation Management. Taipei,China,2011:http://www.oitecshopbyethost 16. com/ FOA. html.
(责任编辑:樊素英)
Prediction of Vibration Response of Powerhouse Structures Caused by Flow Discharge
Xu Guobin,Han Wenwen,Wang Haijun,Zhang Huanjing
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Strong flow turbulence may cause vibration fracture of hydraulic structures. To minimize risks and ensure safe operation of dam,it is essential to search for some methods and use fewer monitoring data to achieve comprehensive grasp of powerhouse vibration conditions. Combining particle swarm optimization(PSO)algorithm,genetic algorithm(GA)and fruit flies optimization algorithm(FOA)with radial basis function(RBF) neural networkrespectively,the spreading parameter of RBF was optimized. Based on monitoring data of structure vibration under the condition of surface outlet and sediment outlet discharge,and adopting principal component analysis method,adequate but not redundant influence factors were selected. Neural network was built to predict vibration of other unknown conditions. Results show that PSO-RBF,GA-RBF and FOA-RBF methods are appropriate for prediction research of vibration response of powerhouse structures caused by flow discharge. FOA-RBF is the most stableof the three methods,providing a reference for other power station vibration research.
hydropower station;vibration of powerhouse;particle swarm optimization(PSO)algorithm;genetic algorithm(GA);fruit flies optimization algorithm(FOA);radial basis function(RBF)neural network;principal component analysis(PCA)
TV312;TV731
A
0493-2137(2015)03-0196-07
10.11784/tdxbz201308072
2013-08-29;
2013-09-30.
国家创新研究群体科学基金资助项目(51321065).
徐国宾(1956— ),男,教授.
徐国宾,xuguob@sina.com.
时间:2013-11-08.
http://www.cnki.net/kcms/detail/12.1127.N.20131108.1542.009.html.
