TOPAZ-Ⅱ反应堆135Xe小反应性计算方法研究
2015-05-16安伟健赵守智刘兴民吴晓春
安伟健,赵守智,沈 峰,孙 征,刘兴民,吴晓春
(1.中国原子能科学研究院反应堆工程研究设计所,北京 102413;2.国家核电技术有限公司北京软件技术中心,北京 100029)
TOPAZ-Ⅱ反应堆135Xe小反应性计算方法研究
安伟健1,赵守智1,沈 峰2,孙 征1,刘兴民1,吴晓春1
(1.中国原子能科学研究院反应堆工程研究设计所,北京 102413;2.国家核电技术有限公司北京软件技术中心,北京 100029)
TOPAZ-Ⅱ反应堆的中子通量密度很低,这使其在运行过程中引入的135Xe反应性很小,其数值难以采用现有的蒙特卡罗程序进行计算。本文考虑了中子价值对反应性的作用,采用MVP-BURN程序对TOPAZ-Ⅱ反应堆的135Xe小反应性进行了计算。该方法可为其他类似反应堆的小反应性计算提供参考。
TOPAZ-Ⅱ;135Xe小反应性;MVP-BURN程序;中子价值
TOPAZ-Ⅱ反应堆是俄罗斯CDBMB、Kurchatov及Lutch等研究机构联合开发的空间热离子核反应堆,是目前世界上最先进的空间核反应堆之一。135Xe反应性的计算是反应堆核设计的重要内容,其数据是反应堆控制的必要输入参数。对于一般的热中子反应堆,135Xe的反应性数值较大,可分别通过计算系统在含和不含135Xe时的Δkeff来得到。但对于TOPAZ-Ⅱ反应堆,由于其中子通量密度很低,使其135Xe反应性的数值很小,与蒙特卡罗程序输出的keff统计误差的数量级相同,因此难以通过计算Δkeff而得到准确的数值。本文通过对中子价值的充分考虑,采用MVP-BURN程序对TOPAZ-Ⅱ反应堆的135Xe小反应性进行计算。
1 TOPAZ-Ⅱ反应堆堆芯描述
TOPAZ-Ⅱ反应堆(图1)主要由37根热离子燃料元件、氢化锆慢化剂、不锈钢堆芯筒体、铍反射层、12个转鼓及其他一些堆内构件组成。TOPAZ-Ⅱ反应堆的基本参数列于表1。
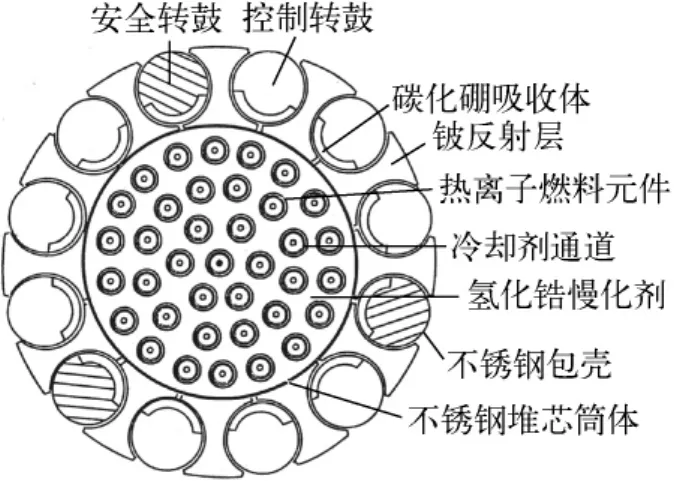
图1 TOPAZ-Ⅱ反应堆结构Fig.1 Structure of TOPAZ-Ⅱreactor

表1 TOPAZ-Ⅱ反应堆的基本参数[1]Table 1 Basic parameters of TOPAZ-Ⅱreactor[1]
2 计算程序及模型
本文采用日本原子力研究所开发的带燃耗计算功能的蒙特卡罗程序MVP-BURN[2],根据TOPAZ-Ⅱ反应堆的对称性建立一1/24堆芯模型(径向1/12,轴向1/2),如图2所示。

图2 TOPAZ-Ⅱ1/24堆芯轴向和径向结构示意图Fig.2 Axial and radial views of TOPAZ-Ⅱ1/24 reactor core
在各对称交界面分别采用镜反射边界条件,临界计算得到冷态工况下的keff为0.999 6,与MCNP临界计算的结果1.004 3相比,相对偏差在0.5%以内,可认为此模型是准确、可信的。
3 问题的提出
采用MVP-BURN程序计算Δkeff的方法计算寿期初135Xe的反应性,每次临界计算运行2 000代,忽略最初的50代,每代跟踪的中子数为10 000个。经计算得到此时的keff统计误差约为1.7×10-4,该数值与135Xe反应性的数量级相同。图3为计算得到的寿期初135Xe的反应性,可看出,135Xe反应性随时间的变化是杂乱无章的,不能反映真实的135Xe反应性引入过程。
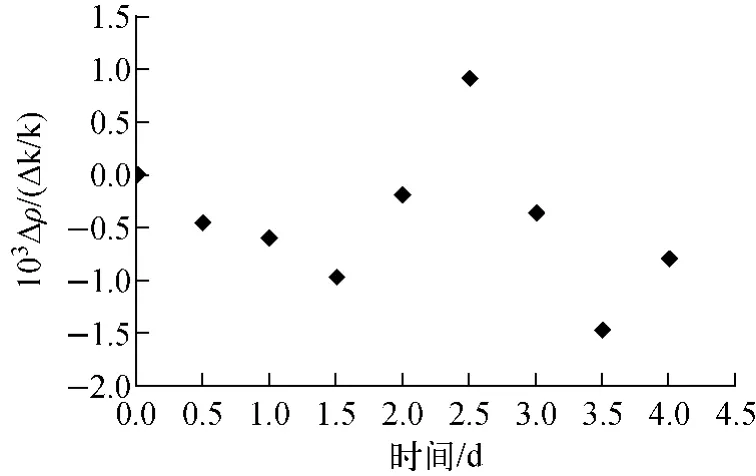
图3 寿期初135Xe反应性的计算结果Fig.3 Calculated135Xe reactivity at beginning of life
4 计算方法的探索
为能准确地计算TOPAZ-Ⅱ反应堆的135Xe小反应性,本工作尝试3种计算方法。为检验这些计算方法的准确性,首先建立如下模型:在其他条件保持不变的情况下,假设将TOPAZ-Ⅱ反应堆的功率提升至原来的72倍,即8.28 MW,这会使135Xe反应性大幅增加,远大于keff的统计误差,从而可通过计算Δkeff来获得较准确的结果,如图4所示。以下以此作为参考结果来检验3种方法的准确性。

图4 通过计算Δkeff得到的8.28 MW工况下寿期初135Xe的反应性Fig.4135Xe reactivity calculated byΔkeffat beginning of life under 8.28 MW power
4.1 方法1
TOPAZ-Ⅱ反应堆内135Xe吸收的中子超过99.9%是热中子(小于1 e V),根据四因子模型可认为,135Xe对系统反应性的影响主要体现在热中子利用系数f上[3],由此得到135Xe的反应性为:

式中:f′为系统不含135Xe时的热中子利用系数;ΣXea为燃料的宏观热中子吸收截面;Σa为系统中除135Xe以外的宏观热中子吸收截面。
由方法1计算得到的8.28 MW工况下寿期初135Xe的反应性如图5所示。
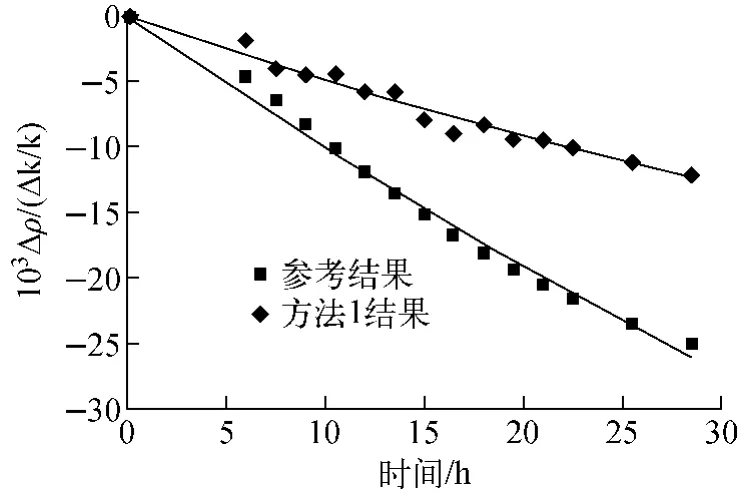
图5 方法1计算得到的8.28 MW工况下寿期初135Xe的反应性Fig.5135Xe reactivity calculated by method 1 at beginning of life under 8.28 MW power
由图5可看出,由方法1计算得到的结果与参考结果相差较大。分析其原因为:由于TOPAZ-Ⅱ反应堆的能谱属于超热谱,较一般热中子反应堆的能谱硬(TOPAZ-Ⅱ反应堆中由热中子引起的裂变仅占总裂变的47%),这使四因子模型对TOPAZ-Ⅱ反应堆的适用性较差。
4.2 方法2
由于TOPAZ-Ⅱ反应堆能谱较一般热中子反应堆硬,其不宜仅考虑热中子的作用,因此尝试在方法1的基础上,采用135Xe的总宏观吸收截面与系统的总宏观吸收截面的比值作为135Xe反应性的大小。由此得到8.28 MW工况下寿期初135Xe的反应性如图6所示。
由图6可看出,方法2计算得到的结果与参考结果仍有明显的差别,分析其原因为:方法2将135Xe吸收的中子数作为衡量其对系统影响的唯一因素,但实际上135Xe对系统的影响还与其吸收的中子价值(中子价值可理解为吸收1个中子所引起的系统反应性的损失)有关。TOPAZ-Ⅱ反应堆内135Xe吸收的中子超过99.9%是热中子,而堆芯吸收的中子仅约45%是热中子,因此,135Xe与堆芯所吸收的中子的平均能量并不相同。另外,135Xe吸收的中子均位于燃料内部,而堆芯吸收的部分中子位于燃料外面,因此,两者吸收中子的位置也不尽相同。对于系统的反应性来说,不同能量和不同位置的中子对系统反应性的贡献是不相同的,即135Xe吸收的中子与堆芯吸收的中子的价值是不同的,在评估135Xe反应性时应考虑中子价值的影响。
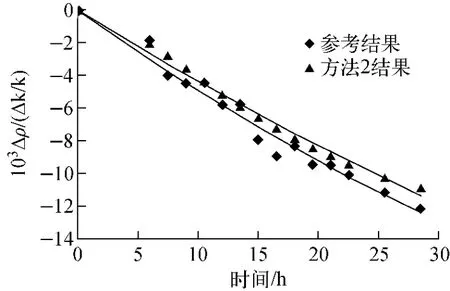
图6 方法2计算得到的8.28 MW工况下寿期初135Xe的反应性Fig.6135Xe reactivity calculated by method 2 at beginning of life under 8.28 MW power
4.3 方法3
从双群理论出发,由于TOPAZ-Ⅱ反应堆中超过一半的裂变反应是由快群中子引起,因此在双群方程中加入快群中子裂变项,则:
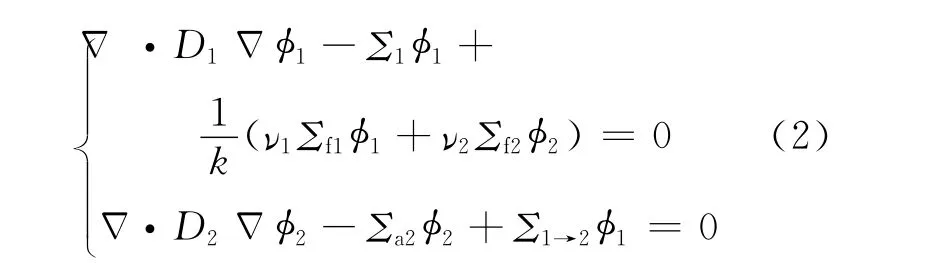
式中:D1、D2分别为快群中子和热群中子的扩散系数;φ1和φ2分别为快群中子和热群中子的通量密度;ν1和ν2分别为快群中子和热群中子的平均裂变中子数;Σf1和Σf2分别为快群中子和热群中子的宏观裂变截面;Σa2为热群中子的宏观吸收截面;Σ1为快群中子的宏观截面;Σ1→2为快群中子慢化为热群中子的宏观截面;k为系统的有效增殖因数。135Xe对系统的影响主要体现在Σa2和k上,则认为引入135Xe后:Σa2→Σa2+δΣa2,k→k+δk。由扰动方程[4]可得到135Xe反应性为:
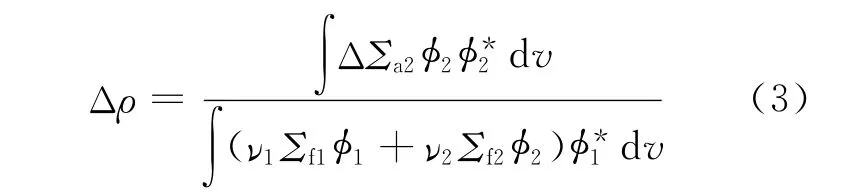


将式(4)代入式(3)可得:


图7中P0为燃料内热群中子的首次飞行逃脱概率,C为热群中子在碰撞时发生散射的概率。根据中子价值守恒原理,初始中子的价值应等于其所有后代中子价值的总和。图7中初始中子的后代中子可分为泄漏项和吸收项两部分,因此可建立如下关系式:
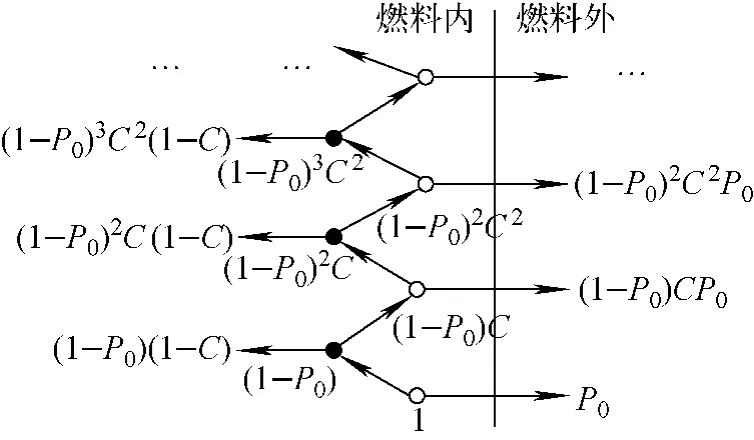
图7 燃料内的热群中子输运流程图Fig.7 Flow diagram of in-fuel thermal neutron



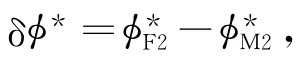

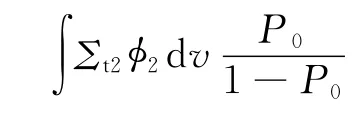
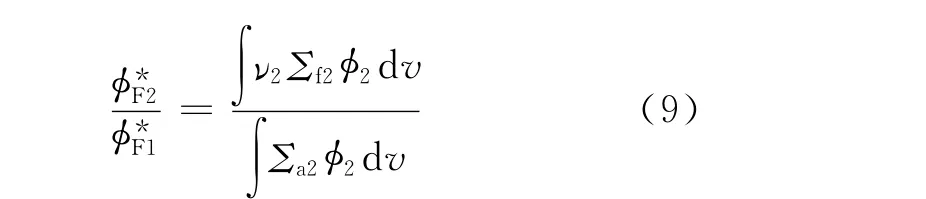
将式(9)代入式(5)可得:
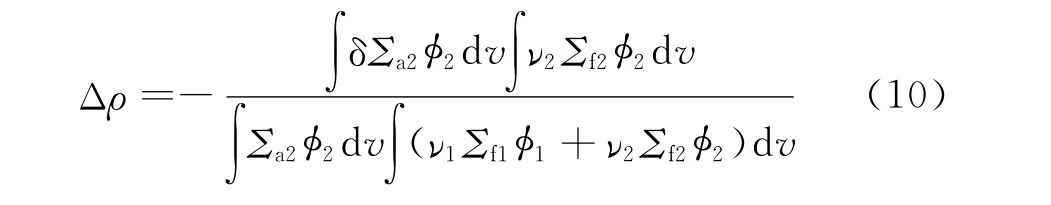
式(10)即是本工作建立的计算135Xe小反应性的公式,式中各积分项均可由MVPBURN程序计算得到。其中,∫δΣa2φ2d v为135Xe的热群中子吸收率;∫ν2Σf2φ2d v为燃料中由热群中子引起裂变得到的裂变中子产生率;∫Σa2φ2d v为燃料内热群中子的吸收率;∫(ν1Σf1φ1+ν2Σf2φ2)d v为燃料内总的裂变中子产生率。由方法3计算得到的8.28 MW工况下寿期初135Xe的反应性与参考结果符合较好,如图8所示。
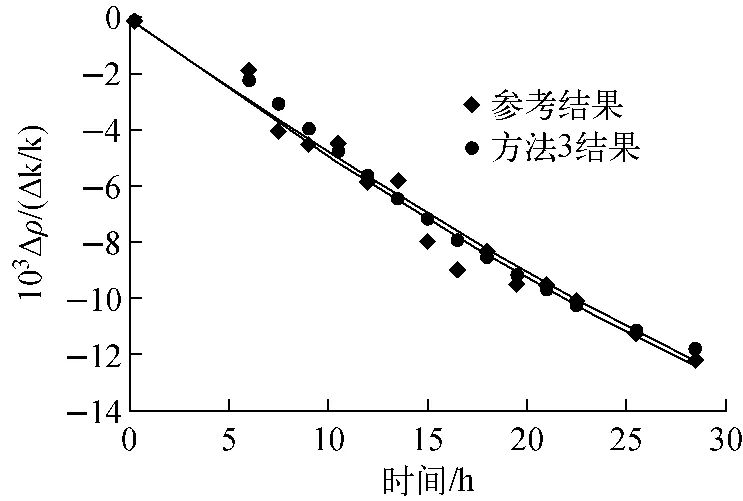
图8 方法3计算得到的8.28 MW工况下寿期初135Xe的反应性Fig.8135Xe reactivity calculated by method 3 at beginning of life under 8.28 MW power
5 计算结果
采用方法3计算得到的额定工况下的135Xe反应性,如图9所示。由图9可看出,额定工况下TOPAZ-Ⅱ反应堆的135Xe反应性在运行约4 d后达到平衡,较一般压水堆达到135Xe平衡的时间长得多,这主要是由于TOPAZ-Ⅱ反应堆的中子通量密度非常低所导致。135Xe反应性的平衡数值约为-3.0×10-4Δk/k。
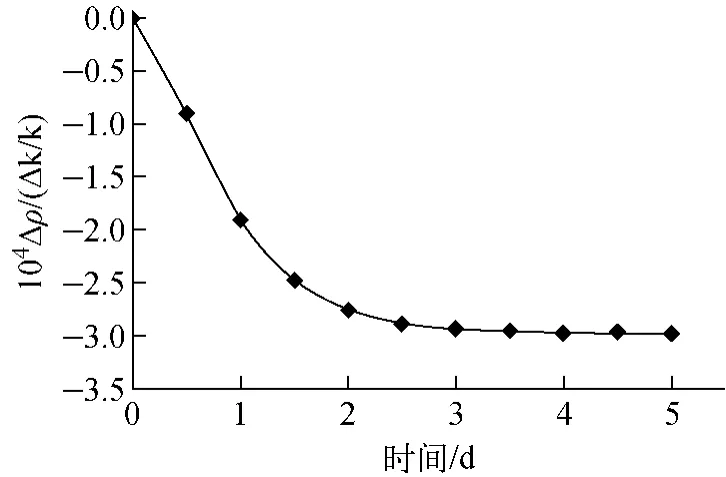
图9 由方法3得到额定工况下寿期初135Xe反应性引入过程Fig.9135Xe reactivity calculated by method 3 at beginning of life under rated power
为验证结果的准确性,采用计算Δkeff的方法来得到135Xe反应性的平衡数值:每次临界计算运行100 000代,忽略最初的100代,每代跟踪的中子数为10 000个,计算得到keff的统计误差约为3.0×10-5,135Xe的反应性为-3.3× 10-4Δk/k,由此可得出方法3的计算结果是合理可信的。对于各时间节点,方法3仅需进行1次临界计算,模拟运行2 000代;而计算Δkeff的方法需进行两次临界计算,每次模拟100 000代,因此无论在计算精度还是计算效率上,方法3均远优于计算Δkeff的方法。
6 结论
1)针对TOPAZ-Ⅱ反应堆的135Xe反应性太小而难以计算的问题,通过人为假设提升功率来增加135Xe的反应性,将其结果作为参考结果来检验3种方法的准确性,计算表明,方法3不仅可得到较准确的结果,而且其可大幅节省计算时间。
2)方法3充分考虑了中子价值对反应性的作用,本文通过推导,以更容易计算的反应率比值来替代中子价值的比值,这种推导方法可为其他涉及中子价值的问题提供参考。
[1] 解家春,赵守智,贾宝山,等.TOPAZ-Ⅱ反应堆慢化剂温度效应分析[J].原子能科学技术,2011,45(1):48-53.
XIE Jiachun,ZHAO Shouzhi,JIA Baoshan,et al.Analysis of moderator temperature effect for TOPAZ-Ⅱreactor[J].Atomic Energy Science and Technology,2011,45(1):48-53(in Chinese).
[2] OKUMURA K.MVP/GMVPⅡ:General purpose Monte Carlo codes for neutron and photon transport calculations based on continuous energy and multigroup methods[R].Japan:JAERI,2005.
[3] 谢仲生,尹邦华.核反应堆物理分析(上)[M].北京:原子能出版社,1994:218,253-254.
[4] 谢仲生,尹邦华.核反应堆物理分析(下)[M].北京:原子能出版社,1994:170-174.
[5] 陈仁济,阮可强.中子碰撞几率方法及其应用[M].北京:原子能出版社,1981:447-450.
Calculation Method of Small135Xe Reactivity for TOPAZ-ⅡReactor
AN Wei-jian1,ZHAO Shou-zhi1,SHEN Feng2,SUN Zheng1,
LIU Xing-min1,WU Xiao-chun1
(1.China Institute of Atomic Energy,P.O.Box 275-33,Beijing 102413,China;2.State Nuclear Power Software Development Center,Beijing 100029,China)
Due to the very low neutron flux density of TOPAZ-Ⅱreactor,the135Xe reactivity is too small for the Monte Carlo code to get the accurate results.In this paper,the adjoint neutron flux was taken into account,and the MVP-BURN code was used to calculate small135Xe reactivity.This method can also provide a reference for the calculation of small reactivity for other reactors.
TOPAZ-Ⅱ;small135Xe reactivity;MVP-BURN code;adjoint neutron flux
TL329
A
:1000-6931(2015)09-1637-05
10.7538/yzk.2015.49.09.1637
2014-05-05;
2014-10-29
安伟健(1987—),男,浙江台州人,硕士研究生,核能科学与工程专业
