LiCl溶液康普顿散射的影响因素研究

陈 凯，罗 光，曹红光，张丽鹏，陈 青，郭华清

（重庆师范大学物理与电子工程学院，重庆 400047）

LiCl溶液康普顿散射的影响因素研究

陈 凯，罗 光＊，曹红光，张丽鹏，陈 青，郭华清

（重庆师范大学物理与电子工程学院，重庆 400047）

基于康普顿散射理论对LiCl溶液康普顿散射中的非相干散射衰减因子进行了分析，采用一定近似处理得出了符合LiCl溶液康普顿散射相对光子数与浓度关系的表达式，并进行了实验验证。然后立足于密度泛函理论，从微观角度对LiCl溶液的康普顿散射进行了深入分析，得到了LiCl溶液中Li＋、Cl－的水合离子的电子结构，分析了电子数密度和电子受到的束缚对康普顿散射的影响。结果表明，除质量密度、散射衰减因子以及溶液的浓度对康普顿散射相对光子数有影响外，电子数密度和电子受到的束缚也对康普顿散射相对光子数有影响。

康普顿散射；等效电荷；电子数密度；溶液结构

康普顿散射［1］是物理学中非常重要的一种散射，在量子力学中一直占有非常重要的地位，已成为量子场论中研究电磁相互作用的一个典型例子［2－3］。与此同时，康普顿散射的应用研究一直是国内外的研究热点［4］，并已扩展到了天体物理、宇宙学以及高能物理领域［5－7］。

康普顿散射研究中，涉及散射体时，一般认为是固体散射体，如果换成液体甚至是溶液为散射体，如电解质溶液，由于分子、离子等的无规则热运动，溶液的结构处于动态平衡中，电解质在溶液中以游离态的离子、水分子、水合分子、低水合数的水合离子以及高水合数的离子存在，甚至阴阳离子互相进入对方的第一水合层，而形成的络合物也同样存在。因此研究上述结构对康普顿散射的影响，无疑是极有意义且必要的。基于此，本文选择LiCl溶液作为切入点以研究电解质溶液的康普顿散射。

1 理论

尽管液体和溶液的结构至今尚未被完全认识，但从宏观上看，液体和溶液的分布是均匀的，所以电子的分布从宏观上也是均匀的，体积元内发生的康普顿散射表现的也是一种平均效应，因此康普顿散射的相对光子数可反映电子数密度的平均效应。液体分子无规则的运动速度非常慢，相对于电子本身的运动速率（约为105m／s）可忽略。因此在研究康普顿散射时，可不考虑液体分子的无规则运动。入射光子的能量一般为几十eV至几MeV，相对于核的能量（质量）太小，光子与核的作用一般属于相干散射的范畴，因而可不予考虑。溶液浓度的改变将导致射线的质量衰减因子发生改变，致使入射方向的射线衰减因子f1x和散射方向的射线衰减因子f2x也发生变化。因为溶液浓度对入射衰减因子和散射衰减因子的影响是相同的，为更好地讨论这种影响，用衰减因子fx代替f1x和f2x，fx＝exp（－μd），其中，μ为非相干质量衰减因子，d为入（出）射光在散射体中经过的距离。文献［11］给出了LiCl溶液浓度的变化对衰减因子fx的影响，如表1所列，计算时将d假定为单位距离。

表1 射线衰减因子fx与LiCl溶液浓度x的关系Table 1 Relationship between attenuation factor fxand LiCl concentration x

由表1可知，射线衰减因子fx虽受浓度影响，但影响极小，甚至可忽略。如果使入射线和出射线对称，则f1x和f2x是相等的。

经过一定的近似处理，单位体积溶液的康普顿散射相对光子数与LiCl溶液浓度的关系最终可看作以下线性关系：

2 康普顿散射实验及结果

以137Cs为放射源（其能量为661．5keV，强度约为370MBq（10mCi））、LiCl为散射体溶液进行康普顿散射实验。实验装置示于图1。

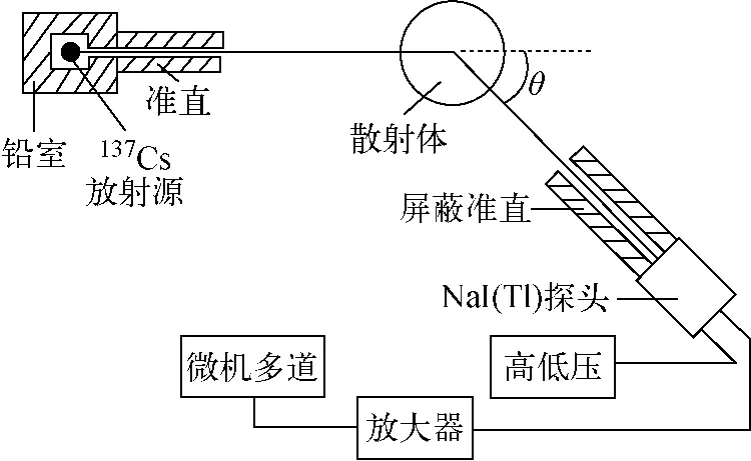
图1 实验装置示意图Fig．1 Schematic diagram of experimental apparatus

当散射角为40°和80°、采集时间为600s时，测定浓度分别为3．51%、7．02%、10．53%、14．05%、17．56%的LiCl溶液的康普顿散射相对光子数，对所得结果采用最小二乘法进行线性拟合，结果示于图2。

由图2可见，LiCl溶液浓度越高，接收的散射光子数越多，与式（2）的描述一致。但进一步研究发现，由于LiCl的原子序数之和为20，而H2O的原子序数之和为18，原子序数相差不大，理论上散射光子数应不会随LiCl浓度的升高而明显增大，但从实验结果看，拟合的直线斜率很大（散射角为40°和80°的拟合直线的斜率分别为15 985和15 715）。因此，除质量密度、散射衰减因子及溶液的浓度对康普顿散射有影响外，还存在其他因素，因此还应从LiCl溶液的电子结构方面进行深入分析。

图2 康普顿散射相对光子数与浓度的线性关系Fig．2 Relationship between scattered photon count and concentration

3 LiCl溶液电子结构分析

3．1 水分子与离子数之比

一般，对于一定浓度的溶液，存在游离态的离子、游离态的水分子、水合分子、低水合数的水合离子以及高水合数的水合离子，甚至阴阳离子互相进入对方的第一溶剂层，而形成的络合物也同样存在，由于分子、离子等的无规则热运动，它们处于动态平衡中。因此，分析不同浓度溶液的水分子与离子数之比，可估计溶液中游离态的离子、游离态的水分子、水合分子、低水合数的水合离子以及高水合数的水合离子所占的份额。由文献［12］可知，LiCl溶液在标准大气压、20℃下的溶解度为83．5g／100cm2，即饱和溶液浓度为45．5%。此外，不同浓度的溶液中，水分子和离子的个数也可很简单地计算出来（表2）。表2数据表明，随着浓度的升高，低水合数的离子以及游离态的离子越来越多，高水合数的离子越来越少，Li＋和Cl－的水合数在下降。

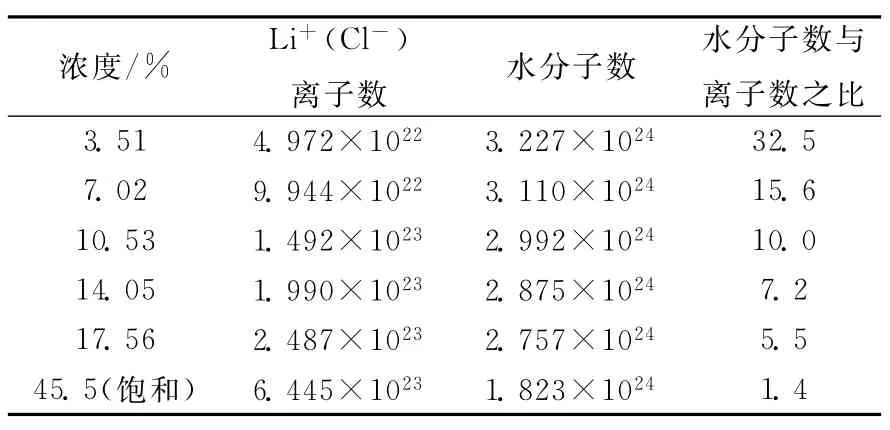
表2 不同浓度LiCl溶液中水分子数与离子数之比（以100g溶液计）Table 2 Ratio between water molecule number and ion number with different concentrations of LiCl solution（in 100g solution）

3．2 优化后LiCl溶液结构

康普顿散射截面体现的是康普顿散射发生的概率，并且文献［13－15］表明，康普顿散射截面受电子束缚程度的影响，而电子受到的束缚程度也会影响康普顿散射的相对光子数。因此讨论散射体LiCl溶液的电子受到的束缚程度，即电子结构具有重要意义。

本文基于密度泛函理论，应用量子化学计算软件Mede A对LiCl溶液的电子结构进行计算，计算中使用拟合电荷的ESP分析法导出电荷分布的相关属性。对于离子和水分子的水合作用，将原子中心电荷拟合至DFT库仑势中。另外，计算中评价能量数据的哈密顿量是dnp，自旋态选用UHF算法，计算精度选择高精度（fine），水作为溶剂，其介电常数为78．4，而对于溶剂化效应COSMO中的其他参数，则采用默认值。

为计算方便，根据表2假定水合数的多少对应于浓度的低高，即浓度高的，其离子的水合数少，浓度低的水合数高。基于此，对水合锂离子和水合氯离子的结构进行优化，结果分别示于图3、4。

图3 优化后水合锂离子的结构Fig．3 Structure of hydrated lithium ion after optimization

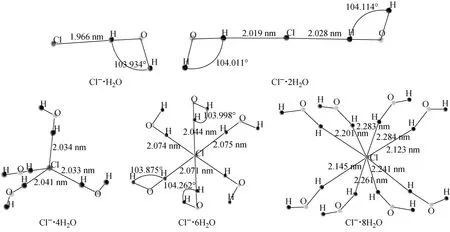
图4 优化后水合氯离子的结构Fig．4 Structure of hydrated chloride ion after optimization

3．3 电子数密度

根据优化后的结构图，计算上述水合离子的电子数密度，结果列于表3。表3中无Cl－· 3H2O和Li＋·8H2O的结果，是由于它们的结构在计算中始终不收敛。有研究［16－18］显示，在稀溶液中Li＋的水合数为4～6，其理论值为4。而对于Cl－·3H2O，由Cl－的核外电子排布可推出，3个水分子只能提供3对孤对电子，既非饱和状态也非半饱和状态。由表2可知，随着浓度的增大，水合Li＋的配位数相对减少，电子数密度减小，而水合Cl—的配位数也相对减少，但其电子数密度增大。相比之下，水合Cl—的电子数密度的增大较Li—的电子数密度的减小更甚，因此总体而言，LiCl浓度的增大导致了电子数密度的增大，这与从原子序数角度考虑的结论相符。即随着浓度的升高，单位体积康普顿散射相对光子数将相应增加，但由于这一增一减的综合效果，这种增加也不会很明显。

表3 水合Li＋和水合Cl－的电子数密度Table 3 Electron number densities of hydrated Li＋and hydrated Cl－

3．4 等效电荷

Li＋和Cl－在水合数不同的情况下其等效电荷（单位为e，指一个电子所带的电荷量）是不同的，具体数据列于表4。

表4 水合Li＋和水合Cl－的等效电荷Table 4 Equivalent charge of hydrated Li＋and hydrated Cl－

由表4可知，Li＋水合数越少（浓度高），其等效电荷越小，电子越偏向Li＋，说明Li＋对电子的束缚就越强，同时也意味着Li＋周围水分子对电子的束缚在减弱；且随着Li＋水合数的减少，水合离子中O的等效电荷绝对值也减小，电子越偏向O，对电子的束缚也减弱，即Li＋浓度越大，电子越自由；而Cl－水合数越少（浓度高），其等效电荷越大，对电子的束缚也越强，说明水合Cl－的电子越不自由。而且随着Cl－水合数的减少，水合离子中O的等效电荷绝对值几乎无变化，表明在水合Cl－中，由于浓度变化，电子对所受到的束缚也发生了变化，从而影响了康普顿散射，在这种影响中，起主要作用的应是Cl－对电子的束缚。Li＋和Cl－对电子束缚的强弱作用的总效果，导致电子的综合自由程度（总体效果看来）基本无变化。根据康普顿散射的量子力学原理，电子受到的束缚越强，发生康普顿散射的概率越小，因此导致接收到的光子数就越少。即仅从LiCl水合离子的等效电荷角度看，随着浓度的升高，康普顿散射相对光子数的变化应不会很明显。

4 结论

选择LiCl溶液作为切入点研究电解质溶液与康普顿散射，从实验上进一步验证了式（2）。

为了解LiCl溶液康普顿散射的微观机理，采用密度泛函理论对Li＋和Cl－水合离子的电子结构进行了深入分析。结果显示，除质量密度、散射衰减因子以及溶液浓度对康普顿散射相对光子数有影响外，电子数密度和电子受到的束缚也对康普顿散射相对光子数有影响。所有这些因素的综合影响导致康普顿散射相对光子数随LiCl溶液浓度的增大而明显增加。

感谢重庆师范大学物理与电子工程学院计算中心的大力支持。

［1］ COMPTON A H．A quantum theory of the scattering of X－rays by light elements［J］．Phys Rev，1923，21（2）：483－502．

［2］ WILLIAMS B．Compton scattering［M］．New York：McGraw－Hill，1977．

［3］ 卢里D．粒子和场［M］．北京：科学出版社，1980．

［4］ RAO D V，SELTZER S M，BERGSTROM P M，Jr．Compton scattering cross－sections for individual subshells for a few elements of biological interest in the energy region 5keV－10MeV［J］．Radiation Physics and Chemistry，2004，70（4－5）：479－489．

［5］ GUIDAL M．Deep virtual Compton scattering and the nucleon generalized parton distributions［J］．Nucl Phys A，2005，751（4）：180－191．

［6］ CLAUDIO C，ANATO R，STERMAN G．QCD sum rules and Compton scattering［J］．Nucl Phys B，1993，405（2－3）：481－506．

［7］ PASQUINUCCI A，PETRINI M．On the Compton scattering in string theory［J］．Phys Lett B，1997，414（3）：288－296．

［8］ HARDING G，HARDING E．Compton scatter imaging：A tool for historical exploration［J］．Applied Radiation and Isotopes，2010，68（1）：993－1 005．

［9］ 罗光，周上祺．康普顿散射法测定溶液浓度［J］．理化检验：化学分册，2010，46（1）：51－53．

LUO Guang，ZHOU Shangqi．Determination of concentration of solutions by the Compton scattering method［J］．Physical Testing and Chemical Analysis：Chemical Analysis，2010，46（1）：51－53（in Chinese）．

［10］LUO G，ZHOU S Q，HAN Z，et al．Relationship between scattered photon counts and concentrations of some saline solutions in Compton scattering［J］．Chin Jour Chem，2007，25（2）：164－167．

［11］HUBBELL J H．Photon cross sections，attenuation coefficients and energy absorption coefficients from 10keV to 100GeV［R］．US：National Standard Reference Data Series，1969．

［12］DEAN J A．Lange’s handbook of chemistry［M］．13th ed．New York：McGraw－Hill，1985．

［13］EAST LV，LEWIS E R．Compton scattering by bound electrons［J］．Physica，1969，11（44）：595－613．

［14］BERGSTROM P M，Jr，SURIC＇T，PISK K，et al．Compton scattering of photons from bound electrons：Full relativistic independent－particleapproximation calculations［J］．Phys Rev A，1993，48（2）：1 134－1 162．

［15］ROLAND R．Relationship of the relativistic Compton cross section to the momentum distribution of bound electron states［J］．Physical Review B，1975，15（12）：2 067－2 074．

［16］BOEK E S，COVENEY P V，SKIPPER N T．Monte Carlo molecular modelling studies of hydrated Li－smectites，Na－smectites，K－smectites：Understanding the role of potassium as a clay swelling inhibitor［J］．J Am Chem Soc，1995，117（50）：12 608－12 617．

［17］PALINKAS G，RADNAI T，HAJDU F．Ionsolvent and solvent solvent interactions：X－ray study of aqueous alkali chorlide solutions［J］．Z Naturforsch A，1980，35（1）：107－114．

［18］MARCHESE F T，BEVERIDGE D L．A pattern recognition approach to the analysis of geometrical features of solvation：Application to the aqueous hydration of Li＋，Na＋，K＋and Cl－［J］．Journal of the American Chemical Society，1984，106（13）：3 713－3 720．

Analysis of Factors Impacting LiCl Solution Compton Scattering

CHEN Kai，LUO Guang＊，CAO Hong－guang，ZHANG Li－peng，CHEN Qing，GUO Hua－qing
（College of Physics and Electronic Engineering，Chongqing Normal University，Chongqing400047，China）

Based on Compton scattering theory，the incoherent scattering attenuation coefficient on the scattering of LiCl solution was discussed．By using some approximations，the expressions of Compton scattering of LiCl solution were obtained，and they are in agreement with the experiments．Then based on the density functional theory，the Compton scattering of LiCl solution was discussed from the microcosmic．The electronic structures of Li＋and Cl－hydration were obtained in LiCl solution．And the factors，electron number density and electron bound strength，impacting LiCl solution Compton scattering photon relative counts were analyzed．The results show that the factors include the electron number density and the electron bound strength，besides the mass density，attenuation coefficient and solution concentration．

Compton scattering；equivalent charge；electron number density；solution structure

O431

A

1000－6931（2015）03－0394－06

10．7538／yzk．2015．49．03．0394

2013－12－20；

2014－06－30

重庆市科委自然科学基金资助项目（CSTC2012jjA50018）；重庆市教委理科科研项目资助（KJ120631）；大学生创新创业训练计划重庆师范大学校级项目资助（201210637036）；重庆市教委重庆高校创新团队项目资助（201013）

陈 凯（1991—），男，江苏南京人，物理学专业

＊通信作者：罗 光，E－mail：photoncn＠cqnu．edu．cn