大跨度钢桁梁铁路斜拉桥刚度参数敏感性分析

李永乐，苏茂材，王士刚，陈克坚

(1.西南交通大学桥梁工程系，成都 610031;2.中铁二院工程集团有限责任公司，成都 610031)

大跨度钢桁梁铁路斜拉桥刚度参数敏感性分析

李永乐1，苏茂材1，王士刚1，陈克坚2

(1.西南交通大学桥梁工程系，成都 610031;2.中铁二院工程集团有限责任公司，成都 610031)

针对某大跨度钢桁梁铁路斜拉桥方案，采用变化结构刚度方法研究梁、索、辅助墩等构件刚度对桥梁结构及行车性能影响。结果表明，增大桁宽能显著增加桥梁横向抗弯刚度，但对车辆走行性影响有限;增加桁高或斜拉索面积能显著提高桥梁竖向基频、降低车桥竖向响应;桥面系对桥梁结构整体刚度贡献不大，对车辆响应影响有限;设置辅助墩可提高斜拉桥竖向刚度、降低车辆竖向加速度及梁端竖向折角等。

铁路斜拉桥;结构刚度;大跨度桥;车桥耦合振动;刚度参数

随我国铁路建设技术的不断发展，桥梁跨度越建越大。中小跨度铁路桥据强度设计的刚度往往较大，通常不控制设计［4］。而大跨度铁路桥梁尤其斜拉桥、悬索桥其刚度问题较突出［1－5］。因此，需分析大跨度铁路桥梁的各结构设计参数，了解影响大跨度铁路桥梁刚度参数及各自在桥梁结构中受力作用。

结构刚度为大跨度斜拉桥设计中重要影响因素。虽有对公路、铁路斜拉桥刚度的研究［2－3］，如竖向刚度［4］、横向刚度［5］、结构阻尼、轨道不平顺、车桥相互作用［6］等，但对铁路斜拉桥刚度参数进行系统研究较有限［4］，对大跨度斜拉桥尤其大跨度纯铁路斜拉桥刚度研究更少见。本文以已建某大跨度双线纯铁路斜拉桥为工程背景，从动力特性及车－桥耦合振动两方面对梁、索、墩等构件刚度对桥梁结构性能影响进行探讨，以期为大跨度铁路斜拉桥设计提供帮助。

1 工程背景

桥梁总体布置见图1，主桥跨度(81+135+432+ 135+81)=864 m，主梁采用平弦等高连续钢桁梁，桥面为正交异性钢桥面板，斜拉索采用双索面预制平行钢丝索。双片桁式主桁桁高14.0 m，采用‘N'形桁，桁宽18.0 m，节间距13.5 m。主梁钢桁梁截面示意图见图2。

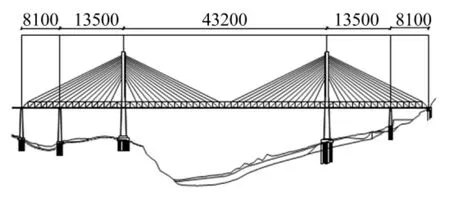
图1 桥梁总体布置图Fig.1 Overall arrangement of bridge

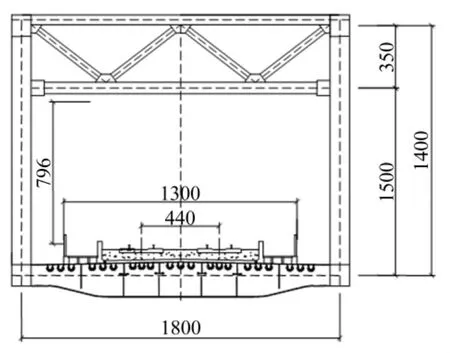
图2 桁架截面(单位:cm)Fig.2 Cross section of truss

2 研究方法

本文从桥梁结构动力特性及车－桥耦合振动两方面研究各构件刚度对桥梁结构性能影响。

2.1 结构动力分析

影响大跨度斜拉桥刚度的因素主要有主梁刚度、斜拉索刚度、辅助墩等。主梁刚度通过桁高、桁宽变化进行研究;跨径、斜拉索距一定时，斜拉索刚度主要取决于面积，因此，将该面积作为斜拉索刚度变化量进行研究;设置辅助墩可改善索梁的锚固链接，通过有、无辅助墩两种工况对比分析其对桥梁整体结构性能影响。

2.2 车－桥系统走行性分析

车－桥系统走行性分析包括考查桁宽、桁高、桥面系、斜拉索刚度、辅助墩、道砟板、二期恒载等因素对桥梁结构动力特性、不同车速下车辆及桥梁动力响应影响。利用车－桥耦合振动模型［7－9］分析列车的走行性。车辆用质点－弹簧－阻尼器模型，桥梁用有限元模型。据位移协调条件及轮轨相互作用力建立耦合关系［9－11］，车辆与桥梁耦合通过车、桥两子系统间分离迭代实现。车－桥系统方程可表示为

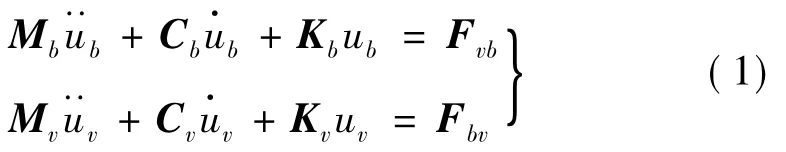
式中:M，C，K分别为质量、阻尼及刚度矩阵;b表示桥梁;v表示车辆;Fvb，Fbv分别为车辆桥梁间相互作用力，其中竖向力及蠕滑力分别用Hertz理论、Kalker线性理论计算。

车－桥系统走行性分析中，车辆、桥梁采用不同敏感性参数。车辆响应中考虑车辆最大加速度，桥梁响应除考虑主跨跨中桥梁最大加速度外亦考虑跨中位移及梁端折角。

3 构件参数敏感性分析

3.1 桁宽敏感性分析

主桁横向设计间距为18 m，分析时取桁宽变化范围9～27 m，分5个工况并考虑斜拉索位置及倾角影响。计算所得各工况下桥梁基频见图3。由图3看出，桥梁扭转基频远大于横向及竖向基频。横向及扭转基频均随桁架宽增大而增大，而竖向基频则略有减小。横弯基频随桁宽增加而增大，说明可通过增大主梁宽度提高横向刚度;但主梁自重会随桁宽增大而增加，竖弯基频会逐渐减小。扭转频率随桁宽增加呈上凸曲线变化，说明适当增加桁宽可提高抗扭刚度，但并非桁架越宽抗扭刚度越大。

对车辆动力响应，计算多种桁宽时各车速下车辆横向、竖向加速度及轮重减载率。由于工况较多，此处只列出部分代表性数据。动车横向加速度随车速、桁宽变化见表1。由表1可知，车辆横向加速度只对车速变化敏感，桁宽影响较有限。

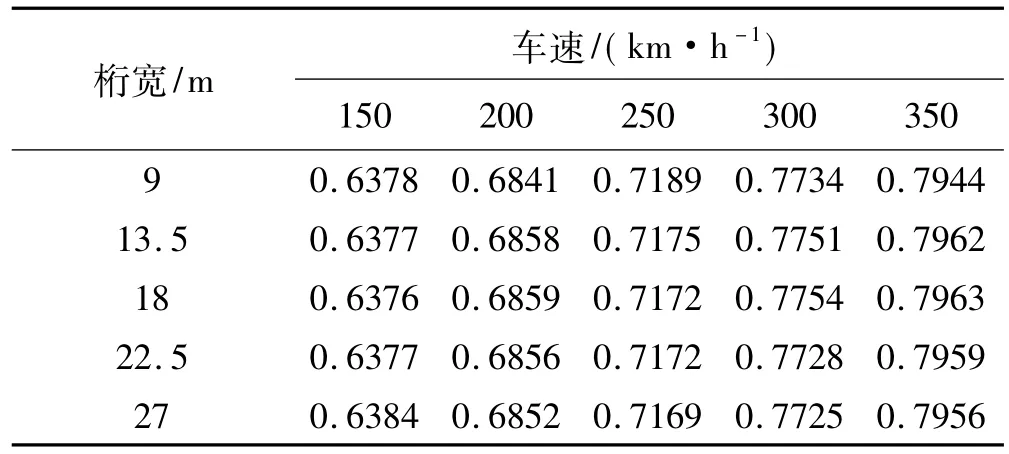
表1 动车横向加速度Tab.1 Lateral acceleration of motor cars

不同车速条件下桥梁跨中横向位移随桁宽变化曲线见图4。由图4看出，桥梁跨中横向位移受桁宽、车速共同作用。桁宽一定时跨中横向位移随车速增加而增加;车速一定时跨中横向位移随桁宽增加而减小，且减小趋势逐渐衰弱;桁宽达到一定值时跨中横向位移趋向于同一值。

3.2 桁高敏感性分析

为考察桁高影响，以设计桁高18 m为中心，每变化3.5 m作为一个工况，共取5个工况进行分析。

结构动力特性随桁高变化见图5。由图5看出，桁高增大时竖弯频率增大、横弯频率减小，两者变化趋势与桁宽增加时相反。扭转频率呈上凸变化，与桁宽变化时扭转频率变化形式一致，即适当增加桁高可提高抗扭刚度，但并非桁架越高抗扭刚度越大。

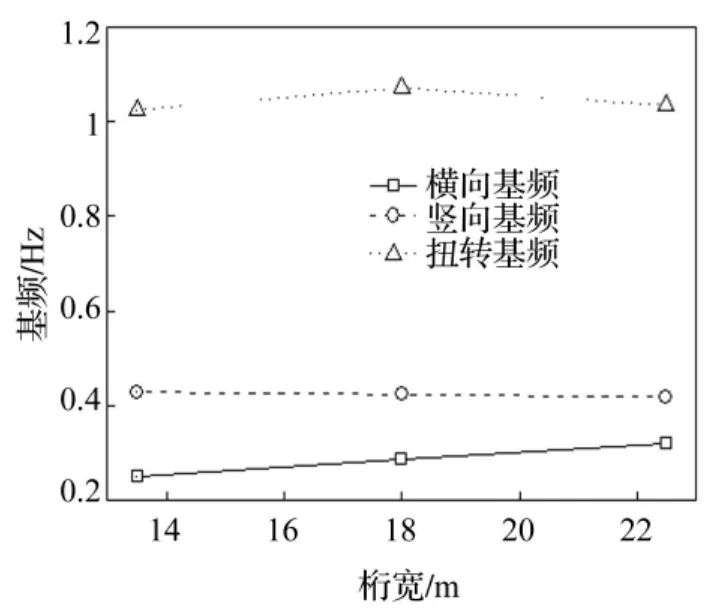
图3 桥梁基频随桁宽变化图Fig.3 Fundamental frequency vs.truss width

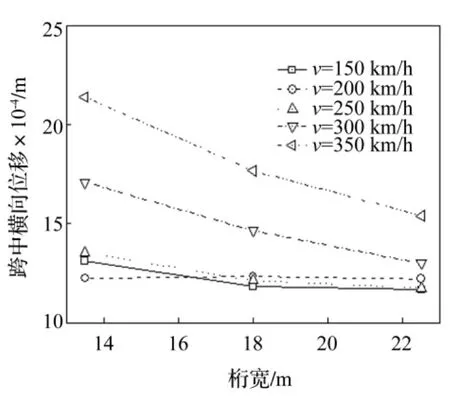
图4 跨中横向位移Fig.4 Lateral displacement at mid－span

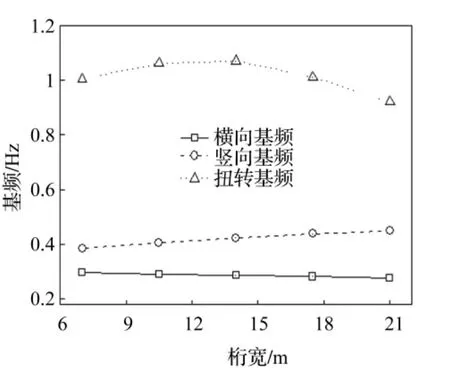
图5 桥梁基频随桁高变化图Fig.5 Fundamental frequency vs.truss height

取不同桁高时各车速下车辆横向、竖向加速度进行分析。结果表明，横向加速度与轮重减载率对桁高变化不敏感，随桁高增加变化较小;竖向加速度对桁高、车速变化较敏感。整体而言，桁高越大竖向加速度越小，车速越大，竖向加速度越大。动车车体竖向加速度随桁高变化见图6。由图6看出，跨中扭转角受车速影响较小，受桁高影响显著，桁高越大扭转角越小;梁端横竖向折角、跨中横竖向加速度、位移皆随桁高增加而减小。

3.3 桥面系敏感性分析

桥面系刚度变化通过改变横梁的弹性模量实现。分析时以原设计弹性模量为基准，每变化25%为一个工况，共计5个工况，其它参数不变。桥梁基频随桥面系刚度变化见图7。由图7可知，桥梁各基频值均无明显变化，说明桥面系刚度变化对桥梁结构整体振动频率影响不大。

与动力特性相对应，桥面系刚度变化对车辆、桥梁动力响应影响均有限，仅跨中扭转角变化较大，见图8。

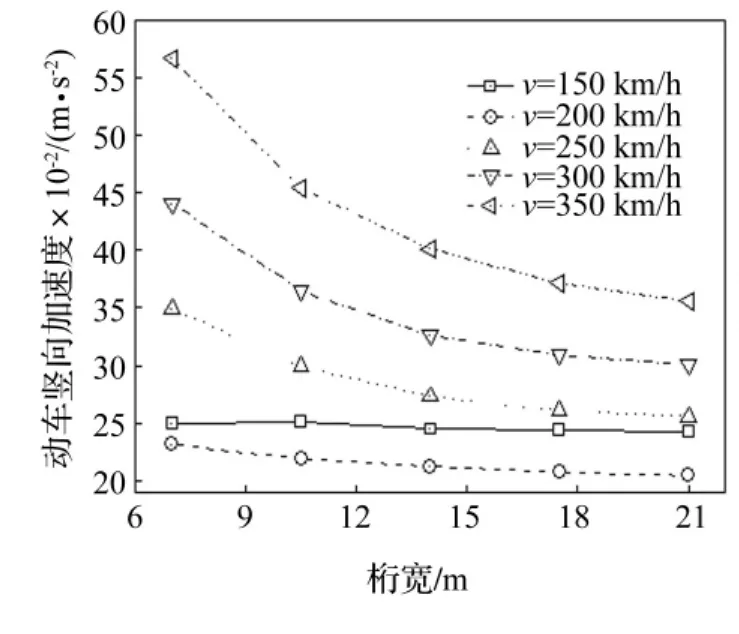
图6 动车竖向加速度Fig.6 Vertical acceleration of motor cars

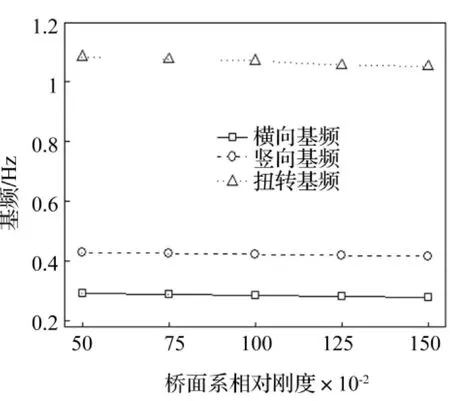
图7 桥梁基频随桥面系刚度变化图Fig.7 Fundamental frequencyvs. bridge deck local stiffness

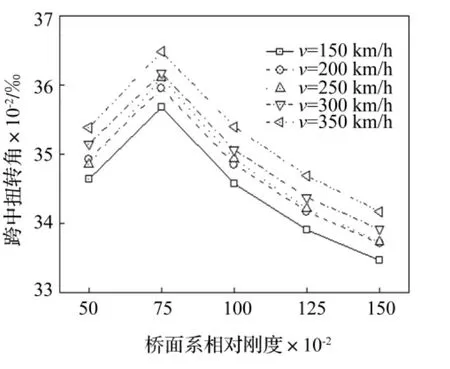
图8 跨中扭转角Fig.8 Torsional angle of midspan

3.4 斜拉索敏感性分析

斜拉索刚度变化通过改变其面积实现。在原设计50%～150%范围分5个工况进行分析，其它参数不变。桥梁基频随斜拉索面积变化见图9。由图9看出，竖弯频率随斜拉索面积增加增大明显，扭转频率略有增加，而横弯频率几乎无变化。在车－桥系统动力响应分析中，车辆、桥梁竖向加速度及位移整体上随拉索刚度增大而减小，而横向加速度及位移等对斜拉索刚度变化不敏感。此因斜拉索平行于主桁面，其刚度变化仅对桥梁竖向参数影响较大。

3.5 辅助墩敏感性分析

通过对比分析有、无辅助墩两种工况下车辆及桥梁响应，研究辅助墩影响。有、无辅助墩的桥梁基频见表2。由表2可见，有辅助墩时桥梁竖弯基频增加明显，即辅助墩可提高桥梁的竖弯刚度。

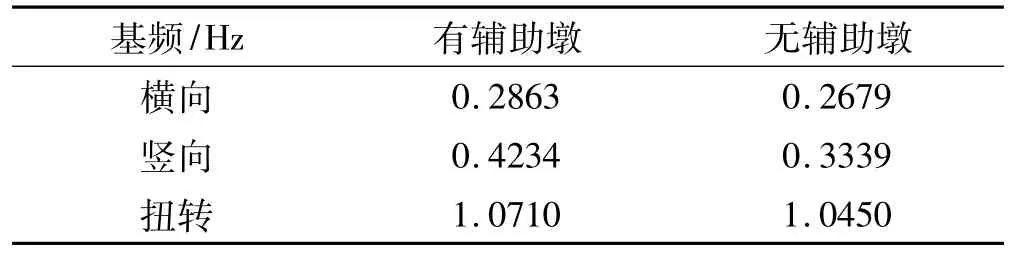
表2 有无辅助墩对桥梁基频影响Tab.2 Effect of auxiliary pier on fundamental frequency

车辆动力响应分析中竖向加速度对桥墩最敏感，增加辅助墩后车辆竖向加速度明显减小，且随车速增加减小趋势越明显，见图10。在桥梁动力响应分析中，梁端竖、横向转角对桥墩最敏感，取消辅助墩后梁端竖向、横向折角均增加约一倍，梁端竖向折角变化见图11。

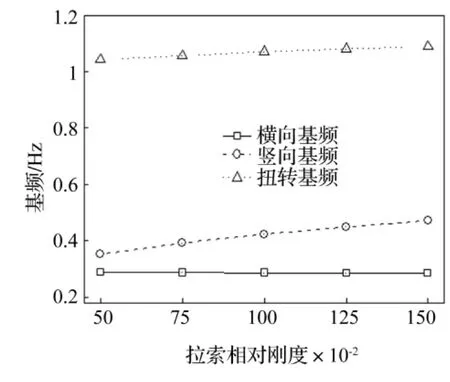
图9 桥梁基频随斜拉索变化图Fig.9 Fundamental frequencyvs. stay cable stiffness

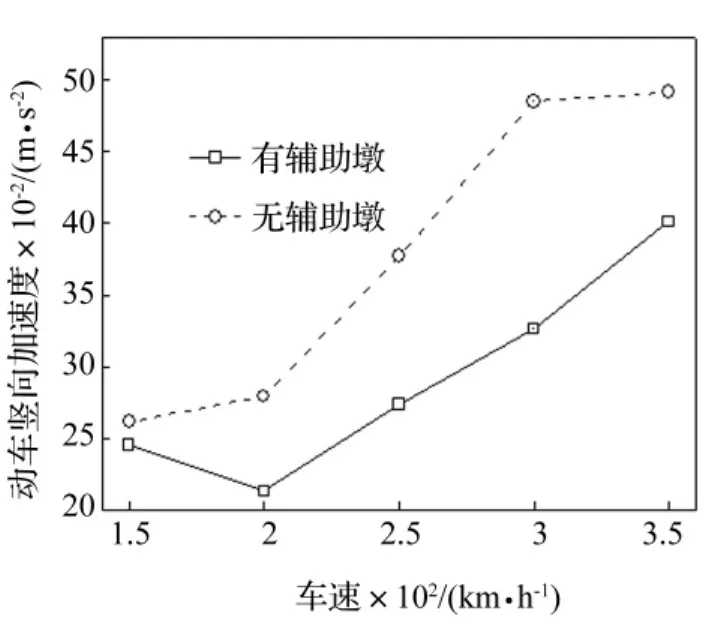
图10 动车竖向加速度Fig.10 Vertical acceleration of motor cars

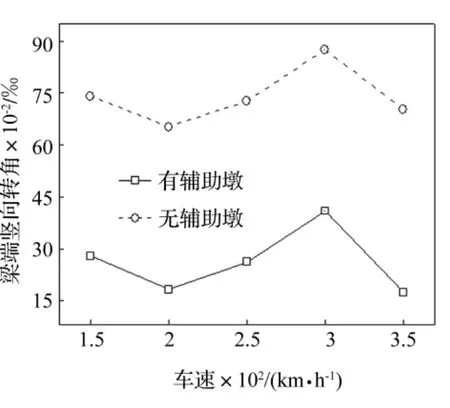
图11 梁端竖向折角Fig.11 Vertical rotation angle at girder end

3.6 道砟板敏感性分析

按道砟板是否参与受力分两种工况进行分析。道砟板与桥面系共同受力时，按等效代换原则，保持换算前后合力、应力大小不变，将混凝土道砟板换算为钢截面。换算前后截面见图12、图13。

图12 铁路桥面系及道砟板截面示意图Fig.12 Railway bridge deck system and ballast board

图13 铁路桥面系及等效道砟板换算截面示意图Fig.13 Transformed section of railway bridge deck system and ballast board

两种情况下桥梁基频见表3。由表3看出，道砟板参与受力前后桥梁横弯、竖弯及扭转基频变化较小，表明道砟板仅影响局部受力，对结构整体行为影响较小。

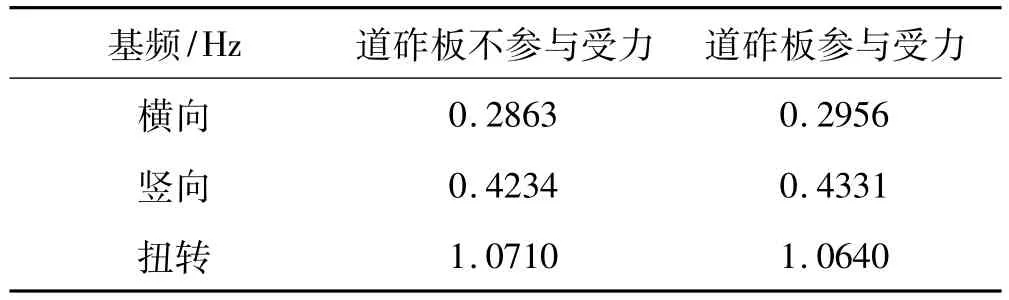
表3 桥梁基频随道砟板影响变化Tab.3 Effect of ballast board on fundamental frequency

与动力特性相似，两种工况下车辆、桥梁各种响应均较接近，道砟板是否参与受力对车－桥系统中车辆、桥梁动力响应影响较小。

3.7 质量敏感性分析

对大跨度铁路斜拉桥而言，二期恒载变化可能会影响结构动力特性，进而影响车－桥耦合响应。因此，虽质量不属于刚度参数，但仍须考虑主梁质量影响。分析质量敏感性时，对比车速200 km/h时二期恒载增加8 t/m及不增加两种工况车辆、桥梁响应，见表4、表5。由两表看出，二期恒载增加8 t/m后车辆响应变化有限，桥梁响应略有差异，差异不大。即二期恒载增加8 t/m对车－桥响应影响有限。

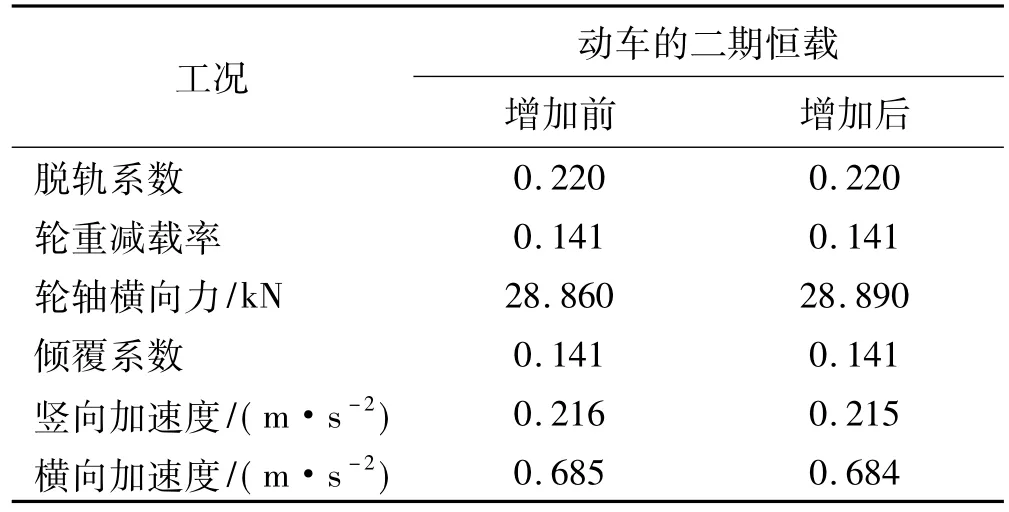
表4 动车响应(CRH2，200 km/h，主桥)Tab.4 Responseof motor cars(CHR2，200 km/h，main bridge)

4 结论

(1)增大桁宽能明显增大桥梁横弯基频，竖弯基频随桁宽增加略有降低，扭转频率随桁宽增加呈先增大后减小趋势。桁宽变化对车辆响应影响有限，对桥梁响应有一定影响。增加桁高桥梁竖向基频相应提高，车桥竖向响应随之下降。扭转频率变化呈先增大后减小趋势。

(2)桥面系对桥梁结构整体刚度贡献不大，板桁桥梁主要为整片主桁共同受力;桥面系不过于柔性时对车桥响应影响有限。

(3)增加斜拉索面积可提高桥梁竖向刚度、减小车辆竖向响应，对桥梁横弯、扭转基频及车辆横向响应影响较小。

(4)辅助墩可显著增加桥梁竖弯基频，降低车辆竖向加速度、跨中竖向挠度及梁端竖向折角。

(5)道砟板是否参与受力对车辆动力响应及桥梁动力响应影响较有限。二期恒载增加8 t/m对车－桥系统响应影响有限。

［1］严国敏.现代斜拉桥［M］.成都:西南交通大学出版社，2000.

［2］张国泉，孙东利.矮塔斜拉桥刚度参数的影响行为［J］.结构工程师，2013，29(1):28－32.

ZHANGGuo－quan，SUNDong－li.Effectsofstiffness parameters onthebehaviorofextradosedbridge［J］. Structural Engineers，2013，29(1):27－32.

［3］曹珊珊，雷俊卿，李忠三，等.多塔斜拉桥刚度分析［J］.世界桥梁，2012，40(1):56－59.

CAO Shan－shan，LEIJun－qing，LIZhong－san，etal. Analysis of rigidity of multi－pylon cable－stayed bridge［J］. World Bridges，2012，40(1):55－59.

［4］程庆国，潘家英.大跨度铁路斜拉桥竖向刚度分析［C］.全国桥梁结构学术大会［A］.武汉，1992:1163－1168.

［5］周智辉，曾庆元，向俊.桥梁横向刚度对列车走行安全性的影响［J］.铁道科学与工程学报，2005，2(2):30－33.

ZHOU Zhi－hui，ZENG Qing－yuan，XIANG Jun.Influence on security of moving train on bridge caused by bridge lateral rigidity［J］.Journal of Railway Science and Engineering，2005，2(2):30－33.

［6］Khalifa MA.Parametricstudyofcable－stayedbridge response due to traffic－induced vibration［J］.Computer＆Structure，1993，47(2):321－339.

［7］Li Yong－le，Qiang Shi－zhong，Liao Hai－li，et al.Dynamics of wind－rail vehicle－bridgesystem［J］.JournalofWind Engineering and Industrial Aerodynamics，2005，93:483－507.

［8］李永乐，蔡宪棠，安伟胜，等.大跨度铁路悬索桥结构刚度敏感性研究［J］.中国铁道科学，2011，32(4):24－30.

LI Yong－le，CAI Xian－tang，AN Wei－sheng，et al.Study on the sensitivity of the structural stiffness of long－span railway suspension bridge［J］.China Railway Science，2011，32(4):24－30.

［9］Marchesiello S，Fasana A，Garibaldi L，et al.Dynamicof multi－span continuous straight bridges subjectto multi－degrees of freedom moving vehicle excitation［J］.Journal of Sound and Vibration，1999，224(3):541－561.

［10］李永乐.风－车－桥系统非线性空间耦合振动研究［D］.成都:西南交通大学，2003.

［11］王归春，潘家英.轨道不平顺导致的车桥耦合振动分析［J］.铁道工程学报，2006，98(8):30－33.

WANG Gui－chun，PAN Jia－ying.Analysis of vehicle－bridge coupled vibration due to track irregularities［J］.Journal of Railway Engineering Society，2006，98(8):30－33.

Sensitivity of structural stiffness parameters of long-span steel truss cable-stayed railway bridge

LI Yong－le1，SU Mao－cai1，WANG Shi－gang1，CHEN Ke－jian2
(1.Department of Bridge Engineering，Southwest JiaotongUniversity，Chengdu 610031，China;
2.China Railway Eryuan Engineering Group Limited Company，Chengdu 610031，China)

Aiming at the design of a long－span cable－stayed railway bridge，the effects of the stiffnesses of girder，cables and auxiliary piers on the bridge structure and the runing performance of vehicles were analyzed.It is shown by the analysis results that the increase of truss width can significantly increase the lateral bending stiffness of the bridge，but has a limited impact on train running performance.Increasing the truss height or cable cross section area can notably increase the fundamental vertical bending frequency and reduce the response of vehicle－bridge systems.Local bridge deck system contributes slightly to the overall bridge stiffness and has a limited impact on the vehicle response.Auxiliary pier can improve the vertical stiffness of the bridge，reduce the vehicle vertical acceleration and the vertical rotation angle at girder ends.

cable－stayed railway bridge;structural stiffness;long span bridge;coupling vibration of vehicle－bridge system;stiffness parameter

U448

A

10.13465/j.cnki.jvs.2015.02.029

国家自然科学基金项目(U1334201);铁道部科技研究计划(2009G004－D)

2013－11－08修改稿收到日期:2014－01－15

李永乐男，博士，教授，博士生导师，1972年生

邮箱:lele@swjtu.edu.cn