悬臂Kagome夹心板独立模态空间振动控制研究

郭空明，江俊

(1.西安电子科技大学机电工程学院，西安 710071;2.西安交通大学机械结构强度与振动国家重点实验室，西安 710049)

悬臂Kagome夹心板独立模态空间振动控制研究

郭空明1，2，江俊2

(1.西安电子科技大学机电工程学院，西安 710071;2.西安交通大学机械结构强度与振动国家重点实验室，西安 710049)

针对悬臂板挠度大、低频振动突出问题，对悬臂Kagome夹心板的振动主动控制进行研究。建立结构及压电作动器有限元模型;将独立模态空间控制与模态观测器相结合，提出悬臂Kagome夹心板的主动控制策略;针对突风载荷作用下夹心板基于独立模态空间的振动控制进行仿真，重点研究观测器极点对控制效果影响。结果表明，所提控制方法能显著提高悬臂Kagome夹心板结构的阻尼特性，观测器衰减系数越大控制效果越好;该夹心板在振动控制方面较传统板结构优势明显。

悬臂板;Kagome夹心板;独立模态空间控制;模态观测器

航空航天领域新材料作用日渐突出。Kagome夹心板［1］作为超轻多孔材料除具有轻质、高比刚度、高比强度等优越性能外，在振动控制方面亦具有明显优越性。普通板结构振动控制一般通过表面粘贴约束层阻尼或压电片实现，不仅影响板面的平整性亦增加质量及厚度。而Kagome夹心板板面被Kagome类型平面桁架代替，通过将一小部分桁架替换成作动器，可实现板面高效变形。因此若将少部分桁架替换为阻尼器或作动器，便可分别实现被动［2］与主动控制［3］。该方法所需作动器、阻尼器数较少，安装方便，且不影响板面形状。

外伸式悬臂薄板为航天航空领域中常见结构。如无人机机翼、卫星太阳能帆板、板状天线等。由于航天航空对重量的限制及此类结构一般无需承受较大载荷致其刚度较低，在受扰动时易引发衰减缓慢的低频振动，需进行减振设计。传统的振动抑制方法有动力吸振［4］、被动控制［5］、主动控制［6］及半主动控制［7］等。动力吸振及半主动控制因会显著增加结构质量而在航空航天领域中应用较少。被动耗能控制对高频振动抑制效果较好，而对低频效果则不佳。故在航天航空领域中，振动主动控制方法逐渐受到重视。

在结构振动中能量往往集中于少数几阶模态，一般为低阶模态。尤其对自由响应而言，由于结构自身阻尼作用，高阶模态振动较快衰减，故在振动主动控制中往往只需控制少数低阶模态。独立模态空间控制［8］(IMSC)即为模态控制方法。该方法计算量小、针对性强且可灵活选择控制律，已成为主动控制的常用方法。因模态坐标无法由传感器直接测得，故IMSC需与模态滤波器［8］或模态观测器［3］结合使用。

本文基于悬臂Kagome夹心板有限元模型，以抑制突风载荷下结构竖向位移、转角为目的，用IMSC对夹心板进行振动控制，以控制力上限最小化为准则对作动器位置进行优化，并着重研究模态观测器增益与控制效果之关系。

1 Kagome夹心板及压电作动器有限元模型

1.1 悬臂Kagome夹心板有限元模型

Kagome夹心板由面板、四面体状夹心层(灰色)及Kagome平面桁架(黑色，桁架在形状、尺寸及材料上完全相同)构成，见图1。

图1 Kagome夹心板示意图Fig.1 Schematic of Kagome sandwich plate

本文研究的Kagome夹心板结构有限元模型见图2。模型由PATRAN建立，面板离散为918个cquad4单元;桁架均用cbar单元，共2 556根，其中Kagome桁架1 278根。板、桁架规格见表1。计算所得前四阶模态固有频率及振型见图3，其中A、B两点为结构响应观测点。由图3看出，悬臂夹芯板固有频率较低，尤其第一阶仅4.9 Hz。第一阶模态振型为一阶弯曲，第二阶模态振型为一阶扭转，三、四阶模态为高阶弯曲与弯扭组合。由于结构振动频率较低，适合用主动振动控制方法。

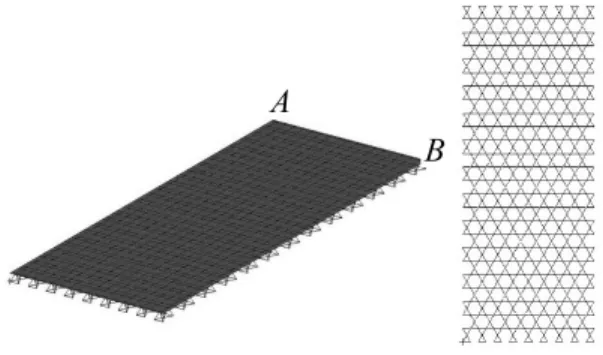
图2 悬臂Kagome夹芯板及Kagome平面桁架有限元模型Fig.2 Finite element models of cantilever Kagome sandwich plate and Kagome planar truss

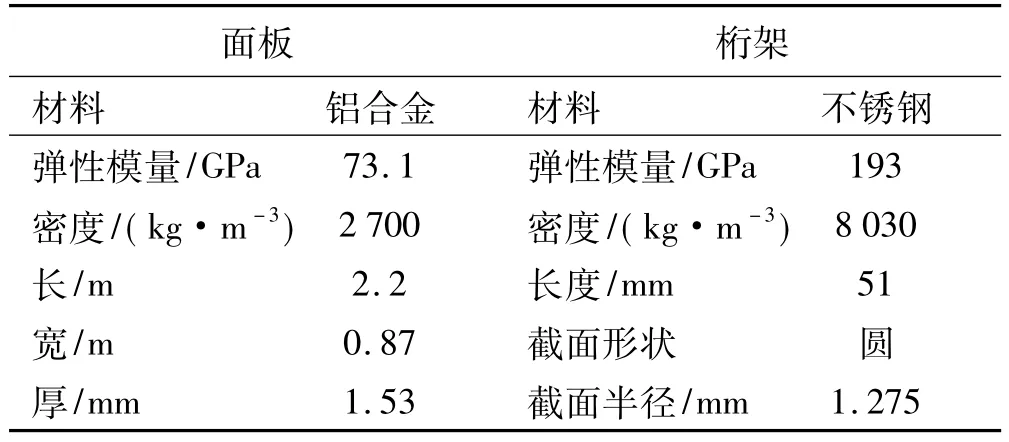
表1 面板、桁架材料及尺寸Tab.1 Material parameters and size of face sheet and truss rods

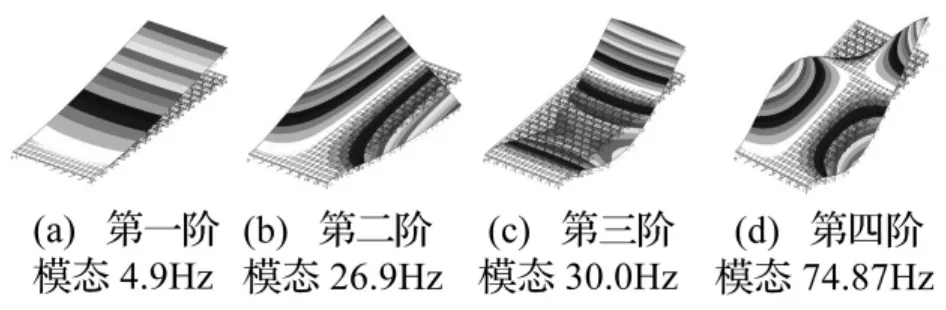
图3 悬臂Kagome夹心板1～4阶模态固有频率及振型Fig.3 Natural frequencies and modal shapes of mode 1～4 of cantilever Kagome plate

1.2 压电作动器有限元模型

本文用压电作动器进行主动控制。忽略压电单元自感应电场。压电堆动力学方程［9］为

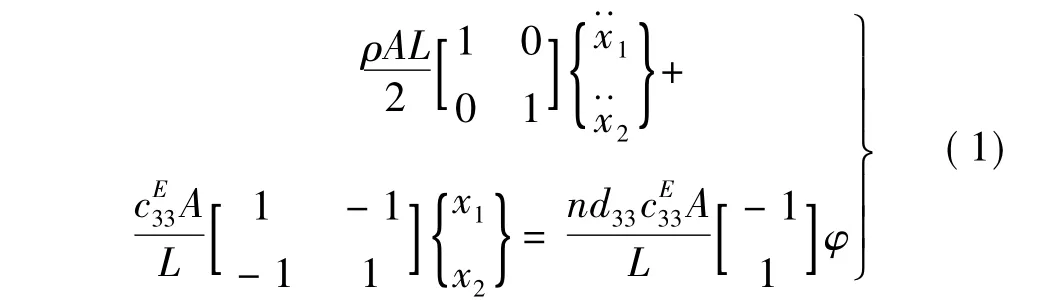
式中:ρ为压电堆密度;A为压电堆截面积;L为压电堆总长;x1，x2为压电堆两端点位移;cE33为常电场E作用下压电堆轴向弹性模量;n为压电堆所含压电片个数;d33为压电应变系数;φ为压电片两端电势差。

压电作动器结构见图4。其中预压弹簧可使压电堆处于受压状态，使作动器既可产生推力也可产生拉力;球铰用于防止压电堆受到弯曲、扭转作用。

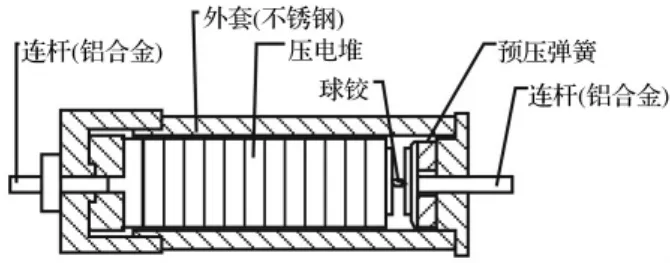
图4 压电作动器示意图Fig.4 Sketch of the piezoelectric actuator

结合连杆和及压电堆有限元模型，并凝聚掉内部自由度，得压电作动器在局部坐标下的有限元模型为

式中:［Me］为质量矩阵;［Ke］为刚度矩阵;［Kce］为位移变量与电势变量耦合矩阵;{qe}为位移向量;φ为电势变量。矩阵［Me］，［Ke］，［Kce］表达式为

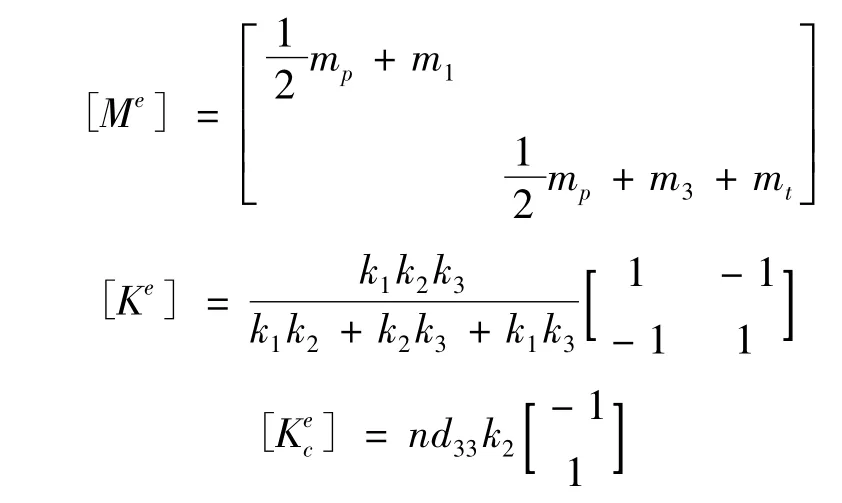
式中:k1，k3为两连杆刚度;k2为压电堆、外套及预压弹簧等效刚度;mp为压电堆质量;m1，m3为两连杆质量;mt为外套及预压弹簧总质量。其它部件质量较小，可忽略。

在设计尺寸下作动器轴向刚度与原杆件轴向刚度基本一致，替换作动器几乎不对结构动力学特性产生影响。当外加电压为V时φ=－V，作动器作动力为

2 振动主动控制方案

2.1 独立模态空间控制

不考虑外部载荷，含作动器的结构方程为

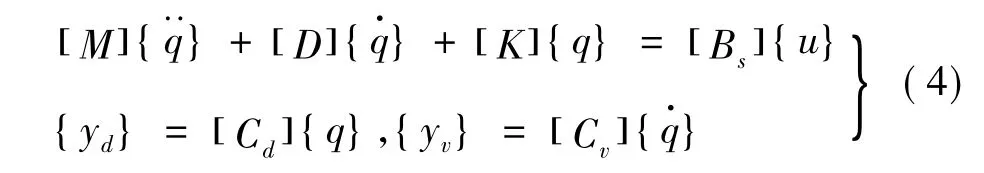
式中:{q}为节点位移向量;{q·}为速度向量;{q··}为加速度向量;［M］为质量矩阵;［D］为阻尼矩阵;［K］为刚度矩阵;［Bs］为作动器空间耦合矩阵;{u}为控制力向量;{yd}为位移观测向量;{yv}为速度观测向量;［Cd］为位移观测矩阵;［Cv］为速度观测矩阵。

IMSC所需作动器及传感器数目相等，均等于需控制的模态数。将全部模态分为控制模态与剩余模态两类，下标c，r分别对应控制模态、剩余模态。设［ψ］为系统模态矩阵，含控制模态［ψc］及剩余模态［ψr］两部分，令

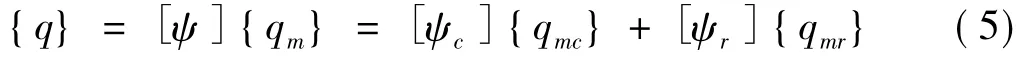
式中:{qm}为模态位移向量，含控制模态{qmc}及剩余模态{qmr}两部分。

将式(5)代入式(4)，用［ψ］T左乘式(4)第一方程，得

在IMSC中据模态位移、速度求得所需模态控制力向量{fc}，再求出物理控制力向量{u}。设控制模态数为n，则式(8)含n个由控制模态组成的独立方程，第i阶模态方程为

2.2 模态观测器

一般情况下，模态坐标下位移、速度等无法直接测得。因此需能估计模态坐标的观测器。对自由度较多的结构，只选所需控制模态进行观测。为此，将式(6)控制模态部分写成状态空间形式为

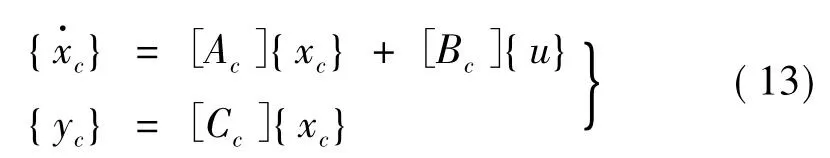
式中:［Ac］为系统矩阵;［Bc］为输入矩阵;［Cc］为输出

矩阵;{xc}为控制部分状态向量，形式有

式中:［P］为Riccati方程的解;［W］为系统噪声的协方差矩阵;［V］为测量噪声的协方差矩阵。观测器增益矩阵［Hc］为

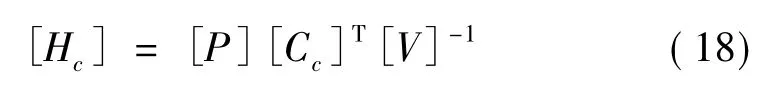
由于模态观测器未考虑剩余模态，可能造成控制模态阻尼比增加时剩余模态阻尼比反而减小，该现象称为溢出。若某阶剩余模态阻尼比降为负值，系统会不稳定。为分析主动控制作用下系统的稳定性，定义观测器的误差向量为

闭环矩阵所有特征值实部均为负值时系统才是稳定的。矩阵中［Hc］［Cr］使传感器输出中带有剩余模态的量，称为观测溢出。同时，剩余模态通过［B］［G］对剩余模态进行激励，称为控制溢出。模态观测器即为减少观测输出中剩余模态分量，通过设计观测器增益矩阵将其作为观测噪声过滤掉。

为进一步减少观测输出中剩余模态分量，重写式(17)、(18)［10］为

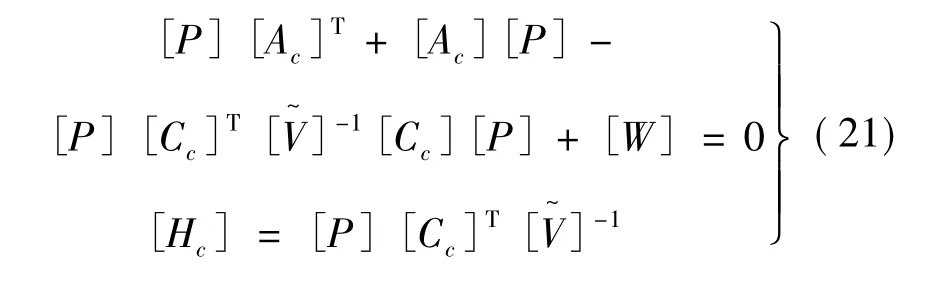
3 突风载荷下悬臂Kagome夹心板振动控制

3.1 突风载荷及结构响应

考虑Kagome夹心板作为机翼受突风扰动，设突风载荷垂直于板面并沿展向均匀分布。飞行器受扰运动只有竖直方向自由度z，以飞行器质心为准，以向下为正。运动方程［11］为

式中:M为飞行器质量;LG为突风引起的总升力，计算公式为

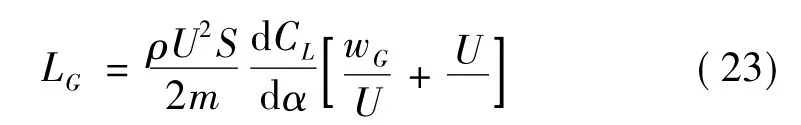
式中:ρ为空气密度;S为机翼表面积;U为飞行速度; CL为升力系数;α为攻角;wG为突风速度。

将式(23)代入式(22)得

设突风载荷作用于1/4弦长处，对结构进行突风响应模拟，重点观察悬臂板竖向位移及扭转。观测点为图1中A、B两点，其中A点为竖向位移观测点。无量纲扭转角φ的计算式为

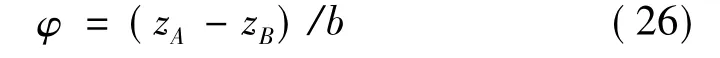
式中:zA，zB分别为A、B两点竖向位移;b为悬臂板宽度。

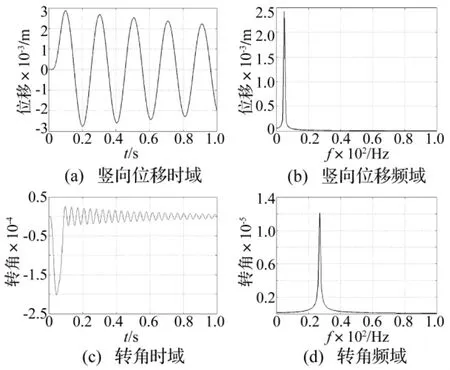
图5 突风载荷下竖向位移及转角的响应Fig.5 Responses of vertical displacement and angle of rotation under gust load

对暂态激励，高阶模态频衰减较快，且加速度传感器带宽有限，无法测得一定范围外的高阶信号，不考虑此模态引发的溢出。因此可采用模态截断方法进行时域计算。设传感器截止频率约1 000 Hz，取前200阶模态(最高频率1 030 Hz)，模态阻尼比取1%。计算获得竖向位移及转角的时、频域响应见图5。由图5看出，位移、转角衰减较慢，尤其位移，由于振动频率较低，1 s后仍未充分衰减。

3.2 控制效果

由图5知，位移、转角分别以第一、二阶模态为主，故用IMSC对两阶模态进行控制，所需作动器数目、传感器数目为2。需替换两根桁架作为作动器，占Kagome平面桁架的0.16%，桁架总数的0.08%。通过作动器合理优化布置，可在给定模态作动力前提下使所需物理作动力尽量小。因此用作动器优化方法［2］使作动力上限尽量小。优化目标为使矩阵［Bmc］的最小奇异值σmin最大化，即

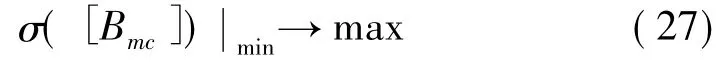
因只需确定两根作动器位置，组合优化问题计算量较小，可用遍历方法取得最优解。传感器位置由每阶模态中z向位移最大节点确定。作动器、传感器位置见图6中粗实线及三角形。所用电容式三轴加速度传感器体积小、重量轻，布置于Kagome桁架连结点。对所测加速度积分便可获得节点速度及位移。由于系统频率较低，为使结构振动尽快衰减，取前两阶模态期望达到模态阻尼比为7.5%。

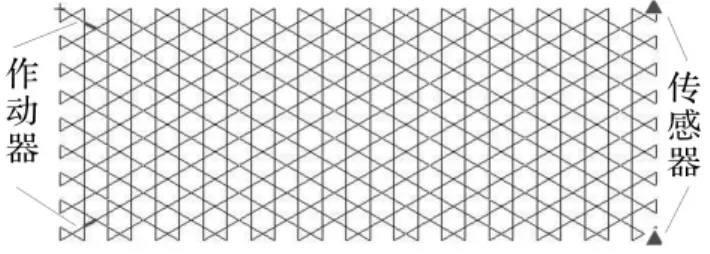
图6 作动器和传感器的位置Fig.6 Placements of actuators and sensors

式(21)中，［V］可抑制观测输出中剩余模态成分。［V］越大抑制效果越好，但也会使观测器收敛速度变慢。因此就观测器对控制效果影响进行研究。固定［W］=［I］，分别取［V］=［I］，5［I］，10［I］，20［I］，其中［I］为单位矩阵，获得不同观测器增益矩阵［Hc］。对闭环系统进行特征值分析，在复平面绘制各情况下观测器一对闭环极点，见图7。由图7看出，［V］越小，复平面观测器极点越靠左，误差衰减越快。

为考察观测器极点对控制效果影响，计算四种权矩阵及未施加控制时五种情况的位移、转角时间历程，见图8。由于转角振动频率较高，为便于观察，取小的时间范围。由图8看出，主动控制效果非常明显，较未控制状态，位移、转角衰减速度均有较大提高。

计算获得四种控制情况下真实响应衰减速率及模态阻尼比。［V］=［I］，5［I］，10［I］，20［I］时第一阶模态阻尼比分别为7.48%、6.68%、5.86%、4.88%，第二阶模态阻尼比分别为7.31%、7.06%、6.75%、6.09%。由于观测误差衰减速率为有限值，因此模态阻尼比不能精确达到设计的7.5%;而权矩阵［V］越小，观测器极点越靠近复平面左侧，误差衰减越快，所达真实模态阻尼比越接近设计值。因此，在保证无控制溢出前提下，应尽量提高观测器衰减速率。

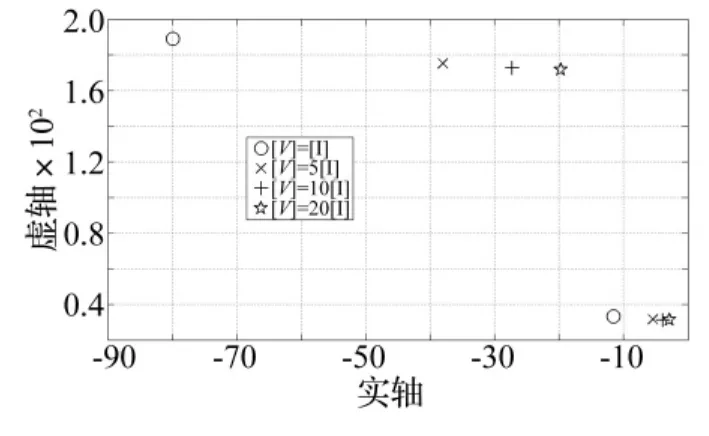
图7 不同权矩阵时观测器极点比较Fig.7 Comparison of observer poles using different weighting matrices

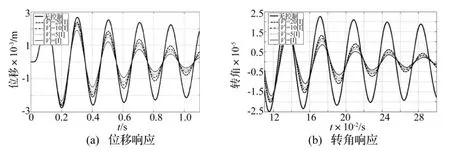
图8 五种情况下位移、转角响应Fig.8 Responses of displacement and angle of rotation in five cases

4 结论

针对航空航天领域中悬臂结构振动问题，本文引入新材料—Kagome夹心板结构实施振动主动控制。对突风载荷作用的悬臂Kagome夹心板结构用IMSC方法，以控制力上限最小化为目标，利用作动器实现对结构前两阶模态振动控制。结论如下:

(1)对悬臂Kagome夹心板用IMSC进行主动控制，只需用作动器替换结构中极少桁架杆，便会有较好的振动控制效果。

(2)观测器误差收敛速度会影响实际达到的模态阻尼比，在保证闭环稳定性前提下应使观测器收敛速度尽量加快。

(3)由于作动器布置于Kagome平面桁架，不会影响面板形状及厚度。对易产生低频振动的悬臂板结构，Kagome夹心板应用前景较好。

(4)通过研究观测器增益与控制效果之关系知，权矩阵越小误差衰减越快，真实模态阻尼比越接近设计值。应在保证无控制溢出前提下尽量提高观测器衰减速率。

［1］Wicks N，Hutchinson J W.Sandwich plates actuated by a Kagomeplanartruss［J］.ASMEJournalofApplied Mechanics，2004，71(5):652－662.

［2］Guo X，Jiang J.Passive vibration control of truss－coredsandwich plate with planar Kagome truss as one face plane［J］.ScienceinChina－TechnologicalScience，2011，54(5):1113－1120.

［3］Guo X，Jiang J.Optimization of actuator placement in a trusscored sandwich plate with independent modal space control［J］.Smart Materials and Structures，2011，20(11):115011.

［4］杨飞，杨智春，王巍.吸振夹层壁板颤振抑制的吸振器频率设计［J］.振动与冲击，2009，28(7):65－68.

YANG Fei，YANG Zhi－chun，WANG Wei.Frequency design of dynamic vibration absorbers for flutter suppression of a sandwich panel［J］.Journal of Vibration and Shock，2009，28(7):65－68.

［5］徐赵东.粘弹性减震控制结构随机状态反应分析［J］.振动与冲击，2008，27(1):37－39.

XU Zhao－dong.Randomstateresponseanalysisfora viscoelastic earthquake－mitigating structure［J］.Journal of Vibration and Shock，2008，27(1):37－39.

［6］董兴建，孟光.压电悬臂梁的动力学建模与振动主动控制［J］.振动与冲击，2005，24(6):54－64.

DONG Xing－jian，MENG Guang.Dynamics modeling and active vibration control of cantilever beam with piezoelectrics［J］.Journal of Vibration and Shock，2005，24(6):54－64.

［7］刘永强，杨绍普，申永军.基于磁流变阻尼器的汽车悬架半主动相对控制［J］.振动与冲击，2008，27(2):154－161.

LIU Yong－qiang，YANG Shao－pu，SHEN Yong－jun.Semiactive relative control schemes for vehicle suspension using a magnetorheological damper［J］.Journal of Vibration and Shock，2008，27(2):154－161.

［8］卢连成，吴琼，张令弥.智能空间桁架结构独立模态控制方法［J］.振动工程学报，1997，10(4):480－485.

LU Lian－cheng，WU Qiong，ZHANG Ling－mi.Modal filter control method for intelligent space truss structures［J］. Journal of Vibration Engineering，1997，10(4):480－485.

［9］李东旭.大型挠性空间桁架结构动力学分析与模糊振动控制［M］.北京:科学出版社，2008.

［10］Preumont A.Vibration control of active structures:an introduction［M］.Berlin:Springer，2002.

［11］Chattopadhyay A，Seeley D E，Jha R.Aeroelastic tailoring using piezoelectric actuation and hybrid optimization［J］. Smart Materials and Structures，1999，8(1):83－91.

Independent modal space vibration control of cantilever Kagome sandwich plate

GUO Kong－ming1，2，JIANG Jun2
(1.School of Electronic and Mechanical Engineering，Xidian University，Xi＇an 710071，China;
2.State Key Laboratory for Strength and Vibration of Mechanical Structures，Xi＇an Jiaotong University，Xi＇an 710049，China)

Active vibration of a kind of cantilever Kagome sandwich plate was studied.A finite element model of the cantilever structure with piezoelectric actuator was established.An active control strategy for cantilever Kagome sandwich plate was proposed by combining the independent modal space control with a modal observer.Aiming at one kind of gust load，the independent modal space control of Kagome sandwich plate was simulated，while the influence of observer poles on the control effect was focused on.The results show that the control method can significantly improve the damping properties，and a greater attenuation factor of the observer can get better control effect.Therefore，Kagome sandwich panel has obvious advantages over traditional board structure in vibration control aspect.

cantilever plate;Kagome sandwich plate;independent modal space control;modal observer

O328;V214.3

A

10.13465/j.cnki.jvs.2015.02.010

中央高校基本科研业务费专项资金项目(K5051304012)

2013－11－08修改稿收到日期:2014－01－15

郭空明男，博士，讲师，1985年生